A Lightweight Denoising-Enabled Pre-trained Model-Based Retrieval-Augmented Generation Pipeline

چکیده فارسی

در سیستم‌های دستیار هوشمند که از معماری تولید تقویت‌شده با بازیابی استفاده می‌کنند، وجود نویز در داده‌های متنی ورودی (مانند متون غیررسمی، مختصر یا دارای اشتباه) به‌طور مستقیم بر دقت بازیابی اطلاعات و در نتیجه، کیفیت پاسخ نهایی تأثیر منفی می‌گذارد. این پژوهش، یک پایپ‌لاین سبک‌وزن و عملی را معرفی می‌کند که هدف آن، افزایش مقاومت این دستیارها در برابر نویز است.

روش پیشنهادی بر سه پایه اصلی استوار است: نخست، از یک مدل ازپیش‌آموزش‌دیده و بهینه برای استخراج بازنمایی معنایی از متون استفاده می‌شود. سپس، یک لایه پروجکشن به‌صورت یک گام پردازشی افزوده می‌گردد که بازنمایی‌های استخراج‌شده را به یک زیرفضای معنایی کم‌بعدتر و عاری از نویز تبدیل می‌کند. این فرآیند پروجکشن، مؤلفه‌های کم‌اهمیت و پرنویز داده را حذف می‌نماید. در نهایت، بازنمایی‌های «تمیز» شده برای ایندکس‌سازی و بازیابی سریع در یک پایگاه داده برداری ذخیره می‌شوند.

ارزیابی این پایپ‌لاین بر روی یک مجموعه داده شبه‌واقعی حاوی متون پُرنویز نشان می‌دهد که این معماری ساده و مبتنی بر مدل‌های موجود، نه تنها نیاز به منابع سخت‌افزاری سنگین را مرتفع می‌سازد، بلکه به‌طور قابل‌توجهی منجر به بازیابی مرتبط‌تر اسناد و در نتیجه تولید پاسخ‌های دقیق‌تر توسط مدل زبانی بزرگ در مقایسه با پایپ‌لاین‌های سنتی می‌شود. این پایان‌نامه مسیری مقرون‌به‌صرفه و کارآمد برای توسعه دستیارهای هوشمند مقاوم در محیط‌های عملیاتی را ارائه می‌نماید.

مقدمات مورد نیاز

ابتدا مفهوم نویززدایی مبتنی بر پروجکشن، با معرفی انواع ابزار همچون PCA, SVD بررسی می شود و سپس به معرفی مدلهای از پیش اموزش دیده پرداخته می شود که توانایی تبدیل متن، تصویر، ویدیو و صوت را دارند ، ارایه می گردد. . نهایتا مرور بر ادبیات در زمینه مورد بحث یک تولید تقویت شده، ارایه می شود.

تحلیل مؤلفه‌های اصلی (PCA)

این متن از این ادرس و مراجع دیگر استفاده شده است

Principle Component Analysis

در پردازش سیگنال در موارد زیادی سیگنالهایی با تعداد ویژگی زیاد مواجه هستیم. همچون

ابعاد بالا دارای ویژگی‌های زیادی هستند مانند سیگنال‌های EEG از مغز یا رسانه‌های اجتماعی و غیره. تصاویر نیز امروزه یک داده با ویژگی زیاد و بسیار مورد استفاده در سیستمهای یادگیر است و پردازش متن که یکی از جاذبه های هوش مصنوعی است یکی دیگر از نمونه های ویژگی زیاد می توان نام برد

برخی از مزایای کاهش ابعاد

مصورسازی
کمک به جلوگیری از بیش‌برازش
استفاده کارآمدتر از منابع
پردازش ساده تر
کاهش اثر نویز و بررسی مولفه های اصلی

در تصویر زیر راستای با کشیدگی بیشتر را مولفه اصلی و راستای با کشیدگی کمتر را ناشی از نویز تلقی می کنیم این موضوع اساس کار روش مولفه های اصلی است که با نام pca معروف است

تکنیک‌های کاهش ابعاد

۱. انتخاب ویژگی (Feature Selection)

تعریف ریاضی

انتخاب زیرمجموعه‌ای به اندازه $k$ از $d$ ویژگی اصلی ($k \ll d$) با استفاده از یک نگاشت گزینشی.

مدل ریاضی

ورودی:
- ماتریس داده اصلی: $\mathbf{X} \in \mathbb{R}^{n \times d}$
- بردار انتخاب: $\mathbf{m} \in {0,1}^d$ به طوری که $\sum_{j=1}^d m_j = k$
تبدیل: $\mathbf{X}_{\text{filtered}} = \mathbf{X} \cdot \text{diag}(\mathbf{m})$ $\text{diag}(\mathbf{m}) = \begin{bmatrix} m_1 & 0 & \cdots & 0 \\ 0 & m_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & m_d \end{bmatrix}$
خروجی: $\mathbf{X}{\text{selected}} \in \mathbb{R}^{n \times k}$ (حاصل حذف ستون‌های صفر از $\mathbf{X}{\text{filtered}}$)

تفسیر

این فرآیند معادل یک پروجکشن خطی گزینشی به زیرفضایی $k$-بعدی است که ویژگی‌های با واریانس-نویز پایین را حفظ می‌کند.

۲. استخراج ویژگی (Feature Extraction)

تعریف ریاضی

یک تبدیل از فضای ویژگی اصلی

\[\mathbb{R}^d$ به فضای کم‌بعد $\mathbb{R}^k\] \[\phi: \mathbb{R}^d \to \mathbb{R}^k\]

الف) استخراج خطی

\[\mathbf{Z} = \mathbf{X} \mathbf{W}\]

ماتریس تبدیل پروجکشن

\[\mathbf{W} \in \mathbb{R}^{d \times k}\]

داده در فضای جدید $\mathbf{Z} \in \mathbb{R}^{n \times k}$

ب) استخراج غیرخطی

\[\mathbf{z}_i = \phi(\mathbf{x}_i), \quad \forall i \in \{1, \dots, n\}\]

نمونه الگوریتم‌ها

| روش | نوع | تابع تبدیل | |—–|—–|————-| | PCA | خطی | $\mathbf{W}{\text{PCA}} = \arg\min{\mathbf{W}^T\mathbf{W}=\mathbf{I}} |\mathbf{X} - \mathbf{X}\mathbf{W}\mathbf{W}^T|F^2$ | | Autoencoder | غیرخطی | $\phi = \psi \circ \varphi$ (کدگذار-کدگشا) | | Kernel PCA | غیرخطی | $\phi(\mathbf{x}) = \sum{i=1}^n \alpha_i k(\mathbf{x}_i, \mathbf{x})$ |

نکته مهم: در کاهش نویز مبتنی بر این نوع پروجکشن ها نویز را در اجتماعی از داده ها کم می کنند بعبارتی داده های رسیده همچون شکل زیر بما خواهند گفت کدام ویژگیها مهم برای نگهداری و کدامها بهتر از حذف شوند و این ایده پروجکشن را خواهد ساخت

denoising_in_crowd1 — *حذف نویز در جمع داده ها*

در ادامه درک مفهوم محور اصلی و ریاضیات و برنامه نویسی PCA را می فهمیم

کد: مجموعه داده گوسی 2 بعدی

این کد پایتون داده‌های 2 بعدی را از یک توزیع نرمال چندمتغیره با میانگین و ماتریس کوواریانس زیر تولید و مصورسازی می‌کند:

بردار میانگین:

\[\mu = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\]

ماتریس کوواریانس:

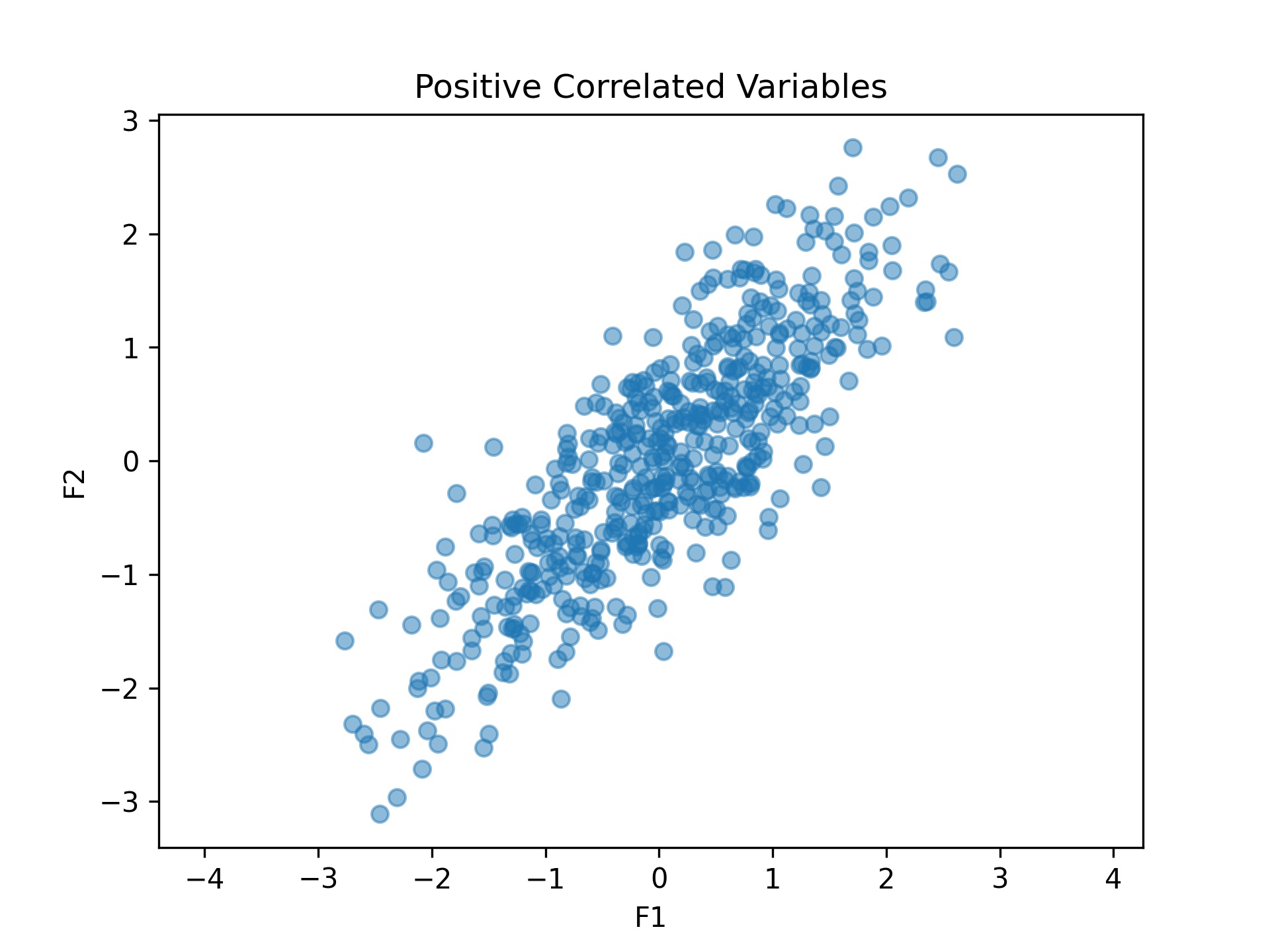
\[\Sigma = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1 \end{bmatrix}\]

این کد یک نمودار پراکندگی از 1000 نمونه ایجاد می‌کند که همبستگی بین دو متغیر را نشان می‌دهد، با نسبت ابعاد برابر و شبکه برای وضوح بیشتر.

import numpy as np
import matplotlib.pyplot as plt

# تعریف بردار میانگین و ماتریس کوواریانس
mean = [0, 0]  # مثال: داده 2 بعدی با میانگین صفر
cov = [[1, 0.8], [0.8, 1]]  # ماتریس کوواریانس (2x2)

# تعداد نمونه‌ها
n_samples = 1000

# تولید داده
data = np.random.multivariate_normal(mean, cov, size=n_samples)

plt.scatter(data[:,0], data[:,1])
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("داده‌های پراکنده")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.legend()
plt.grid(True)
plt.show()

کد: اولین محور PCA

این کد پایتون ماتریس کوواریانس داده‌های تولید شده را محاسبه می‌کند، تجزیه ویژه را انجام می‌دهد و اولین محور اصلی (بردار ویژه با بزرگترین مقدار ویژه) را مصورسازی می‌کند. نمودار نقاط داده را به همراه اولین محور اصلی نشان می‌دهد که با یک پیکان قرمز نشان داده شده است و جهت بیشینه واریانس در داده‌ها را نشان می‌دهد. محور برای مصورسازی بهتر مقیاس‌دهی شده است و نمودار شامل خطوط شبکه، برچسب‌های محور و یک راهنما است.

# محاسبه ماتریس کوواریانس داده‌های تولید شده
data_cov = np.cov(data, rowvar=False)

# انجام تجزیه ویژه
eigenvalues, eigenvectors = np.linalg.eigh(data_cov)

# یافتن اولین محور اصلی (بردار ویژه با بزرگترین مقدار ویژه)
first_principal_axis = eigenvectors[:, np.argmax(eigenvalues)]

# مقیاس‌دهی محور برای مصورسازی
scaling_factor = 2  # فاکتور مقیاس دلخواه برای مصورسازی بهتر
axis_line = first_principal_axis * scaling_factor

# رسم داده‌ها
plt.figure(figsize=(6, 6))
plt.scatter(data[:, 0], data[:, 1], alpha=0.5, s=10, label="داده")
plt.axhline(0, color="gray", linestyle="--", linewidth=0.8)
plt.axvline(0, color="gray", linestyle="--", linewidth=0.8)

# افزودن اولین محور اصلی
plt.quiver(
    mean[0], mean[1], 
    axis_line[0], axis_line[1],
    angles="xy", scale_units="xy", scale=1, color="red", label="اولین محور اصلی"
)

# افزودن برچسب‌ها و عنوان
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("نمودار پراکنده با اولین محور اصلی")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.legend()
plt.grid(True)
plt.show()

کد: محور اول و دوم

این کد پایتون ماتریس کوواریانس داده‌های تولید شده را محاسبه می‌کند و تجزیه ویژه را برای استخراج دو مؤلفه اصلی اول انجام می‌دهد. مؤلفه‌های اصلی برای مصورسازی بهتر مقیاس‌دهی شده و در کنار داده‌ها رسم می‌شوند. مؤلفه اصلی اول (بزرگترین مقدار ویژه) به رنگ قرمز و مؤلفه اصلی دوم (کوچکترین مقدار ویژه) به رنگ آبی نشان داده می‌شود. نمودار شامل خطوط شبکه، برچسب‌های محور و یک راهنما است، با نسبت ابعاد برابر تا جهت‌گیری مؤلفه‌های اصلی در رابطه با داده‌ها به وضوح مصورسازی شود.

# محاسبه ماتریس کوواریانس داده‌های تولید شده
data_cov = np.cov(data, rowvar=False)

# انجام تجزیه ویژه
eigenvalues, eigenvectors = np.linalg.eigh(data_cov)

# مقیاس‌دهی مؤلفه‌های اصلی برای مصورسازی
scaling_factor = 2  # فاکتور مقیاس دلخواه برای مصورسازی بهتر
pc1 = eigenvectors[:, 1] * eigenvalues[1] * scaling_factor  # اولین مؤلفه اصلی (بزرگترین مقدار ویژه)
pc2 = eigenvectors[:, 0] * eigenvalues[0] * scaling_factor  # دومین مؤلفه اصلی (کوچکترین مقدار ویژه)

# رسم داده‌ها
plt.figure(figsize=(6, 6))
plt.scatter(data[:, 0], data[:, 1], alpha=0.5, s=10, label="داده")
plt.axhline(0, color="gray", linestyle="--", linewidth=0.8)
plt.axvline(0, color="gray", linestyle="--", linewidth=0.8)

# افزودن محورهای اصلی اول و دوم
plt.quiver(mean[0], mean[1], pc1[0], pc1[1], angles="xy", scale_units="xy", scale=1, color="red", label="اولین مؤلفه اصلی")
plt.quiver(mean[0], mean[1], pc2[0], pc2[1], angles="xy", scale_units="xy", scale=1, color="blue", label="دومین مؤلفه اصلی")

# افزودن برچسب‌ها و عنوان
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("نمودار پراکنده با مؤلفه‌های اصلی اول و دوم")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.legend()
plt.grid(True)
plt.show()

جهت تصادفی در مقابل مؤلفه اصلی: اینجا یک راستای دیگر از داده ها را برای پروجکشن نشان می دهد که مطابق خرجی روش مولفه اصلی PCA نیست

تعریف

هدف: کاهش ابعاد داده‌ها در حین حفظ جنبه‌های مهم داده.

فرض کنید $ \mathbf{X} $:

\[\mathbf{X} = \begin{pmatrix} \mathbf{X}_1^\top \\ \vdots \\ \mathbf{X}_N^\top \end{pmatrix}_{N \times d} = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} \\ x_{21} & x_{22} & \cdots & x_{2d} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N1} & x_{N2} & \cdots & x_{Nd} \end{pmatrix}\] \[\mathbf{X}_{N \times d} \xrightarrow{\text{PCA}} \tilde{\mathbf{X}}_{N \times k} \quad \text{با} \quad k \leq d\]

فرض: داده‌ها میانگین-مرکزی شده‌اند، یعنی:
\[\mu_x = \frac{1}{N} \sum_{i=1}^N \mathbf{X}_i = \mathbf{0}_{d \times 1}\]

تفسیرها

تصویر متعامد داده‌ها بر روی یک زیرفضای خطی با ابعاد پایین‌تر که: تفسیر ۱. واریانس داده‌های تصویر شده را بیشینه می‌کند. تفسیر ۲. مجموع مربعات فواصل تا زیرفضا را کمینه می‌کند.

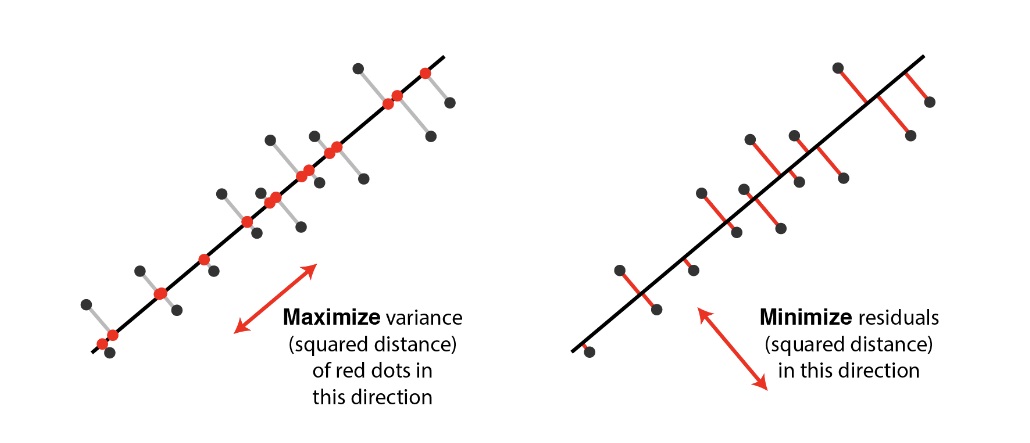
کمینه کردن مجموع مربعات فواصل تا زیرفضا معادل است با بیشینه کردن مجموع مربعات تصاویر بر روی آن زیرفضا

یک مجموعه از بردارهای متعامد واحد $\mathbf{v} = \mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_k$ (که هر $ \mathbf{v}_i $ به اندازه $ d \times 1 $ است) که توسط PCA تولید می‌شوند و هر دو تفسیر را انجام می‌دهند.

بیشینه کردن واریانس داده‌های تصویر شده

تصویر نقاط داده بر روی $\mathbf{v}_1$:

\[\Pi = \Pi_{\mathbf{v}_1}\{ \mathbf{X}_1, \dots, \mathbf{X}_N \} = \{ \mathbf{v}_1^\top \mathbf{X}_1, \dots, \mathbf{v}_1^\top \mathbf{X}_N \}\]

توجه کنید که: $Var(\mathbf{X}) = \mathbb{E}[\mathbf{X}^2] - \mathbb{E}[\mathbf{X}]^2$

\[\mathbb{E}[\mathbf{X}] = 0 \implies Var(\Pi) = \frac{1}{N} \sum_{i=1}^N (\mathbf{v}_1^\top \mathbf{X}_i)^2\]

مرکزی کردن میانگین داده
- صفر کردن میانگین هر ویژگی
مقیاس‌دهی برای نرمال کردن هر ویژگی به داشتن واریانس ۱ (یک مرحله دلخواه)
- ممکن است بر نتایج تأثیر بگذارد
- زمانی کمک می‌کند که واحدهای اندازه‌گیری ویژگی‌ها متفاوت باشند و برخی ویژگی‌ها بدون نرمال سازی نادیده گرفته شوند.

پیش‌زمینه

قبل از شروع الگوریتم PCA، باید با موارد زیر آشنا باشیم:

مقادیر ویژه و بردارهای ویژه چیستند؟
ماتریس کوواریانس نمونه

مقادیر ویژه و بردارهای ویژه چیستند؟

بردار ویژه: یک بردار غیرصفر که وقتی یک تبدیل خطی اعمال می‌شود فقط در یک ضریب اسکالر ضرب می‌شود. مقدار ویژه: ضریب اسکالری که بردار ویژه در آن مقیاس می‌شود. معادله برای یک ماتریس n×n:

\[Av = \lambda v\]

جایی که:

A: یک ماتریس مربعی

v: بردار ویژه

$ \lambda $: مقدار ویژه

تفسیر هندسی

بردارهای ویژه پس از تبدیل در همان جهت (یا مخالف) اشاره می‌کنند. بردارهای ویژه تحت یک تبدیل جهت خود را تغییر نمی‌دهند. مقادیر ویژه نشان می‌دهند که بردار چقدر کشیده یا فشرده شده است. مقادیر ویژه به ما می‌گویند که بردار چقدر مقیاس شده است.

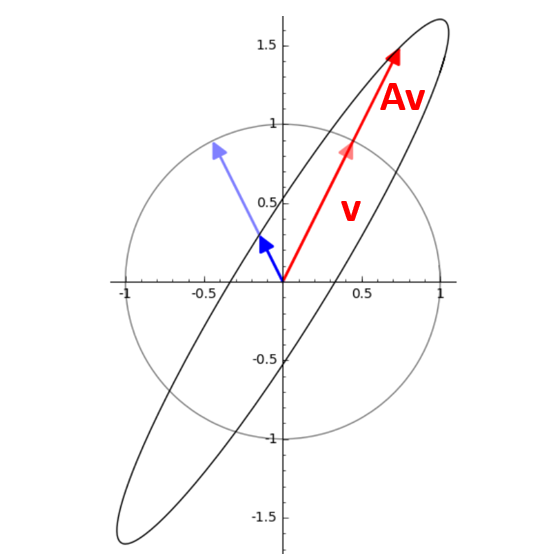
چگونه مقادیر ویژه و بردارهای ویژه را پیدا کنیم؟

می‌دانیم که

\[Av = \lambda v\]

پس

\[Av - \lambda v=0\] \[(Av - \lambda I) v=0\]

v نمی‌تواند صفر باشد، بنابراین:

\[det(Av - \lambda I)=0\]

برای $\lambda $ حل کنید. $ \lambda $ را دوباره در معادله $ Av=\lambda v $ جایگزین کنید تا v را پیدا کنید.

مثال عددی

فرض کنید

\[A = \begin{pmatrix} 4 & -5 \\ 2 & -3 \end{pmatrix}\]

آنگاه

\[A-\lambda I= \begin{pmatrix} 4-\lambda & -5 \\ 2 & -3-\lambda \end{pmatrix}\] \[دترمینان (A- \lambda I)= (4-\lambda)(-3-\lambda)+10=(\lambda)^2-\lambda-2=0\] \[\lambda=-1 یا \lambda=2\] \[for \lambda_1=-1: (A- \lambda_1 I)v_1= \begin{pmatrix} 5 & -5 \\ 2 & -2 \end{pmatrix} \begin{pmatrix} v_{11} \\ v_{12} \end{pmatrix} = \begin{pmatrix} 0 \\0 \end{pmatrix} \implies v_1=\begin{pmatrix} 1 \\1 \end{pmatrix}\] \[for \lambda_2=2: (A- \lambda_2 I)v_2= \begin{pmatrix} 2 & -5 \\ 2 & -5 \end{pmatrix} \begin{pmatrix} v_{21} \\ v_{22} \end{pmatrix} = \begin{pmatrix} 0 \\0 \end{pmatrix} \implies v_2=\begin{pmatrix} 5 \\2 \end{pmatrix}\]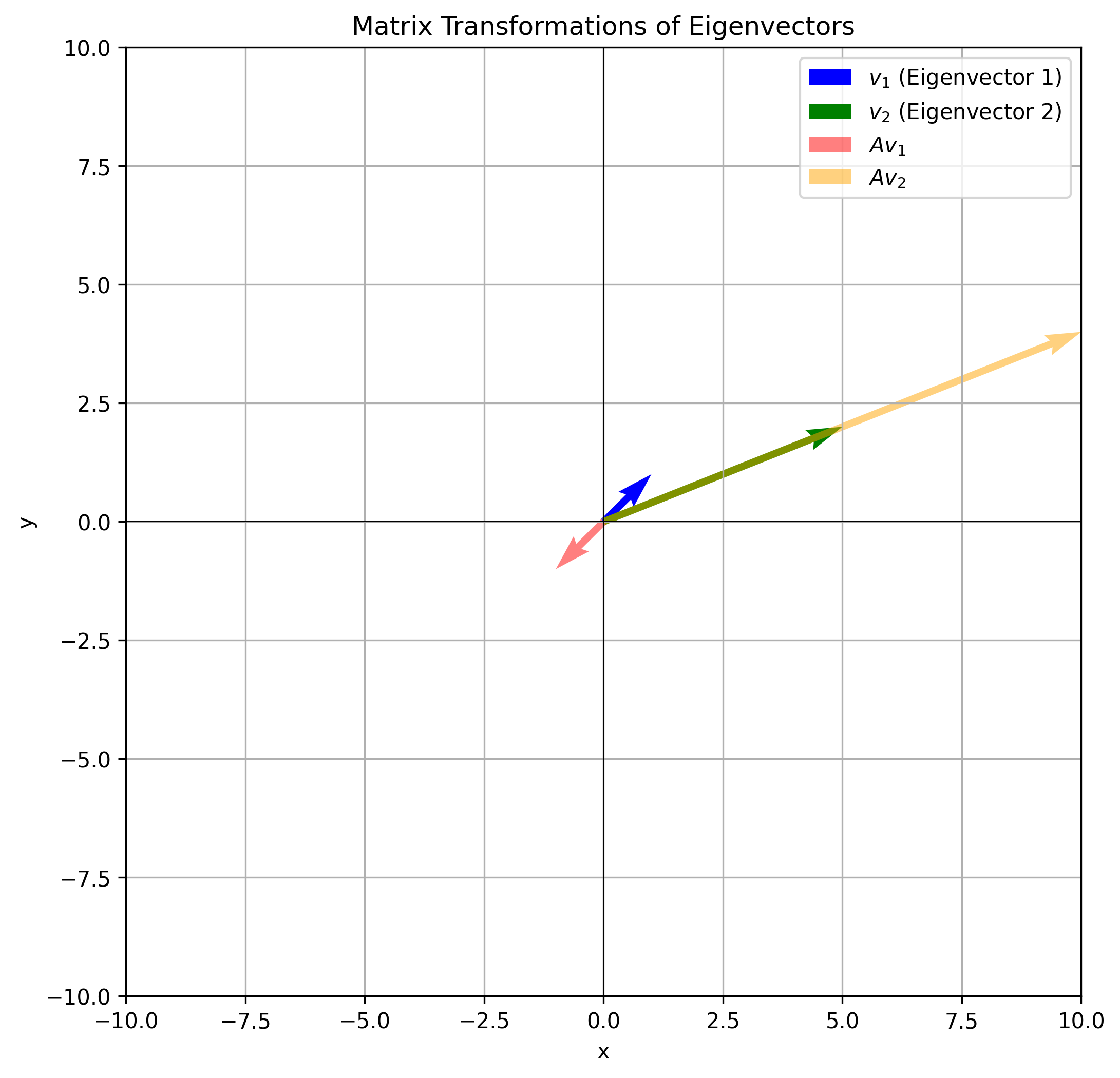

کوواریانس چیست؟

کوواریانس معیاری است از این که دو ویژگی تصادفی چقدر با هم تغییر می‌کنند.

\[Cov(X,Y) = E[(X −E[X])(Y −E[Y])] = E[(Y −E[Y])(X −E[X])] = Cov(Y,X)\]

بنابراین کوواریانس متقارن است. مانند قد و وزن افراد.

#### ماتریس کوواریانس چیست؟ یک ماتریس کوواریانس مفهوم کوواریانس را به چندین ویژگی تعمیم می‌دهد. فرض کنید ماتریس کوواریانس دو ویژگی وجود دارد:

\[\Sigma = \begin{pmatrix} a & b \\ c & d \end{pmatrix} =\begin{pmatrix} a & b \\ b & d \end{pmatrix}\]

چرا b=c؟

رابطه بین a,b و d چیست؟

مثال ماتریس کوواریانس

$\Sigma = \begin{pmatrix} a & 0 \\ 0 & a \end{pmatrix}$

کد: مثال

این کد پایتون داده‌های 2 بعدی را از یک توزیع نرمال چندمتغیره با میانگین [0, 0] و ماتریس کوواریانس زیر تولید و مصورسازی می‌کند:

\[\Sigma = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\]

ماتریس کوواریانس نشان‌دهنده متغیرهای مستقل با هیچ همبستگی است. کد یک نمودار پراکندگی از 1000 نمونه ایجاد می‌کند، با مقیاس‌دهی برابر برای هر دو محور و خطوط شبکه برای نمایش بهتر توزیع داده‌ها، که باید به دلیل عدم همبستگی بین متغیرها دایره‌ای ظاهر شود.

import numpy as np
import matplotlib.pyplot as plt

# تعریف بردار میانگین و ماتریس کوواریانس
mean = [0, 0]  # مثال: داده 2 بعدی با میانگین صفر
cov = [[1, 0], 
       [0, 1]]  # ماتریس کوواریانس (2x2)

# تعداد نمونه‌ها
n_samples = 1000

# تولید داده
data = np.random.multivariate_normal(mean, cov, size=n_samples)

plt.scatter(data[:,0], data[:,1])
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("داده‌های پراکنده")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.grid(True)
plt.show()

\[\Sigma = \begin{pmatrix} a & 0 \\ 0 & d \end{pmatrix}\]

کد: مثال

\[\Sigma = \begin{bmatrix} 4 & 0 \\ 0 & 1 \end{bmatrix}\]

ماتریس کوواریانس نشان می‌دهد که متغیرها واریانس‌های متفاوتی (4 و 1) دارند اما هیچ همبستگی ندارند. نمودار پراکندگی 1000 نمونه یک توزیع بیضوی را نشان خواهد داد، با گسترش بیشتر در امتداد محور X به دلیل واریانس بزرگتر 4 در آن جهت. نمودار شامل نسبت ابعاد برابر و خطوط شبکه برای مصورسازی بهتر است.

import numpy as np
import matplotlib.pyplot as plt

# تعریف بردار میانگین و ماتریس کوواریانس
mean = [0, 0]  # مثال: داده 2 بعدی با میانگین صفر
cov = [[4, 0], 
       [0, 1]]  # ماتریس کوواریانس (2x2)

# تعداد نمونه‌ها
n_samples = 1000

# تولید داده
data = np.random.multivariate_normal(mean, cov, size=n_samples)

plt.scatter(data[:,0], data[:,1])
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("داده‌های پراکنده")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.grid(True)
plt.show()

\[\Sigma = \begin{pmatrix} a & b \\ b & d \end{pmatrix}\]

a>d و b>0

کد: مثال

این کد پایتون داده‌های 2 بعدی را از یک توزیع نرمال چندمتغیره با میانگین [0, 0] و ماتریس کوواریانس زیر تولید و مصورسازی می‌کند: $\Sigma = \begin{bmatrix} 10 & 4 \\ 4 & 2 \end{bmatrix}$

ماتریس کوواریانس نشان می‌دهد که متغیرها واریانس‌های متفاوتی (10 و 2) و یک همبستگی مثبت 4 دارند. نمودار پراکندگی 1000 نمونه یک توزیع بیضوی را نشان خواهد داد، با نقاط داده که به دلیل واریانس بزرگتر (10) بیشتر در امتداد محور X پخش شده‌اند و یک شکل کج به دلیل همبستگی مثبت بین متغیرها. نمودار شامل نسبت ابعاد برابر و خطوط شبکه برای مصورسازی بهتر است.

import numpy as np
import matplotlib.pyplot as plt

# تعریف بردار میانگین و ماتریس کوواریانس
mean = [0, 0]  # مثال: داده 2 بعدی با میانگین صفر
cov = [[10, 4], 
       [4, 2]]  # ماتریس کوواریانس (2x2)

# تعداد نمونه‌ها
n_samples = 1000

# تولید داده
data = np.random.multivariate_normal(mean, cov, size=n_samples)

plt.scatter(data[:,0], data[:,1])
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("داده‌های پراکنده")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.grid(True)
plt.show()

\[\Sigma = \begin{pmatrix} a & b \\ b & d \end{pmatrix}\]

a>d و b<0

کد: مثال

\[\Sigma = \begin{bmatrix} 10 & -4 \\ -4 & 2 \end{bmatrix}\]

ماتریس کوواریانس نشان می‌دهد که متغیرها واریانس‌های متفاوتی (10 و 2) و یک همبستگی منفی 4- دارند. نمودار پراکندگی 1000 نمونه یک توزیع بیضوی را نشان خواهد داد، با نقاط داده که به دلیل واریانس بزرگتر (10) بیشتر در امتداد محور X پخش شده‌اند و یک شکل کج به دلیل همبستگی منفی بین متغیرها. نمودار شامل نسبت ابعاد برابر و خطوط شبکه برای مصورسازی بهتر است.

import numpy as np
import matplotlib.pyplot as plt

# تعریف بردار میانگین و ماتریس کوواریانس
mean = [0, 0]  # مثال: داده 2 بعدی با میانگین صفر
cov = [[10, -4], 
       [-4, 2]]  # ماتریس کوواریانس (2x2)

# تعداد نمونه‌ها
n_samples = 1000

# تولید داده
data = np.random.multivariate_normal(mean, cov, size=n_samples)

plt.scatter(data[:,0], data[:,1])
plt.xlabel("محور X")
plt.ylabel("محور Y")
plt.title("داده‌های پراکنده")
plt.gca().set_aspect("equal")  # نسبت ابعاد برابر
plt.grid(True)
plt.show()

بیان واریانس

واریانس داده‌های تصویر شده بر روی جهت $v$ است: $\text{VAR}(X\mathbf{v}) = \frac{1}{n} \sum_{i=1}^n (x_i^T\mathbf{v})^2$
این را می‌توان به صورت زیر نوشت: $\text{VAR}(X\mathbf{v}) = \frac{1}{n} ||X\mathbf{v}||^2 = \frac{1}{n} \mathbf{v}^TX^TX\mathbf{v} = \mathbf{v}^T \Sigma \mathbf{v}$

مسئله بیشینه‌سازی

ما هدفمان بیشینه کردن واریانس $\mathbf{v}^T\Sigma \mathbf{v}$ تحت قید $

\mathbf{v}

=1 $ است.

این منجر به مسئله بهینه‌سازی زیر می‌شود: $\max_{v} \mathbf{v}^T \Sigma \mathbf{v} \text{ به شرط } ||\mathbf{v}||=1$

استفاده از ضرب‌کننده‌های لاگرانژ

یک ضرب‌کننده لاگرانژ $\lambda$ معرفی می‌کنیم و لاگرانژی را تعریف می‌کنیم: $L(\mathbf{v},\lambda)=\mathbf{v}^T \Sigma \mathbf{v} - \lambda (\mathbf{v}^T\mathbf{v} - 1)$
گرفتن مشتق نسبت به $\mathbf{v}$ و تنظیم آن بر 0: $\frac{\partial{L}}{\partial{\mathbf{v}}} = 2\Sigma \mathbf{v} - 2 \lambda \mathbf{v} = 0$
این به سادگی می‌شود: $\Sigma \mathbf{v} = \lambda \mathbf{v}$
ما همه $(\mathbf{v}_1, \lambda_1), (\mathbf{v}_2, \lambda_2), ... ,(\mathbf{v}_k, \lambda_k)$ را به عنوان $k$ بردار ویژه $\Sigma$ با بزرگترین مقادیر ویژه تعریف می‌کنیم: $\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_k$

تفسیر

واریانس $\mathbf{v}^T \Sigma \mathbf{v}$ وقتی بیشینه می‌شود که $\mathbf{v}$ بردار ویژه متناظر با بزرگترین مقدار ویژه $\Sigma$ باشد.
مقدار ویژه $\lambda$ نشان‌دهنده واریانس در جهت بردار ویژه $\mathbf{v}$ است.
نتیجه: بردارهای ویژه ماتریس کوواریانس واریانس داده‌های تصویر شده را بیشینه می‌کنند.

کد:

این کد پایتون تحلیل مؤلفه‌های اصلی (PCA) را روی مجموعه داده شبیه MNIST از sklearn.datasets انجام می‌دهد. مجموعه داده ابتدا بارگیری و تغییر شکل داده می‌شود، با مقادیر پیکسل نرمال شده. تابع pca مؤلفه‌های اصلی را با مرکزی کردن داده (کم کردن میانگین)، محاسبه ماتریس کوواریانس و به دست آوردن بردارهای ویژه و مقادیر ویژه آن محاسبه می‌کند. بردارهای ویژه برتر برای تصویر داده در یک فضای کاهش یافته انتخاب می‌شوند. کد مجموعه داده را به 20 مؤلفه اصلی کاهش می‌دهد و دو مؤلفه اصلی اول را در یک نمودار پراکندگی، رنگ‌آمیزی شده با برچسب‌های رقم، مصورسازی می‌کند. این مصورسازی به مشاهده چگونگی توزیع داده در فضای کاهش-بعدی کمک می‌کند.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

data = load_digits()
mnist = data.images
labels = data.target

mnist = mnist.reshape(-1, 64)

mnist = mnist.astype('float32') / 255.0
labels = labels.astype(int)
num_pcs = 20

def pca(X, num_components):
    X_meaned = X - np.mean(X, axis=0)
    covariance_matrix = np.cov(X_meaned, rowvar=False)
    print(X.shape)
    print(covariance_matrix.shape)
    eigenvalues, eigenvectors = np.linalg.eigh(covariance_matrix)
    sorted_index = np.argsort(eigenvalues)[::-1]
    sorted_eigenvectors = eigenvectors[:, sorted_index]
    eigenvector_subset = sorted_eigenvectors[:, :num_components]
    X_reduced = np.dot(X_meaned, eigenvector_subset)
    return X_reduced, eigenvector_subset

mnist_reduced, eigenvector_subset = pca(mnist, num_pcs)
print(mnist_reduced.shape)
plt.figure(figsize=(8, 6))
scatter = plt.scatter(mnist_reduced[:, 0], mnist_reduced[:, 1], c=labels, cmap='tab10', alpha=0.7)
plt.colorbar(scatter)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

کد:

این کد پایتون مجموعه داده MNIST کاهش یافته را با استفاده از معکوس تبدیل PCA تجزیه می‌کند. mnist_decompressed با ضرب داده کاهش یافته (mnist_reduced) در ترانهاده بردارهای ویژه (eigenvector_subset.T) و اضافه کردن میانگین مجموعه داده اصلی بازسازی می‌شود. تابع visualize_decompression تصاویر اصلی و تجزیه شده را برای مقایسه کنار هم نمایش می‌دهد. این تابع هر دو داده اصلی و تجزیه شده را به فرمت تصویر تغییر شکل می‌دهد و 5 تصویر اول را به همراه نسخه‌های تجزیه شده آن‌ها نشان می‌دهد، که یک نمایش بصری از چگونگی حفظ جزئیات تصویر توسط فرآیند فشرده‌سازی و تجزیه PCA ارائه می‌دهد.

mnist_decompressed = np.dot(mnist_reduced, eigenvector_subset.T) + np.mean(mnist, axis=0)

def visualize_decompression(original, decompressed, img_shape, num_images=5, title=""):
    original = original.reshape(-1, *img_shape)
    decompressed = decompressed.reshape(-1, *img_shape)

    plt.figure(figsize=(10, 4))

    for i in range(num_images):
        plt.subplot(2, num_images, i + 1)
        plt.imshow(original[i])
        plt.axis('off')

        plt.subplot(2, num_images, num_images + i + 1)
        plt.imshow(decompressed[i])
        plt.axis('off')

    plt.tight_layout()
    plt.show()


visualize_decompression(mnist[:5], mnist_decompressed[:5], img_shape=(8, 8), title="MNIST")

درک چرخش داده در تحلیل مؤلفه‌های اصلی (PCA)

در تحلیل مؤلفه‌های اصلی (PCA)، هدف اولیه کاهش ابعاد داده در حین حفظ تا حد امکان واریانس است. یک مؤلفه کلیدی این فرآیند شامل چرخش داده برای تراز با محورهای جدیدی است که جهات بیشینه واریانس را ثبت می‌کنند. این چرخش از نظر ریاضی با تبدیل داده اصلی با استفاده از بردارهای ویژه ماتریس کوواریانس به دست می‌آید و نقش مرکزی در فرآیند کاهش ابعاد ایفا می‌کند.

1. ماتریس کوواریانس و بردارهای ویژه

در PCA، اولین قدم محاسبه ماتریس کوواریانس مجموعه داده است که روابط و وابستگی‌های بین ویژگی‌های مختلف را نشان می‌دهد. ماتریس کوواریانس به صورت زیر تعریف می‌شود:

\[\text{Cov}(X) = \frac{1}{N-1} X^T X\]

جایی که $(X)$ ماتریس داده به اندازه $(n \times d)$ است (با $(n)$ تعداد نمونه‌ها و $(d)$ تعداد ویژگی‌ها)، و $(N)$ تعداد نمونه‌ها است.

از ماتریس کوواریانس، سپس مقادیر ویژه و بردارهای ویژه را محاسبه می‌کنیم. بردارهای ویژه نشان‌دهنده جهات محورهای جدید (مؤلفه‌های اصلی) هستند و مقادیر ویژه نشان‌دهنده مقدار واریانس ثبت شده توسط هر مؤلفه اصلی هستند.

\[\text{Cov}(X) = V \Lambda V^T\]

جایی که:

$(V)$ ماتریس بردارهای ویژه است،
$(\Lambda)$ ماتریس قطری مقادیر ویژه است.

2. تبدیل داده (چرخش)

هنگامی که بردارهای ویژه را داریم، می‌توانیم داده را با تصویر کردن آن بر روی پایه جدید تعریف شده توسط بردارهای ویژه بچرخانیم. این تبدیل به صورت زیر نشان داده می‌شود:

\[X_{n \times d} V_{d \times d} = \hat{X}_{n \times d}\]

در اینجا، $(X)$ ماتریس داده اصلی است، $(V)$ ماتریس بردارهای ویژه است و $(\hat{X})$ داده تبدیل شده (یعنی داده پس از چرخش) است.

نقاط داده اکنون در امتداد مؤلفه‌های اصلی تراز شده‌اند، جایی که اولین مؤلفه اصلی بیشترین واریانس را ثبت می‌کند و مؤلفه‌های بعدی مقادیر کاهش یافته واریانس را ثبت می‌کنند. این چرخش امکان نمایش معنادارتر داده را فراهم می‌کند، به ویژه هنگام کاهش ابعاد.

3. ماتریس کوواریانس در فضای تبدیل شده

پس از چرخش داده، می‌توانیم ماتریس کوواریانس داده تبدیل شده، $(\hat{X})$ را محاسبه کنیم که در حالت ایده‌آل باید قطری باشد. تبدیل اطمینان حاصل می‌کند که کوواریانس بین مؤلفه‌های مختلف در فضای جدید صفر است، که یک ویژگی کلیدی PCA است. ماتریس کوواریانس داده تبدیل شده را می‌توان به صورت زیر بیان کرد:

\[\text{Cov}(\hat{X}) = V^T \text{Cov}(X) V = \Lambda\]

از آنجایی که بردارهای ویژه متعامد هستند، ماتریس کوواریانس در فضای جدید قطری است، با مقادیر ویژه روی قطر. این قطری شدن نشان می‌دهد که مؤلفه‌های اصلی جدید ناهمبسته هستند.

4. مشتق دقیق کوواریانس در فضای تبدیل شده

با شروع با ماتریس کوواریانس داده اصلی، تبدیل را با بردارهای ویژه اعمال می‌کنیم:

\[\text{Cov}(X V) = \frac{1}{N-1} (X V)^T (X V)\]

این را می‌توان به صورت زیر گسترش داد:

\[= \frac{1}{N-1} V^T X^T X V\]

بعد، ماتریس کوواریانس اصلی را جایگزین می‌کنیم:

\[= \frac{1}{N-1} V^T \text{Cov}(X) V\]

با استفاده از این واقعیت که ماتریس کوواریانس $(

با شروع از ماتریس کوواریانس داده‌های اصلی، تبدیل را با بردارهای ویژه اعمال می‌کنیم:

\[\text{Cov}(X V) = \frac{1}{N-1} (X V)^T (X V)\]

این عبارت را می‌توان به صورت زیر بسط داد:

\[= \frac{1}{N-1} V^T X^T X V\]

در مرحله بعد، ماتریس کوواریانس اصلی را جایگزین می‌کنیم:

\[= \frac{1}{N-1} V^T \text{Cov}(X) V\]

با استفاده از این واقعیت که ماتریس کوواریانس $(X)$ توسط بردارهای ویژه قطری می‌شود:

\[\text{Cov}(X) = V \Lambda V^T\]

به دست می‌آوریم:

\[\text{Cov}(X V) = \frac{1}{N-1} V^T (V \Lambda V^T) V\]

از آنجا که بردارهای ویژه متعامد هستند، داریم $(V^T V = I)$، بنابراین:

\[= \frac{1}{N-1} (V^T V) \Lambda (V^T V) = \frac{1}{N-1} \Lambda\]

این نشان می‌دهد که ماتریس کوواریانس داده‌های تبدیل‌شده $(\hat{X})$ یک ماتریس قطری است که مقادیر ویژه $(\Lambda)$ روی قطر اصلی آن قرار دارند.

۵. تفسیر هندسی

از دیدگاه هندسی، این فرآیند مشابه یک چرخش داده در فضای ویژگی است. بردارهای ویژه، محورهای جدید داده را تعیین می‌کنند و مقادیر ویژه نشان می‌دهند که چه مقدار واریانس در امتداد هر یک از این محورهای جدید وجود دارد. با تبدیل داده‌ها به این فضای جدید، ما به طور مؤثر سیستم مختصات را به گونه‌ای تغییر جهت می‌دهیم که جهت‌های حداکثر واریانس (مؤلفه‌های اصلی) با محورها تراز شوند.

در عمل، هنگام کاهش ابعاد داده‌ها (مثلاً با حفظ تنها چند مؤلفه اصلی برتر)، بر مهم‌ترین جهت‌های واریانس تمرکز کرده و جهت‌های کم‌اهمیت‌تر را کنار می‌گذاریم. این به ساده‌سازی داده‌ها کمک می‌کند در حالی که مهم‌ترین ویژگی‌ها حفظ می‌شوند.

استفاده از بردارهای ویژه و مقادیر ویژه در PCA، چرخش داده‌ها را به یک سیستم مختصات جدید ممکن می‌سازد که در آن محورها با جهت‌های حداکثر واریانس مطابقت دارند. این تبدیل به درک بهتر ساختار داده کمک می‌کند و گامی اساسی در کاهش ابعاد، استخراج ویژگی و کاهش نویز است. با تمرکز بر مهم‌ترین مؤلفه‌ها، می‌توانیم به نمایشی کارآمدتر از داده دست یابیم.

این فرآیند کامل چرخش داده در PCA، ساده‌سازی مجموعه داده‌های پیچیده را ممکن می‌سازد و تجسم و تحلیل الگوهای زیربنایی در داده را آسان‌تر می‌کند.

import numpy as np
import matplotlib.pyplot as plt

# 1. Generate melon-shaped data
def generate_data(n_samples=100):
    np.random.seed(42)  # For reproducibility
    x = np.random.normal(0, 1, n_samples)
    y = 0.5 * x + np.random.normal(0, 0.1, n_samples)  # Elongated data
    return np.column_stack((x, y))

# Generate data matrix
data = generate_data()

# 2. Compute the covariance matrix of the original data
cov_matrix_data = np.cov(data, rowvar=False)

# 3. Compute eigenvalues and eigenvectors
eig_values, eig_vectors = np.linalg.eig(cov_matrix_data)

# 4. Transform the data using eigenvectors
x_hat = data @ eig_vectors

# 5. Compute the covariance matrix of the transformed data
cov_matrix_x_hat = np.cov(x_hat, rowvar=False)

# 6. Plot data and covariance matrices
fig, axes = plt.subplots(2, 2, figsize=(12, 12))

# Plot original data
axes[0, 0].scatter(data[:, 0], data[:, 1], alpha=0.7, edgecolor='k')
axes[0, 0].set_title('Original Data')
axes[0, 0].axis('equal')

# Plot eigenvectors on original data
for i in range(len(eig_values)):
    vector = eig_vectors[:, i] * np.sqrt(eig_values[i]) * 2
    axes[0, 0].quiver(0, 0, vector[0], vector[1], angles='xy', scale_units='xy', scale=1, color='r', alpha=0.8)

# Plot transformed data
axes[0, 1].scatter(x_hat[:, 0], x_hat[:, 1], alpha=0.7, edgecolor='k')
axes[0, 1].set_title('Transformed Data')
axes[0, 1].axis('equal')

# Plot covariance matrix of original data
im1 = axes[1, 0].imshow(cov_matrix_data, cmap='viridis', interpolation='none')
axes[1, 0].set_title('Covariance Matrix of Original Data')
plt.colorbar(im1, ax=axes[1, 0])

# Plot covariance matrix of transformed data
im2 = axes[1, 1].imshow(cov_matrix_x_hat, cmap='viridis', interpolation='none')
axes[1, 1].set_title('Covariance Matrix of Transformed Data')
plt.colorbar(im2, ax=axes[1, 1])

plt.tight_layout()
plt.show()

کد:

این پروژه از PCA برای تحلیل مجموعه‌داده‌ای ساخته‌شده از تصاویر خاکستری تمام دانش‌ جویان یک کلاس استفاده می‌کند. مجموعه‌داده که در lfw_people ذخیره شده، با بارگذاری تصاویر از یک دایرکتوری ساخته می‌شود. علاوه بر این، یک تصویر تست جداگانه برای ارزیابی بارگذاری می‌شود.

هدف کاهش ابعاد تصاویر با استفاده از PCA در حالی است که مهم‌ترین ویژگی‌ها حفظ شوند. تابع pca، ۱۰ مؤلفه اصلی برتر را استخراج می‌کند. اولین مؤلفه اصلی که به صورت یک تصویر可视化 می‌شود، نمایان‌گر dominantترین ویژگی مشترک در میان عکس‌های کلاس است.

سپس اسکریپت، هر دو مجموعه‌داده کلاس و تصویر تست را فشرده و بازسازی می‌کند. تابع visualize_decompression تصاویر اصلی و بازسازی‌شده را کنار هم نمایش می‌دهد و برجسته می‌کند که PCA چقدر خوب اطلاعات حیاتی را حفظ می‌کند.

این تحلیل نشان می‌دهد که PCA چگونه می‌تواند داده‌های تصویری را ساده کند، و بازسازی و فشرده‌سازی عکس‌های کلاس را به طور مؤثر نمایش می‌دهد در حالی که شباهت بصری را حفظ می‌کند.

from sklearn.datasets import fetch_olivetti_faces
from matplotlib import pyplot as plt
import numpy as np
import cv2
import os

src = './data/'
files = os.listdir(src)
lfw_people = []
for file in files:
    lfw_people.append(cv2.imread(src+file, 0))
lfw_people = np.array(lfw_people)

name = ['resized_parvaz.png','resized_mahdieh.jpg']
test = cv2.imread('./img/'+name[0], 0).reshape(1, 64, 64)

print(test.shape)
print(lfw_people.shape)

num_pcs = 10
def pca(X, num_components):
    mean_face = np.mean(X, axis=0)
    X_meaned = X - np.mean(X, axis=0)
    covariance_matrix = np.cov(X_meaned, rowvar=False)
    print(X.shape)
    print(covariance_matrix.shape)
    eigenvalues, eigenvectors = np.linalg.eigh(covariance_matrix)
    sorted_index = np.argsort(eigenvalues)[::-1]
    sorted_eigenvectors = eigenvectors[:, sorted_index]
    eigenvector_subset = sorted_eigenvectors[:, :num_components]
    X_reduced = np.dot(X_meaned, eigenvector_subset)
    return X_reduced, eigenvector_subset, mean_face

# آموزش
mnist_reduced, eigenvector_subset, mean_face = pca(lfw_people.reshape(-1, 64*64), num_pcs)

plt.figure(figsize=(12, 8))
grid_cols = 5  # تنظیم ستون‌های grid
grid_rows = (num_pcs + 1) // grid_cols + 1  # تنظیم پویای سطرهای grid

plt.subplot(grid_rows, grid_cols, 1)
plt.title("میانگین چهره")
plt.imshow(mean_face.reshape(64,64), cmap="gray")
plt.axis("off")

# نمایش چهره‌های ویژه
for i in range(num_pcs):
    plt.subplot(grid_rows, grid_cols, i + 2)
    plt.title(f"چهره ویژه {i + 1}")
    plt.imshow(eigenvector_subset[:, i].reshape(64,64), cmap="gray")
    plt.axis("off")

plt.tight_layout()
plt.show()


# تست
test_reduced = np.dot(test.reshape(-1, 64*64), eigenvector_subset)
print(eigenvector_subset.shape)

mnist_decompressed = np.dot(mnist_reduced, eigenvector_subset.T) + np.mean(lfw_people.reshape(-1, 64*64), axis=0)
test_decompressed = np.dot(test_reduced, eigenvector_subset.T)

def visualize_decompression(original, decompressed, img_shape, num_images=13, title=""):
    original = original.reshape(-1, *img_shape)
    decompressed = decompressed.reshape(-1, *img_shape)

    plt.figure(figsize=(10, 4))

    for i in range(num_images):
        plt.subplot(2, num_images, i + 1)
        plt.imshow(original[i])
        plt.axis('off')

        plt.subplot(2, num_images, num_images + i + 1)
        plt.imshow(decompressed[i])
        plt.axis('off')

    plt.tight_layout()
    plt.show()


visualize_decompression(lfw_people, mnist_decompressed, (64, 64), title="بازسازی PCA")
visualize_decompression(test, test_decompressed, (64, 64), num_images=1, title="بازسازی PCA")

اگر به جای مقادیر ویژه بزرگ از مقادیر ویژه کوچک در پروژه چهره‌های ویژه استفاده کنیم چه اتفاقی می‌افتد؟

در زمینه پروژه چهره‌های ویژه، که در آن از تحلیل مؤلفه‌های اصلی (PCA) برای شناسایی مؤلفه‌های اصلی (چهره‌های ویژه) تصاویر چهره استفاده می‌شود، مقادیر ویژه نمایان‌گر واریانس captured شده توسط هر مؤلفه اصلی هستند. مقادیر ویژه بزرگ با مهم‌ترین ویژگی‌های داده مطابقت دارند، مانند ویژگی‌های اصلی یک چهره (مثلاً شکل کلی، چشم‌ها، بینی)، در حالی که مقادیر ویژه کوچک با تغییرات ریزتر و جزئی‌تر مطابقت دارند که اغلب ویژگی‌های کم‌اهمیت‌تر را capture می‌کنند.

اگر به جای مقادیر بزرگ از مقادیر کوچک استفاده کنیم، در واقع بر ویژگی‌هایی با واریانس پایین تأکید کرده‌ایم. این ویژگی‌ها معمولاً کم‌برجسته‌تر هستند و اغلب مربوط به جزئیات ظریف یا نویز در داده‌ها هستند، نه ویژگی‌های غالب چهره. در نتیجه، چهره‌های بازسازی‌شده با استفاده از مقادیر ویژه کوچک ممکن است distorted، کمتر قابل تشخیص یا تار به نظر برسند زیرا بر تغییرات جزئی و کم‌اهمیت‌تر در تصاویر تمرکز می‌کنند.

استفاده از مقادیر ویژه کوچک ممکن است نویز پس‌زمینه، تغییرات جزئی نورپردازی یا نواقص کوچک در تصاویر را نیز برجسته کند که بخشی از ساختار اصلی چهره نیستند. در حالی که این ممکن است برخی جزئیات خاص را capture کند، به نمایش دقیق ویژگی‌های کلیدی چهره که توسط مقادیر ویژه بزرگتر نمایش داده می‌شوند کمک نمی‌کند.

به طور خلاصه، استفاده از مقادیر ویژه کوچک در پروژه چهره‌های ویژه می‌تواند منجر به overfitting شود با تمرکز بر ویژگی‌های نامربوط و نویز، در حالی که ویژگی‌های مهم‌تر و غالب که برای تشخیص دقیق چهره‌ها حیاتی هستند نادیده گرفته می‌شوند. بنابراین، معمولاً استفاده از مقادیر ویژه بزرگ ترجیح داده می‌شود تا اطمینان حاصل شود که مهم‌ترین و generalizableترین ویژگی‌های چهره به طور مؤثر capture و نمایش داده می‌شوند.

کد مربوط به آزمایش با مقادیر ویژه کوچک

(این بخش از کد مشابه کد قبلی است اما با مرتب‌سازی معکوس برای انتخاب مقادیر کوچک)

from sklearn.datasets import fetch_olivetti_faces
from matplotlib import pyplot as plt
import numpy as np
import cv2
import os

src = './data/'
files = os.listdir(src)
lfw_people = []
for file in files:
    lfw_people.append(cv2.imread(src+file, 0))
lfw_people = np.array(lfw_people)

name = ['resized_parvaz.png','resized_mahdieh.jpg']
test = cv2.imread('./img/'+name[0], 0).reshape(1, 64, 64)

print(test.shape)
print(lfw_people.shape)

num_pcs = 15
def pca(X, num_components):
    mean_face = np.mean(X, axis=0)
    X_meaned = X - np.mean(X, axis=0)
    covariance_matrix = np.cov(X_meaned, rowvar=False)
    print(X.shape)
    print(covariance_matrix.shape)
    eigenvalues, eigenvectors = np.linalg.eigh(covariance_matrix)
    sorted_index = np.argsort(eigenvalues)
    sorted_eigenvectors = eigenvectors[:, sorted_index]
    eigenvector_subset = sorted_eigenvectors[:, :num_components]
    X_reduced = np.dot(X_meaned, eigenvector_subset)
    return X_reduced, eigenvector_subset, mean_face

# TRAINING
mnist_reduced, eigenvector_subset, mean_face = pca(lfw_people.reshape(-1, 64*64), num_pcs)

plt.figure(figsize=(12, 8))
grid_cols = 5  # Adjust grid columns
grid_rows = (num_pcs + 1) // grid_cols + 1  # Adjust grid rows dynamically

plt.subplot(grid_rows, grid_cols, 1)
plt.title("Mean Face")
plt.imshow(mean_face.reshape(64,64), cmap="gray")
plt.axis("off")

# Plot eigenfaces
for i in range(num_pcs):
    plt.subplot(grid_rows, grid_cols, i + 2)
    plt.title(f"Eigenface {i + 1}")
    log_image = np.log1p(eigenvector_subset[:, i].reshape(64,64))
    log_image = np.uint8(log_image / log_image.max() * 255)
    plt.imshow(log_image, cmap="gray")
    plt.axis("off")

plt.tight_layout()
plt.show()


# TESTING
test_reduced = np.dot(test.reshape(-1, 64*64), eigenvector_subset)
print(eigenvector_subset.shape)
# plt.figure(figsize=(8, 6))
# scatter = plt.scatter(mnist_reduced[:, 0], mnist_reduced[:, 1], c=labels, cmap='tab10', alpha=0.7)
# plt.colorbar(scatter)
# plt.xlabel('PC1')
# plt.ylabel('PC2')
# plt.show()

mnist_decompressed = np.dot(mnist_reduced, eigenvector_subset.T) + np.mean(lfw_people.reshape(-1, 64*64), axis=0)
test_decompressed = np.dot(test_reduced, eigenvector_subset.T)

def visualize_decompression(original, decompressed, img_shape, num_images=13, title=""):
    original = original.reshape(-1, *img_shape)
    decompressed = decompressed.reshape(-1, *img_shape)

    plt.figure(figsize=(10, 4))

    for i in range(num_images):
        plt.subplot(2, num_images, i + 1)
        plt.imshow(original[i])
        plt.axis('off')

        plt.subplot(2, num_images, num_images + i + 1)
        log_image = np.log1p(decompressed[i])
        plt.imshow(log_image)
        plt.axis('off')

    plt.tight_layout()
    plt.show()


visualize_decompression(lfw_people, mnist_decompressed, (64, 64), title="PCA Decompression")
visualize_decompression(test, test_decompressed, (64, 64), num_images=1, title="PCA Decompression")

مراجع

[1] M. Soleymani Baghshah, “Machine learning.” Lecture slides.

[2] B. Póczos, “Advanced introduction to machine learning.” Lecture slides. CMU-10715.

[3] M. Gormley, “Introduction to machine learning.” Lecture slides. 10-701.

[4] M. Gormley, “Introduction to machine learning.” Lecture slides. 10-301/10-601.

[5] F. Seyyedsalehi, “Machine learning and theory of machine learning.” Lecture slides. CE-477/CS-828.

[6] G. Strang, “Linear algebra and its applications,” 2000.

our proposed

Proposed Mathematical Formulation: Denoising-Enhanced Semantic Projection for Robust Retrieval

1. Problem Formulation

Let $\mathcal{D} = {d_1, d_2, \ldots, d_N}$ represent a corpus of text documents, where each document $d_i$ may be corrupted by noise $\eta_i$, yielding the observed noisy document $\tilde{d}_i = d_i + \eta_i$. This noise may manifest as informal language, abbreviations, typographical errors, or other perturbations that degrade semantic coherence.

In a standard RAG pipeline, a pre-trained encoder model $\mathcal{E}: \mathcal{X} \to \mathbb{R}^m$ maps a document to a high-dimensional embedding vector $\mathbf{x}_i = \mathcal{E}(\tilde{d}_i) \in \mathbb{R}^m$, where $m$ is typically large (e.g., 1024 or 3072). The retrieval function $\mathcal{R}(\mathbf{q}, {\mathbf{x}_i})$ then computes the similarity between a query embedding $\mathbf{q} = \mathcal{E}(q)$ and the corpus embeddings ${\mathbf{x}_i}$ to retrieve the most relevant documents.

The core problem we address is that the noise $\eta_i$ in $\tilde{d}_i$ induces a perturbation $\boldsymbol{\epsilon}_i$ in the embedding space, such that $\mathbf{x}_i = \mathbf{x}_i^* + \boldsymbol{\epsilon}_i$, where $\mathbf{x}_i^* = \mathcal{E}(d_i)$ is the ideal, noise-free embedding. This perturbation misaligns the embeddings from their true semantic positions, leading to suboptimal retrieval performance.

2. Proposed Denoising-Enabled Embedding Projection

We propose to learn a Denoising Projection Layer $\mathcal{P}: \mathbb{R}^m \to \mathbb{R}^k$, which maps the noisy, high-dimensional embedding $\mathbf{x}_i$ to a purified, lower-dimensional representation $\mathbf{z}_i \in \mathbb{R}^k$, with $k \ll m$. The objective of $\mathcal{P}$ is to minimize the effect of the noise perturbation while preserving the essential semantic information.

This can be formulated as an optimization problem. Let $\mathbf{X} \in \mathbb{R}^{N \times m}$ be the matrix of noisy embeddings. We seek a projection matrix $\mathbf{W} \in \mathbb{R}^{m \times k}$ such that the projected embeddings $\mathbf{Z} = \mathbf{X} \mathbf{W}$ satisfy:

\[\min_{\mathbf{W}} \quad \underbrace{\left\|\mathbf{X}^* - \mathbf{X} \mathbf{W} \mathbf{W}^\top\right\|_F^2}_{\text{Reconstruction Error}} + \lambda_1 \underbrace{\operatorname{tr}\left(\mathbf{W}^\top \boldsymbol{\Sigma}_\eta \mathbf{W}\right)}_{\text{Noise Suppression}} - \lambda_2 \underbrace{\operatorname{tr}\left(\mathbf{W}^\top \mathbf{X}^\top \mathbf{X} \mathbf{W}\right)}_{\text{Semantic Variance Maximization}}\]

Subject to: $\mathbf{W}^\top \mathbf{W} = \mathbf{I}_k$

Where:

$\mathbf{X}^*$ is the (unobservable) matrix of ideal, noise-free embeddings. In practice, this is approximated using a robust estimator or a contrastive learning objective.
$\boldsymbol{\Sigma}_\eta$ is the covariance matrix of the noise $\boldsymbol{\epsilon}_i$, estimated from a corpus of noisy-clean text pairs or via data augmentation.
The first term aims to reconstruct the clean semantic manifold.
The second term penalizes the projection of directions with high noise variance, actively suppressing noisy components.
The third term acts as a regularizer that encourages the projected space $\mathbf{Z}$ to retain high variance, thereby preserving discriminative semantic features.
The orthogonality constraint $\mathbf{W}^\top \mathbf{W} = \mathbf{I}_k$ ensures the projection does not arbitrarily stretch or shrink the space.

The hyperparameters $\lambda_1, \lambda_2 \geq 0$ control the trade-off between noise removal and information retention. The resulting purified embedding for retrieval is $\mathbf{z}_i = \mathbf{x}_i \mathbf{W}$.

This formulation generalizes classical PCA (which would only consider the third term and the constraint) by explicitly incorporating a noise model, thereby enabling a more principled and targeted approach to building noise-resilient semantic representations for efficient and accurate retrieval.

پایپ‌لاین سبک‌وزن تولید تقویت‌شده با بازیابی مبتنی بر مدل ازپیش‌آموزش‌دیده با قابلیت نویززدایی

چکیده فارسی

مقدمات مورد نیاز

تحلیل مؤلفه‌های اصلی (PCA)

برخی از مزایای کاهش ابعاد

تکنیک‌های کاهش ابعاد

۱. انتخاب ویژگی (Feature Selection)

تعریف ریاضی

مدل ریاضی

تفسیر

۲. استخراج ویژگی (Feature Extraction)

تعریف ریاضی

الف) استخراج خطی

ب) استخراج غیرخطی

نمونه الگوریتم‌ها

کد: مجموعه داده گوسی 2 بعدی

کد: اولین محور PCA

کد: محور اول و دوم

تعریف

تفسیرها

بیشینه کردن واریانس داده‌های تصویر شده

پیش‌زمینه

مقادیر ویژه و بردارهای ویژه چیستند؟

تفسیر هندسی

چگونه مقادیر ویژه و بردارهای ویژه را پیدا کنیم؟

مثال عددی

کوواریانس چیست؟

مثال ماتریس کوواریانس

کد: مثال

کد: مثال

کد: مثال

کد: مثال

بیان واریانس

مسئله بیشینه‌سازی

استفاده از ضرب‌کننده‌های لاگرانژ

تفسیر

کد:

کد:

درک چرخش داده در تحلیل مؤلفه‌های اصلی (PCA)

1. ماتریس کوواریانس و بردارهای ویژه

2. تبدیل داده (چرخش)

3. ماتریس کوواریانس در فضای تبدیل شده

4. مشتق دقیق کوواریانس در فضای تبدیل شده

۵. تفسیر هندسی

کد:

اگر به جای مقادیر ویژه بزرگ از مقادیر ویژه کوچک در پروژه چهره‌های ویژه استفاده کنیم چه اتفاقی می‌افتد؟

کد مربوط به آزمایش با مقادیر ویژه کوچک

(این بخش از کد مشابه کد قبلی است اما با مرتب‌سازی معکوس برای انتخاب مقادیر کوچک)

مراجع

our proposed

Proposed Mathematical Formulation: Denoising-Enhanced Semantic Projection for Robust Retrieval

1. Problem Formulation

2. Proposed Denoising-Enabled Embedding Projection