تشخیص ناهنجاری تک‌کلاسه مبتنی بر پوش‌محدب ضمنی و یادگیری دسته‌جمعی

یوسف قلعه‌نوئی

👤 درباره نویسنده

یوسف قلعه‌نوئی

🎓 کارشناسی ارشد مهندسی کامپیوتر (۱۴۰۱–۱۴۰۴)
🤖 گرایش: هوش‌مصنوعی و رباتیکز
📊 حوزه پژوهشی: تشخیص ناهنجاری و مدل‌های غیرمتمرکز
🏆 درجه فارغ‌التحصیلی: عالی

---

---

🎓 پیام استاد راهنما

«فارغ‌التحصیلی یوسف قلعه‌نوئی با درجه عالی را صمیمانه تبریک می‌گویم. تلاش، پشتکار و خلاقیت ایشان در زمینه‌های تشخیص ناهنجاری و یادگیری غیرمتمرکز، الگوی ارزشمندی برای سایر دانشجویان است. برای آینده‌ی پژوهشی و حرفه‌ای او بهترین موفقیت‌ها را آرزو دارم.»
— دکتر هادی صادقی یزدی، استاد راهنما

---

📬 راه‌های ارتباطی

چکیده

در این پژوهش چارچوبی نوین برای تشخیص ناهنجاری ارائه می‌شود که بر پایه‌ی طبقه‌بندی تک‌کلاسه و بازنمایی پوش محدب ضمنی از ناحیهٔ داده‌های عادی طراحی شده است. ایدهٔ اصلی، برآورد مرز تصمیم به‌صورت غیرصریح و با اتکا به منظم‌سازی تور کشسان است؛ ترکیب همزمان $\ell_1$ و $\ell_2$ در تور کشسان از یک سو به تُنُک‌سازی و انتخاب ویژگی‌های مؤثر می‌انجامد و از سوی دیگر پایداری عددی و اثر گروهی را در میان ویژگی‌های همبسته فراهم می‌کند. برای ارتقای دقت و کاهش سوگیری ناشی از نامتوازنی داده، از یادگیری دسته‌جمعی مبتنی بر نمونه‌برداری و زیرفضای تصادفی بهره گرفته‌ایم. حل مسئله بهینه‌سازی نیز با استفاده از روش‌های گرادیان پروکسیمال و الگوریتم‌های AMP انجام می‌شود. به‌منظور رفع محدودیت‌های همگرایی AMP، نسخه‌ی پیشرفته‌ی آن یعنی KAMP به‌کار گرفته شده است که با ترکیب ایده‌های فیلتر کالمن و AMP، همگرایی را در شرایط نویزی و ماتریس‌های بد‌حالت پایدارتر و سریع‌تر می‌کند. همچنین گونه‌ی توزیع‌شده‌ی آن، DKAMP، با تقسیم ماتریس اندازه‌گیری میان گره‌ها و تبادل پیام‌های کم‌حجم از طریق توپولوژی‌های متنوع گراف، مقیاس‌پذیری و کارایی را در شبکه‌های بزرگ تضمین می‌نماید.
چارچوب پیشنهادی روی مجموعه‌داده‌های مرجع متنوع ارزیابی و با روش‌های مطرحی همچون OCSVM، SVDD، LOF، IF و EE مقایسه شده است. نتایج نشان می‌دهد مدل پیشنهادی نه‌تنها میانگین حسابی و هندسی امتیازها، بلکه شاخص‌هایی مانند دقت، صحت، بازخوانی، F1 و کاپا را به‌طور معناداری بهبود می‌دهد و در برابر ساختارها و توزیع‌های مختلف داده عملکردی پایدار و قابل اعتماد دارد. بدین‌ترتیب، ترکیب پوش محدب ضمنی، منظم‌سازی تور کشسان، AMP،KAMP،DKAMP
و یادگیری دسته‌جمعی چارچوبی منسجم، مقیاس‌پذیر و استوار برای تشخیص ناهنجاری در سناریوهای واقعی و داده‌های پیچیده فراهم می‌آورد.

تعریف مساله

ناهنجاری‌ها الگوهایی در داده‌ها هستند که با یک مفهوم خوب تعریف شده از رفتار عادی مطابقت ندارند. تشخیص ناهنجاری به مشکل یافتن الگوهایی در داده‌ها اشاره دارد که از رفتار عادی مورد انتظار پیروی نمی‌کنند. این الگوهای غیرقابل تطابق معمولاً در زمینه‌های مختلف به عنوان ناهنجاری‌ها ، نقاط پرت، مشاهدات ناهماهنگ و استثناها شناخته می‌شوند. از این میان، ناهنجاری‌ها و نقاط پرت دو اصطلاحی هستند که به طور معمول در زمینه‌های مختلف تشخیص ناهنجاری استفاده می‌شوند و گاهی به طور متناوب به کار می‌روند. اهمیت تشخیص ناهنجاری به این واقعیت برمی‌گردد که ناهنجاری‌ها معمولا به اطلاعاتی برای اقدامات بحرانی تبدیل می‌شوند. بسیاری از سیستم‌های یادگیری ماشین فرض می‌کنند که تجربه آموزشی آنها نماینده‌ای از تجربه آزمون است، اما در دنیای واقعی، این فرض نادرست است؛ داده‌های “نو” یا “ناهنجار” که در داده‌های آموزشی وجود نداشته‌اند، می‌توانند منجر به کاهش دقت پیش‌بینی‌ها و بروز نگرانی‌های ایمنی شوند؛ بعنوان مثال، سیستم‌های خودران باید در صورت مشاهده‌ی شرایط یا اشیاء ناشناخته‌ای که از قبل آموزش ندیده‌اند به انسان‌ها هشدار دهند و یا یک تصویر MRI ناهنجار ممکن است نشان‌دهنده وجود تومورهای بدخیم باشد.
موضوع دیگری که به تشخیص ناهنجاری مربوط می‌شود، تشخیص نوآوری است که هدف آن شناسایی الگوهای قبلاً مشاهده نشده (نوظهور، جدید) در داده‌ها است. تفاوت بین الگوهای جدید و ناهنجاری‌ها این است که الگوهای جدید اغلب ممکن است پس از شناسایی به مدل عادی اضافه ‌شوند.
بعلاوه در شرایط واقعی، به دلیل کاربردهای عملی در شرکت‌ها یا صنایع، داده‌های تولید شده اغلب توزیع نامتوازن دارند؛ به عنوان مثال، مسائلی مانند تشخیص بیماری، تحلیل اختلال‌های بیولوژیکی، پیش‌بینی بلایای طبیعی، تشخیص ناهنجاری، کشف تلقب و همچنین کاربردهای بیومتریکی‌ای مانند احراز هویت دارای مجموعه دادگانی نامتوازن هستند. گرابز در سال 1969 اولین کسی بود که ناهنجاری را به عنوان: “مشاهده بیرونی یا پرت که به وضوح از سایر اعضای نمونه‌ای که در آن رخ می‌دهد منحرف می‌شود” تعریف کرد. بنابراین، یک رویکرد ساده برای تشخیص ناهنجاری این است که یک منطقه نمایانگر رفتار عادی تعریف کنیم و هر مشاهده‌ای در داده که به این منطقه عادی تعلق ندارد را به عنوان یک ناهنجاری اعلام کنیم. اما عوامل مختلفی این رویکرد ظاهراً ساده را به چالشی بزرگ تبدیل می‌کند. بعنوان مثال، در زمینه یادگیری ماشین، به طور معمول فرض می‌شود که تعداد نمونه‌ها در هر کلاس مورد مطالعه، تقریباً برابر است. این در‌حالی است که در مسائل مربوط به تشخیص ناهنجاری که معمولا با داده‌های نامتوازن در ارتباط هستند استفاده از روش‌های مرسوم طبقه‌بندی (دو یا چندکلاسه) منجر به انحراف به سمت کلاس یا کلاس‌هایی می‌شود که نمونه بیشری دارند. در چنین شرایطی که مدل‌سازی و تشخیص نمونه‌های کلاس اقلیت، بسیار دشوار است، استفاده از طبقه‌بند تک کلاسه (OCC) رویکردی مناسب برای تشخیص داده‌های غیرعادی نسبت به داده‌‌های کلاس شناخته شده(اکثریت) می‌باشد. OCC (شکل ۱) یک حالت خاص از دسته‌بندی چندکلاسه است، جایی که داده‌های مشاهده‌شده در طول آموزش تنها از یک کلاس مثبت هستند و کلاس منفی یا وجود ندارد، یا به خوبی نمونه‌برداری نشده و یا به وضوح تعریف نشده است. OCC همچنین در مسائل خاصی مانند داده‌های نویزی، انتخاب ویژگی‌ و کاهش حجم داده‌های کلان مورد بحث و مطالعه قرار می‌گیرد . تشخیص ناهنجاری با استفاده از تحلیل محدب (CA) در قالب طبقه‌بندی تک‌کلاسه (OCC) یک تکنیک مهم برای شناسایی نمونه‌های “نو” یا “ناهنجار” است که کاربرد گسترده‌ای در زمینه‌های مختلف دارد. تحلیل محدب از تکنیک‌های تعیین مرزهای هندسی مجموعه هدف استفاده می‌کند.
تحلیل محدب(پوش محدب) علاوه‌بر پیچیدگی زمانی زیاد $\mathcal{O}(n^{\lfloor\frac{p}{2}\rfloor})$ و مقیاس‌ناپذیری آن، در مواجهه با مجموعه‌های غیرمحدب کارایی کمتری دارد. افزون بر این، بسیاری از روش‌های مبتنی بر پوش محدب در مواجهه با داده‌های چندمدی و غیرمحدب دچار ضعف هستند. از سوی دیگر، اغلب روش‌های OCC به یک مسئلهٔ برنامه‌ریزی درجه‌دو منتهی می‌شوند که حل آن در مقیاس‌های بزرگ بسیار پرهزینه است. برای رفع این محدودیت‌ها، در سال‌های اخیر الگوریتم‌های پیام‌رسانی تقریبی (AMP) به‌عنوان یک روش تکراری کارآمد برای حل مسائل بازسازی سیگنال تبدیل شده‌اند. AMP دارای سرعت همگرایی بالا است، اما تضمین همگرایی آن تنها در شرایط ایده‌آل مانند ماتریس‌های تصادفی زیرگاوسی برقرار است. به‌منظور غلبه بر این محدودیت، نسخهٔ توسعه‌یافته‌ای به نام Kalman-AMP (KAMP) معرفی شده است که با ترکیب ایده‌های فیلتر کالمن و AMP، پایداری و همگرایی الگوریتم را در شرایط نویزی و ماتریس‌های بدحالت بهبود می‌دهد. همچنین برای افزایش مقیاس‌پذیری، نسخهٔ غیرمتمرکز این الگوریتم با نام Distributed KAMP(DKAMP) توسعه داده شده است. در این نسخه، ماتریس اندازه‌گیری بین گره‌های یک گراف توزیع می‌شود و هر گره با اجرای محلی الگوریتم KAMP و تبادل اطلاعات با همسایگان (از طریق راهبردهایی نظیر ارتباط تصادفی) به یک برآورد جمعی و مقاوم همگرا می‌شود. این طراحی امکان استفاده عملی از روش‌های مبتنی بر AMP و KAMP را در محیط‌های گرافی بزرگ و پویا فراهم می‌کند و نسبت به نویز و ساختارهای پیچیده داده مقاوم است. به طور خلاصه، مسئلهٔ مورد بررسی در این پژوهش را می‌توان چنین بیان کرد: طراحی و توسعهٔ یک چارچوب طبقه‌بندی تک‌کلاسه مبتنی بر مرز پوش محدب ضمنی که با استفاده از الگوریتم‌های تکراری کارآمد (AMP) و توسعه‌های آن (KAMP و DKAMP) بتواند چالش‌های مربوط به محاسبهٔ پوش محدب، مقیاس‌پذیری، پایداری در شرایط نویزی و داده‌های بدحالت را برطرف سازد.

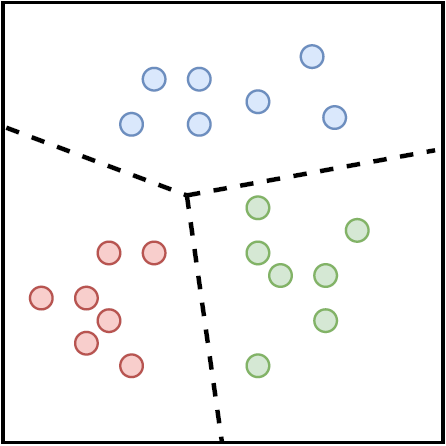
(آ) طبقه‌بندی چند‌کلاسه

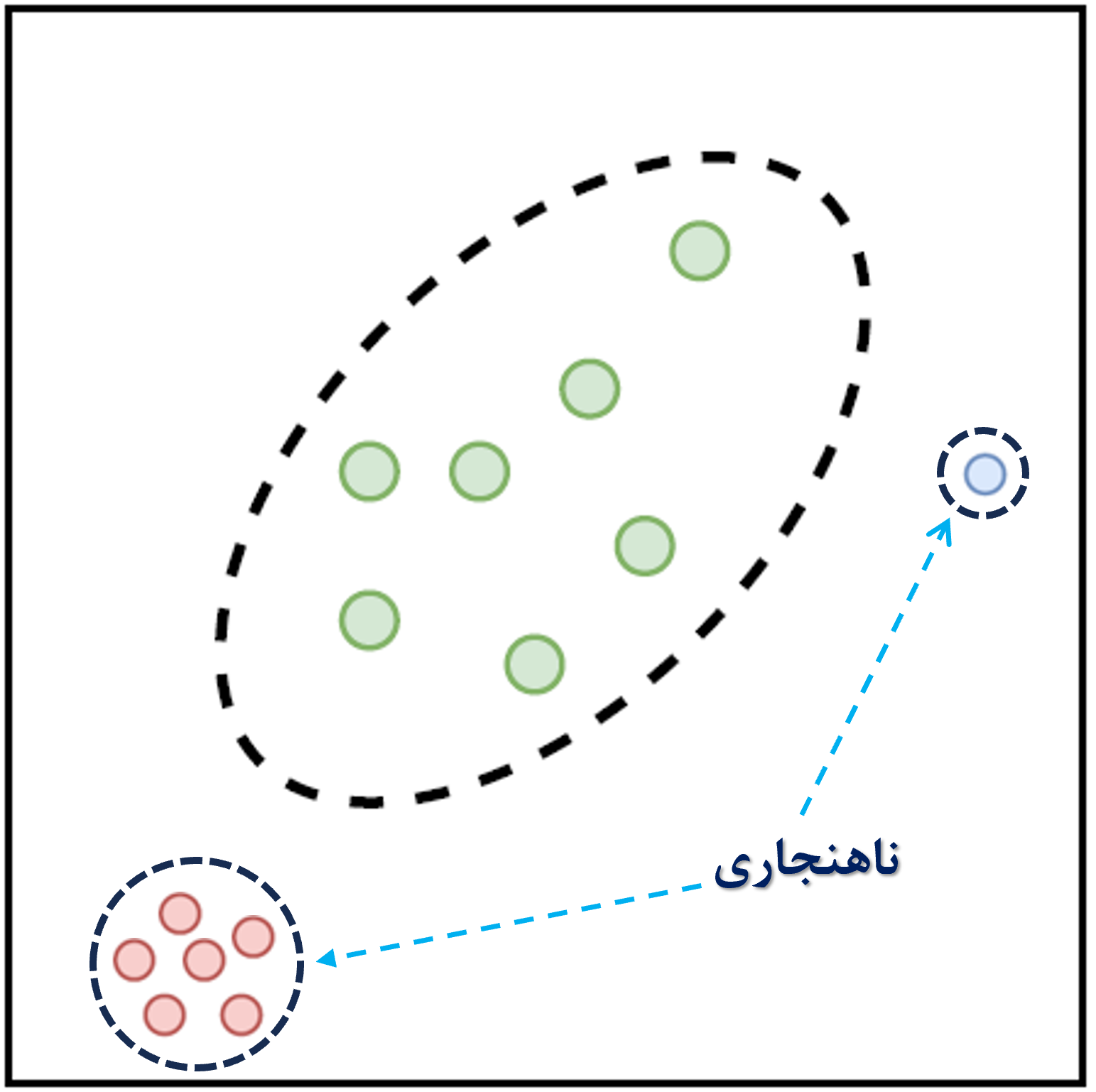
(ب) طبقه‌بندی تک‌کلاسه

شکل 1: تفاوت بین طبقه‌بند تک‌کلاسه و چند‌کلاسه

قسمتی از پیشینه‌تحقیق بررسی شده

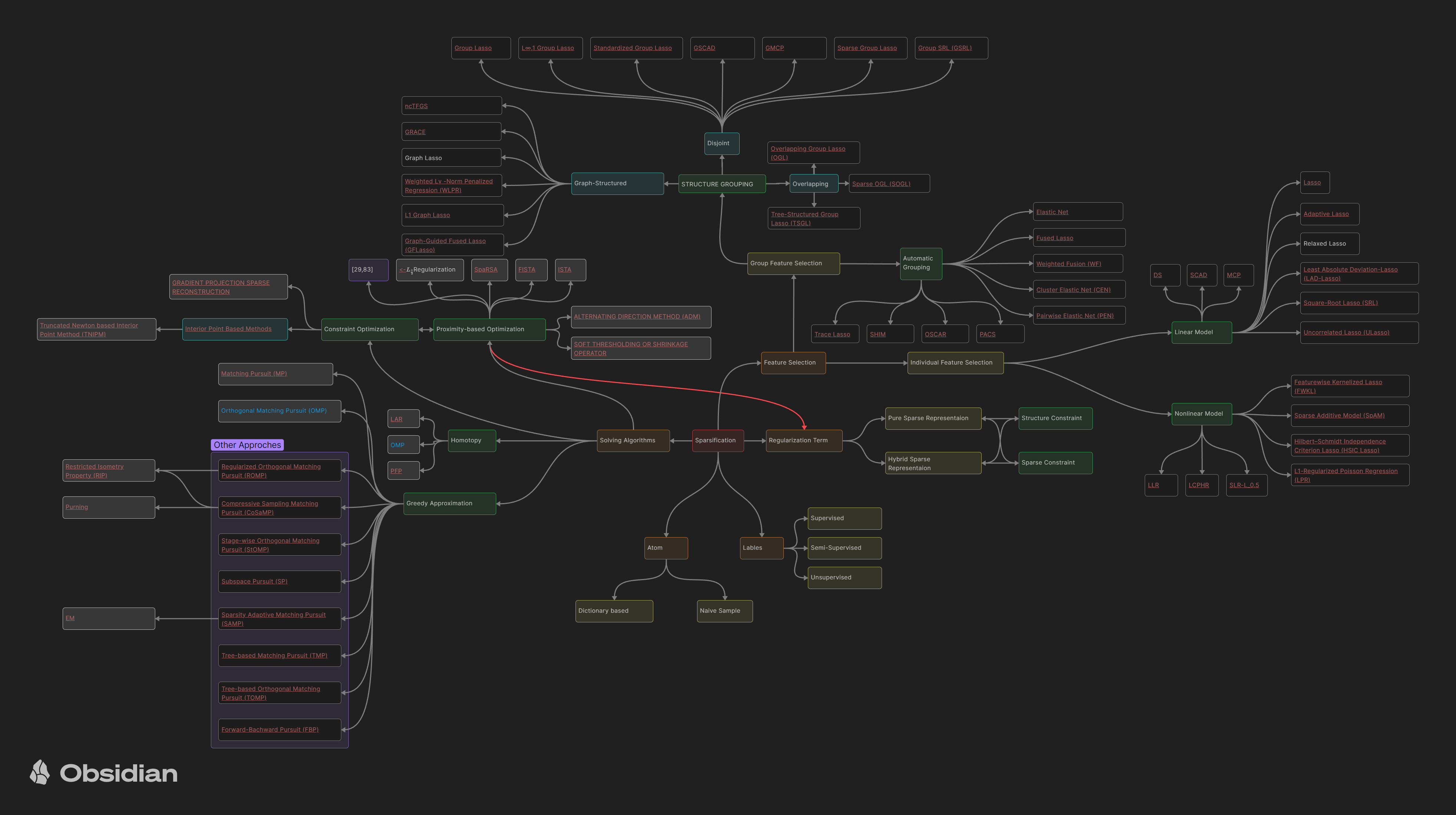
بخشی از پیشینه‌تحقیق مربوط به روش‌های تُنُک‌سازی

مبانی نظری

معرفی الگوریتم‌های پروکسیمال

الگوریتم‌های پروکسیمال (Proximal Algorithms) دسته‌ای از روش‌های بهینه‌سازی برای حل مسائل محدب هستند. این الگوریتم‌ها مشابه جایگاه روش نیوتن در مسائل هموار و کوچک، به‌عنوان ابزاری استاندارد برای مسائل غیرهموار، مقید، بزرگ‌مقیاس و توزیع‌شده مطرح می‌شوند.

مزیت اصلی این روش‌ها توانایی آن‌ها در برخورد با داده‌های بزرگ و ابعاد بالا است. عمل پایه‌ای در این الگوریتم‌ها محاسبه عملگر پروکسیمال است که معادل حل یک مسئله کوچک بهینه‌سازی محدب می‌باشد. این زیرمسئله‌ها اغلب جواب بسته دارند یا با روش‌های ساده و سریع حل می‌شوند.

1.1 تعریف

اگر $f: \mathbb{R}^n \to \mathbb{R} \cup {+\infty}$ یک تابع محدب باشد، عملگر پروکسیمال آن به‌شکل زیر تعریف می‌شود:

\(\text{prox}_{\lambda f}(v) = \arg\min_x \Big( f(x) + \tfrac{1}{2\lambda}\|x - v\|_2^2 \Big)\) این تعریف تضمین می‌کند که برای هر بردار $v$ یک جواب یکتا وجود دارد.

1.2 تفسیرها

• دید هندسی: عملگر پروکسیمال نقطه $v$ را به سمت مجموعه مینیمم تابع $f$ حرکت می‌دهد و در واقع یک مصالحه بین نزدیک بودن به $v$ و کم کردن مقدار $f(x)$ برقرار می‌کند.
• ارتباط با طرح‌ریزی: اگر $f$ تابع نشانگر یک مجموعه محدب باشد، عملگر پروکسیمال دقیقا همان تصویر‌کردن روی آن مجموعه است.
• دید پویا: پروکسیمال را می‌توان شبیه یک گام در روش‌های پویای تکراری دید که مسیر بهینه را دنبال می‌کند.

1.3 نمونه‌ها

چند نمونه مهم از عملگرهای پروکسیمال که به‌وفور در کاربردها دیده می‌شوند:

• تابع $\ell_2$: پروکسیمال آن به‌سادگی یک ضرب مقیاسی روی بردار است.
• تابع $\ell_1$: پروکسیمال آن همان عملگر soft-thresholding است که برای ایجاد تُنُکی (sparsity) به‌کار می‌رود.
• تابع نشانگر یک مجموعه: پروکسیمال برابر با تصویر‌کردن روی آن مجموعه است.
• ترکیب‌های مختلف: با جمع توابع محدب مختلف، پروکسیمال می‌تواند رفتارهای پیچیده‌تر ایجاد کند.

خواص عملگرهای پروکسیمال

در این بخش خواص پایه ای عملگرهای پروکسیمال بررسی می شود. این خواص در تحلیل همگرایی الگوریتم ها و طراحی روش های محاسبه عملگرها نقش کلیدی دارند.

2.1 خاصیت جمع جدایی پذیر

اگر تابع f روی متغیرها جدایی پذیر باشد، یعنی به شکل
$f(x, y) = \varphi(x) + \psi(y)$
نوشته شود، آنگاه عملگر پروکسیمال نیز جدا می شود:

\[\text{prox}_f(v, w) = (\text{prox}_\varphi(v), \text{prox}_\psi(w))\]

در حالت کلی تر، اگر $f(x) = \sum_{i=1}^n f_i(x_i)$ باشد، آنگاه مؤلفه i ام پروکسیمال برابر است با:

\[(\text{prox}_f(v))_i = \text{prox}_{f_i}(v_i)\]

این خاصیت اجازه می دهد که عملگرهای پروکسیمال برای توابع بزرگ به صورت موازی و مستقل محاسبه شوند.

2.2 عملیات پایه

چند خاصیت مهم که امکان بازنویسی پروکسیمال ها را می دهد:

• پس ترکیب:
  اگر $f(x) = \alpha \varphi(x) + b$ با $\alpha > 0$ ، آنگاه
  \(\text{prox}_{\lambda f}(v) = \text{prox}_{\alpha \lambda \varphi}(v)\)

• پیش ترکیب:
  اگر $f(x) = \varphi(\alpha x + b)$، داریم

  \[\text{prox}_{\lambda f}(v) = \tfrac{1}{\alpha}\Big(\text{prox}_{\alpha^2 \lambda \varphi}(\alpha v + b) - b\Big)\]

• اگر $f(x) = \varphi(Qx)$ و Q ماتریس متعامد باشد

  \[\text{prox}_{\lambda f}(v) = Q^T \text{prox}_{\lambda \varphi}(Qv)\]

• افزودن جمله خطی:
  اگر $f(x) = \varphi(x) + a^T x + b$، آنگاه

  \[\text{prox}_{\lambda f}(v) = \text{prox}_{\lambda \varphi}(v - \lambda a)\]

• تنظیم سازی درجه دوم:
  اگر $f(x) = \varphi(x) + \tfrac{\rho}{2}|x-a|^2$، پروکسیمال با تغییر وزن و جابه جایی قابل محاسبه است

\(\text{prox}_{\lambda f}(v) = \text{prox}_{\bar{\lambda} \varphi}\big((\bar{\lambda}/\lambda)v + (\rho \bar{\lambda})a\big),\) که در آن

\[\bar{\lambda} = \tfrac{\lambda}{1 + \lambda \rho}.\]

این نتایج در پردازش تصویر و سیگنال کاربرد زیادی دارند.

2.3 نقاط ثابت

یک ویژگی اساسی این است که $x^\star$ مینیمم تابع f است اگر و فقط اگر

\[x^\star = \text{prox}_f(x^\star)\]

به بیان دیگر، نقاط بهینه همان نقاط ثابت عملگر پروکسیمال هستند. این ارتباط پایه ای بسیاری از الگوریتم های پروکسیمال بر مبنای تکرار نقطه ثابت را توجیه می کند.

2.4 خاصیت انقباضی قوی

عملگر پروکسیمال منقبض قوی است. یعنی برای هر $x, y$ داریم:

\[\|\text{prox}_f(x) - \text{prox}_f(y)\|^2 \leq (x - y)^T(\text{prox}_f(x) - \text{prox}_f(y))\]

این خاصیت پایه ای است که امکان اثبات همگرایی الگوریتم ها را فراهم می کند.

تفسیرهای عملگر پروکسیمال

در این بخش چند دیدگاه مختلف برای درک بهتر عملگرهای پروکسیمال بیان می شود. این تفسیرها نشان می دهند که پروکسیمال‌ها چگونه به مفاهیم آشنا در بهینه سازی و تحلیل ریاضی متصل می شوند.

3.1 منظم سازی مورو ـ یوسیدا (Moreau-Yosida Regularization)

• عملگر پروکسیمال را می توان به عنوان روشی برای هموارسازی توابع محدب دید.
• تعریف منظم سازی مورو ـ یوسیدا:

\[f_\lambda(x) = \min_z \Big( f(z) + \tfrac{1}{2\lambda}\|z - x\|^2 \Big)\]

• این تابع یک تقریب هموار از $f$ است.
• گرادیان این تقریب به صورت زیر داده می شود:

\[\nabla f_\lambda(x) = \tfrac{1}{\lambda}(x - \text{prox}_{\lambda f}(x))\]

• این دیدگاه نشان می دهد که پروکسیمال‌ها می توانند ابزاری برای تعریف توابع هموار و محاسبه گرادیان های پایدار باشند.

3.2 تفسیر بر اساس عملگر تفاضل زیرگرادیان (Resolvent of subdifferential)

• پروکسیمال‌ها را می توان به عنوان معکوس عملگر $(I + \lambda \partial f)$ دید:

\[\text{prox}_{\lambda f} = (I + \lambda \partial f)^{-1}\]

• این تفسیر ارتباط نزدیکی با نظریه عملگرهای اسکالر دارد.
• این دیدگاه توضیح می‌دهد که چرا پروکسیمال‌ها به طور طبیعی با شرایط بهینگی و نظریه نقاط ثابت پیوند دارند.

  3.3 گام گرادیانی اصلاح شده (Modified gradient step)

• پروکسیمال را می توان به عنوان یک گام اصلاح شده گرادیانی دید که شامل جریمه درجه دوم است.
• برای یک تکرار به شکل زیر:

\[x^{+} = \text{prox}_{\lambda f}(x - \lambda \nabla g(x))\]

• این روش شبیه به گرادیان نزولی است ولی برای مسائل غیرهموار و مقید کاربرد دارد.
• نتیجه: پروکسیمال ها همانند گرادیان نزولی عمل می کنند اما پایداری بیشتری در حضور قیود یا اصطلاحات غیرهموار دارند.

3.4 مسئله ناحیه اعتماد (Trust region problem)

• پروکسیمال ها را می توان به عنوان حل یک مسئله بهینه سازی با ناحیه اعتماد در نظر گرفت:

\[\min_z \Big( f(z) + \tfrac{1}{2\lambda}\|z - x\|^2 \Big)\]

• این فرم همانند مسئله ناحیه اعتماد است که در آن یک تابع بهینه سازی در یک کره با شعاع محدود حل می شود.
• به بیان دیگر، پروکسیمال ها مانند یک محدودیت ناحیه اعتماد عمل می کنند که حرکت ها را به اطراف نقطه فعلی محدود می سازد.

الگوریتم های پروکسیمال

4.1 روش گرادیان پروکسیمال

این روش برای حل مسائل بهینه سازی به فرم زیر به کار می رود:

\[\min_x f(x) + g(x)\]

که در آن $f$ یک تابع هموار با گرادیان لیپشیتز است و $g$ یک تابع محدب (ممکن است غیرهموار) باشد.
ایده اصلی این است که یک گام گرادیان روی $f$ و سپس یک گام پروکسیمال روی $g$ انجام می شود:

\[x^{k+1} = \text{prox}_{\lambda g}(x^k - \lambda \nabla f(x^k))\]

• این روش را می توان به عنوان یک نقطه ثابت از عملگر forward-backward دید.
• شرط همگرایی این است که $\lambda \in (0, 1/L]$ باشد که $L$ ثابت لیپشیتز گرادیان $f$ است.
• تفسیرها:
  • به صورت الگوریتم majorization-minimization: در هر گام یک تقریب بالای محدب از $f$ ساخته می شود و سپس کمینه می گردد.
  • به صورت جریان گرادیانی: می توان آن را یک تقریب عددی از جریان گرادیان ترکیبی $f+g$ دانست.
• حالت های خاص:
  • اگر $g$ تابع نشانگر یک مجموعه باشد، الگوریتم به روش projection gradient کاهش می یابد.
  • اگر $f=0$ شود، این همان کیمنه‌سازی پروکسیمال است.
  • اگر $g=0$ شود، الگوریتم به گرادیان نزولی استاندارد تبدیل می شود.

4.2 روش گرادیان پروکسیمال شتاب یافته

این بخش بر پایه روش های شتاب یافته درجه اول بنا شده است (مانند الگوریتم نسترُف).
هدف اصلی افزایش سرعت همگرایی از $O(1/k)$ به $O(1/k^2)$ است.

ایده ها:

• تعریف یک دنباله کمکی $y^k$ که ترکیبی خطی از نقاط گذشته است.
• اجرای گام پروکسیمال روی $y^k$ به جای $x^k$.
• انتخاب پارامترهای ترکیب به گونه ای که سرعت همگرایی بهبود یابد.

\(y^{k+1} := x^k + \omega^k (x^k - x^{k-1})\) \(x^{k+1} := \text{prox}_{\lambda_k g}\Big( y^{k+1} - \lambda^k \nabla f(y^{k+1}) \Big)\)

4.3 روش ضرب کننده های جهت متناوب (ADMM)

ایده اصلی ADMM حل مسائل ترکیبی به شکل:

\[\min_{x,z} f(x) + g(z) \quad \text{s.t. } x = z\]

• با وارد کردن قید اجماع $x=z$ و استفاده از لاگرانژین افزوده، به یک الگوریتم تکراری می رسیم:
  1. به روزرسانی $x$ با کمینه سازی تابع لاگرانژین افزوده.
  2. به روزرسانی $z$ مشابه.
  3. به روزرسانی متغیر دوگان با استفاده از خطای اجماع.

ویژگی ها:

• وقتی $g$ یک مجموعه را نمایش دهد، پروکسیمال $g$ همان projection روی مجموعه است.
• یکی از تفسیرهای مهم ADMM این است که مانند کنترل انتگرالی یک سیستم دینامیکی عمل می کند که با بازخورد خطای انباشته، اجماع را برقرار می کند.
• همچنین می توان آن را به عنوان فرم گسسته جریان saddle-point دید که به نقاط بهینه همگرا می شود.
  \(x^{k+1} := \text{prox}_{\lambda f}(z^k - u^k)\) \(z^{k+1} := \text{prox}_{\lambda g}(x^{k+1} + u^k)\) \(u^{k+1} := u^k + x^{k+1} - z^{k+1}\)

الگوریتم های موازی و توزیع شده

5.1 ساختار مسئله

هدف این بخش ارائه الگوریتم های پروکسیمال موازی و توزیع شده برای حل مسائل بهینه سازی محدب است. ایده اصلی بر پایه الگوریتم ADMM است و بر این اصل بنا شده که می توان تابع هدف یا قیود را به اجزایی تقسیم کرد که حداقل یکی از آن ها خاصیت جدایی پذیری داشته باشد. این خاصیت اجازه می دهد عملگر پروکسیمال به صورت موازی محاسبه شود.

تعریف جدایی پذیری

فرض کنید $[n] = {1, 2, …, n}$ . برای هر زیرمجموعه $c \subseteq [n]$ ، زیر بردار $x_c \in \mathbb{R}^{|c|}$ شامل مؤلفه های $x \in \mathbb{R}^n$ است که اندیس آن ها در $c$ قرار دارد.

مجموعه $P = {c_1, c_2, …, c_N}$ یک افراز از $[n]$ است اگر اجتماع این زیرمجموعه ها برابر با $[n]$ باشد و هیچ دو زیرمجموعه ای اشتراک نداشته باشند.

یک تابع $f : \mathbb{R}^n \to \mathbb{R}$ را $P$-جدایی پذیر می نامیم اگر بتوان آن را به صورت

\[f(x) = \sum_{i=1}^N f_i(x_{c_i})\]

نوشت، که در آن $f_i : \mathbb{R}^{

c_i

} \to \mathbb{R}$ تنها روی متغیرهای $x$ مربوط به شاخص های درون $c_i$ تعریف شده است.

ویژگی مهم جدایی پذیری این است که عملگر پروکسیمال تابع $f$ را می توان به عملگرهای پروکسیمال هر یک از اجزای $f_i$ تجزیه کرد.

برای هر بردار $v \in \mathbb{R}^n$ داریم:

\[\text{prox}_{\lambda f}(v) = \begin{bmatrix} \text{prox}_{\lambda f_1}(v_{c_1}) \\ \text{prox}_{\lambda f_2}(v_{c_2}) \\ \vdots \\ \text{prox}_{\lambda f_N}(v_{c_N}) \end{bmatrix}\]

ساختار کلی مسئله

حال اگر برای تابع $g$ نیز یک افراز مشابه $Q = {d_1, d_2, …, d_M}$ در نظر بگیریم، می توان مسئله بهینه سازی را به صورت زیر نوشت:

\[\min_x \ \sum_{i=1}^N f_i(x_{c_i}) + \sum_{j=1}^M g_j(x_{d_j}) \quad \quad (5.2)\]

که در آن $f_i : \mathbb{R}^{|c_i|} \to \mathbb{R} \cup {+\infty}$ و $g_j : \mathbb{R}^{|d_j|} \to \mathbb{R} \cup {+\infty}$ .

برای سادگی، از شاخص $i$ برای بلوک های $f$ و از $j$ برای بلوک های $g$ استفاده می کنیم.

الگوریتم ADMM برای فرم مسئله (5.2)

برای حل این مسئله به کمک ADMM، به روزرسانی ها به صورت زیر تعریف می شوند:

\(x^{k+1}_{c_i} := \text{prox}_{\lambda f_i}(z^k_{c_i} - u^k_{c_i})\) \(z^{k+1}_{d_j} := \text{prox}_{\lambda g_j}(x^{k+1}_{d_j} + u^k_{d_j})\) \(u^{k+1} := u^k + x^{k+1} - z^{k+1}\)

در این الگوریتم:

• به روزرسانی $x$ با استفاده از پروکسیمال های $f_i$ انجام می شود.
• به روزرسانی $z$ با استفاده از پروکسیمال های $g_j$ صورت می گیرد.
• متغیر $u$ که نقش دوگان یا متغیر ضرب لاگرانژین را دارد، با خطای اجماع به روز می شود.

این ساختار نشان می دهد که مسئله بزرگ اولیه به چند زیرمسئله کوچک شکسته می شود و هر کدام از این زیرمسئله ها را می توان به صورت موازی و مستقل حل کرد.

🔗 منابع پیشنهادی برای یادگیری عمیق‌تر

برای درک بهتر رویکردهای آماری و پیوند آن‌ها با بهینه‌سازی و مدل‌سازی، منابع زیر توصیه می‌شوند:

• Bayes Rules! An Introduction to Applied Bayesian Modeling
  وب‌سایتی جامع و روان که مفاهیم پایه‌ای بیزین را به شکلی کاربردی آموزش می‌دهد. از اصول مقدماتی استنباط بیزین تا مباحث پیشرفته‌تری مانند رگرسیون، طبقه‌بندی و مدل‌های سلسله‌مراتبی را با مثال‌ها و تمرین‌های عملی پوشش می‌دهد.

• Statistics & Data Analysis – Video Series by Steven Brunton (@eigensteve)
  مجموعه‌ای آموزشی در ۳۵ قسمت (حدود ۱۰ ساعت) که مباحث کلیدی آمار و تحلیل داده‌ها را به صورت نظام‌مند ارائه می‌کند؛ از نمونه‌گیری تصادفی و قضیه حد مرکزی تا برآورد توزیع‌ها، روش لحظه‌ها، بیشینه درست‌نمایی، آزمون فرض، نمونه‌گیری مونت‌کارلو و مبانی استنباط بیزین.

• یادداشت‌های آمار نظری
  یک منبع جامع و ارزشمند برای پژوهشگران و دانشجویان علاقه‌مند به مبانی ریاضی آمار.

الگوریتم پیشنهادی

الگوریتم پیام‌رسانی تقریبی مبتنی‌بر کالمن

نسخه غیرمتمرکز روش پیشنهادی

برای پیاده‌سازی الگوریتم‌هایی نظیر AMP و نسخه‌ی توسعه‌یافته‌ی آن KAMP (یا KAMP) به شکل غیرمتمرکز، شبکه‌ای از گره‌ها را می‌توان به‌صورت یک گراف جهت‌دار

\((\mathcal{G}=(\mathcal{V},\mathcal{E}))\) مدل کرد که

\[|\mathcal{V}| = L\]

تعداد گره‌ها است. هر گره $l$ مجموعه‌ای از مشاهدات محلی شامل زیرماتریس

\[(\mathbf{A}_l)\]

و زیربردار

\[(\mathbf{y}_l)\]

را در اختیار دارد، به‌طوری‌که با تجمع این زیرماتریس‌ها و بردارها، ماتریس اندازه‌گیری و بردار مشاهده‌ی کلی به‌دست‌می‌آید:

\[\mathbf{A} = \begin{bmatrix} \mathbf{A}_1 \\ \mathbf{A}_2 \\ \vdots \\ \mathbf{A}_L \end{bmatrix}, \qquad \mathbf{y} = \begin{bmatrix} \mathbf{y}_1 \\ \mathbf{y}_2 \\ \vdots \\ \mathbf{y}_L \end{bmatrix},\]

که در آن

\[(\mathbf{y}_\ell = \mathbf{A}_\ell \mathbf{x} + \boldsymbol{\omega}_\ell)\]

مدل مشاهده‌ی محلی گره

\[(\ell)\]

است (بردار نویز

\[(\boldsymbol{\omega}_\ell)\]

نیز دارای واریانس \((\sigma^2)\) می‌باشد). بنابراین هر گره فقط بخشی از معادله‌ی \((\mathbf{y}=\mathbf{A}\mathbf{x} + \boldsymbol{\omega})\)

را مشاهده می‌کند و نیازی به دانستن کل ماتریس \((\mathbf{A})\)

یا بردار \((\mathbf{y})\) ندارد.

در الگوریتم KAMP توزیع‌شده، هر گره الگوریتم KAMP را روی داده‌های محلی خود اجرا می‌کند و یک تخمین اولیه از بردار $(\mathbf{x})$ به‌دست‌می‌آورد. سپس گره‌ها برای رسیدن به تخمین مشترک، نتایج خود را با همسایگان مبادله می‌کنند. مکانیزم معمول برای این تبادل، میانگین‌گیری اجماعی مقادیر همسایگان است؛ بدین صورت که هر گره $l$ مقدار تخمین خود را با مقادیر دریافتی از همسایگان $(\mathscr{N}_l)$ ترکیب می‌کند.

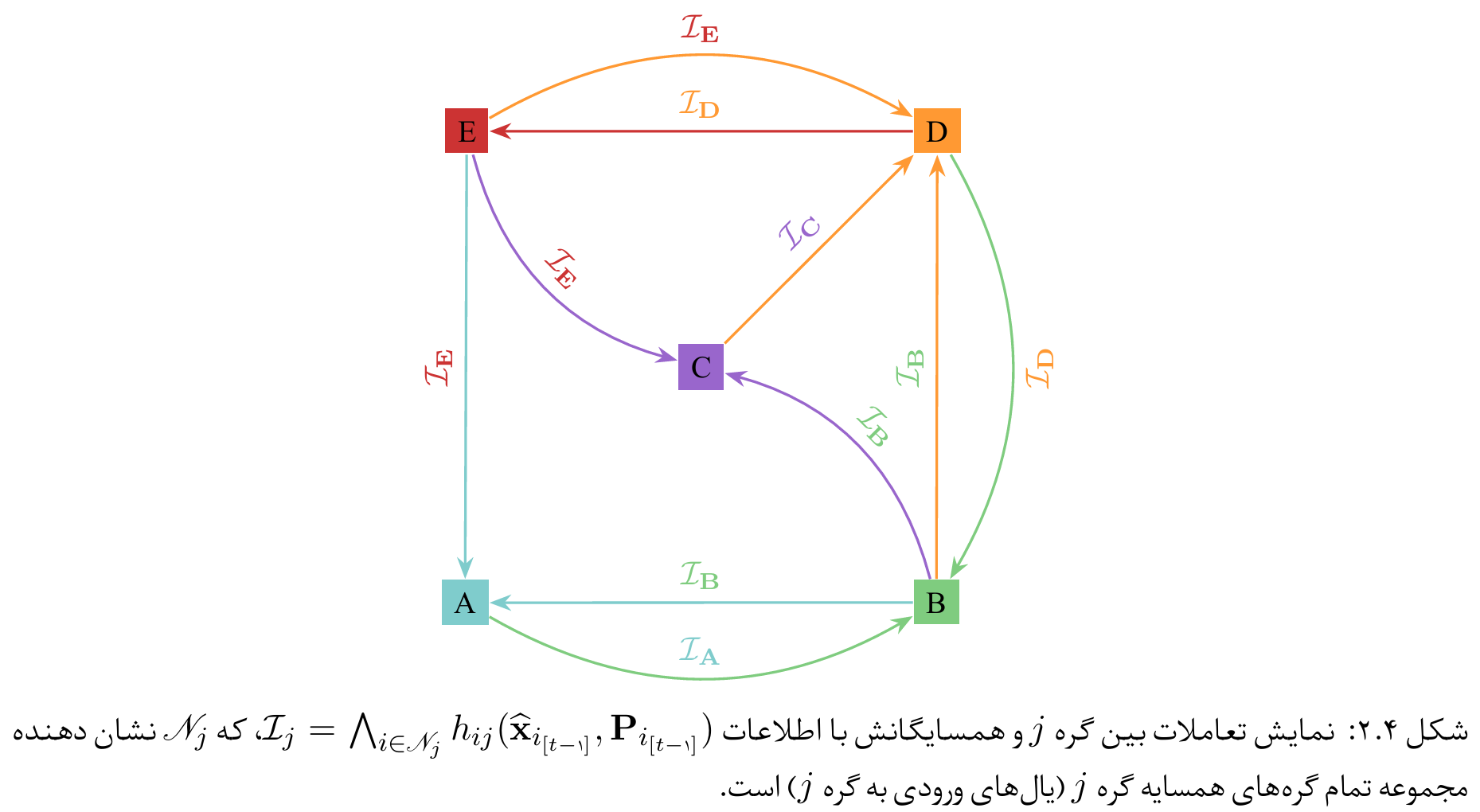
الگوریتم نسخه غیرمتمرکز روش پیشنهادی

الگوریتم غیرمتمرکز پیام‌رسانی تقریبی مبتنی‌بر کالمن

آزمایشات

بررسی کارایی روش پیشنهادی برروی مجموعه دادگان ODDS

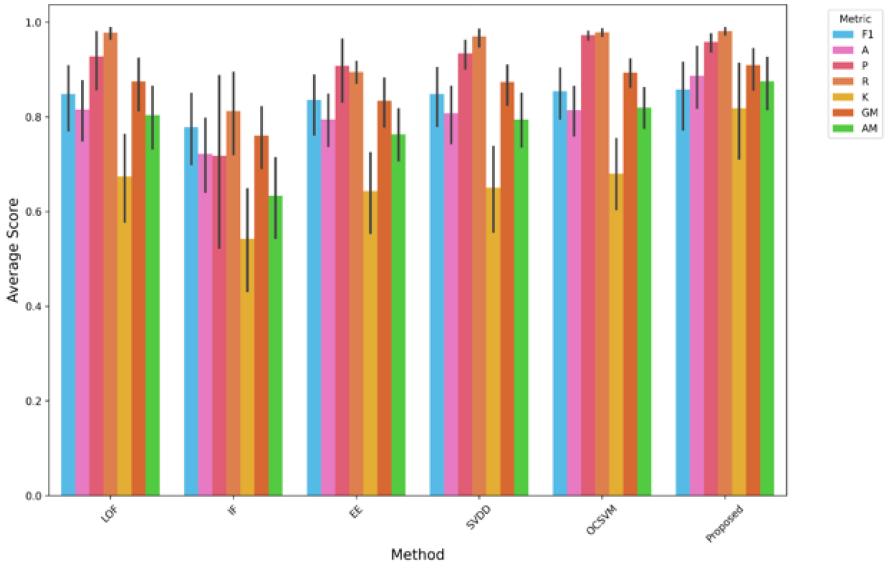
مقایسه معیارهای عملکرد برای مدل‌های مختلف تشخیص ناهنجاری، از جمله LOF، IF، EE، SVDD، OCSVM و روش پیشنهادی. معیارهایی مانند F1-score (F1)، دقت (P)، صحت (A)، بازخوانی (R)، کاپا (K)، میانگین هندسی (GM) و میانگین حسابی (AM) برای ارزیابی اثربخشی هر مدل استفاده می‌شوند. نمودار میله‌ای میانگین نمرات عملکرد را به‌همراه نوار‌های خطا نشان می‌دهد. روش پیشنهادی به طور مداوم نمرات بالایی را در چندین معیار به دست می‌آورد، که عملکرد قوی و قابلیت اطمینان آن را در مقایسه با سایر مدل‌ها نشان می‌دهد.

بررسی عملکرد مرز‌بندی روش‌پیشنهادی برروی داده‌های تصویری

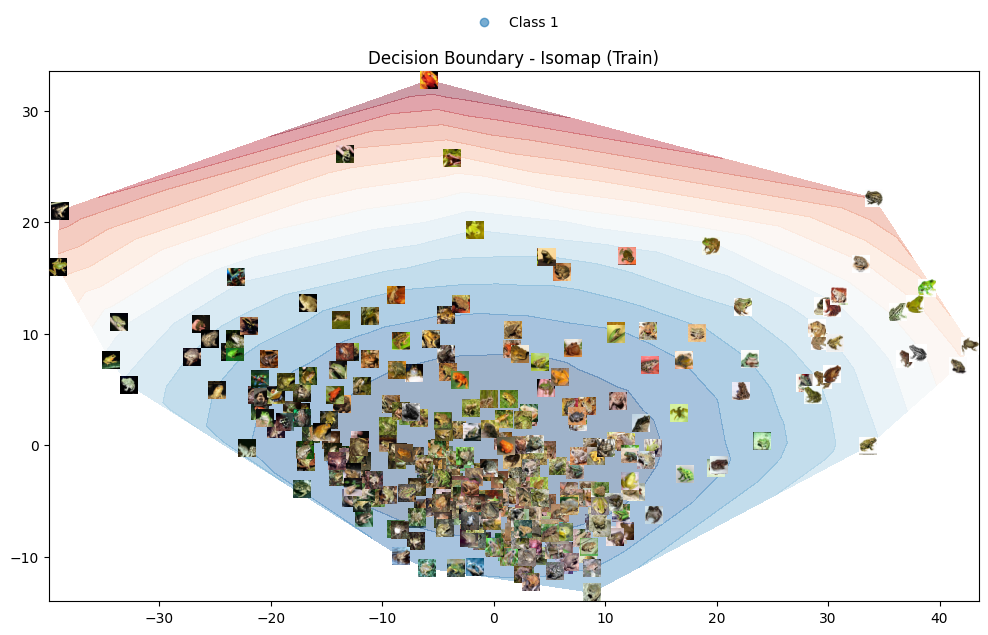
شکل 1: مرز تصمیم‌گیری بر روی کلاس هدف مجموعه داده CIFAR-10 با استفاده از نگاشت Isomap.

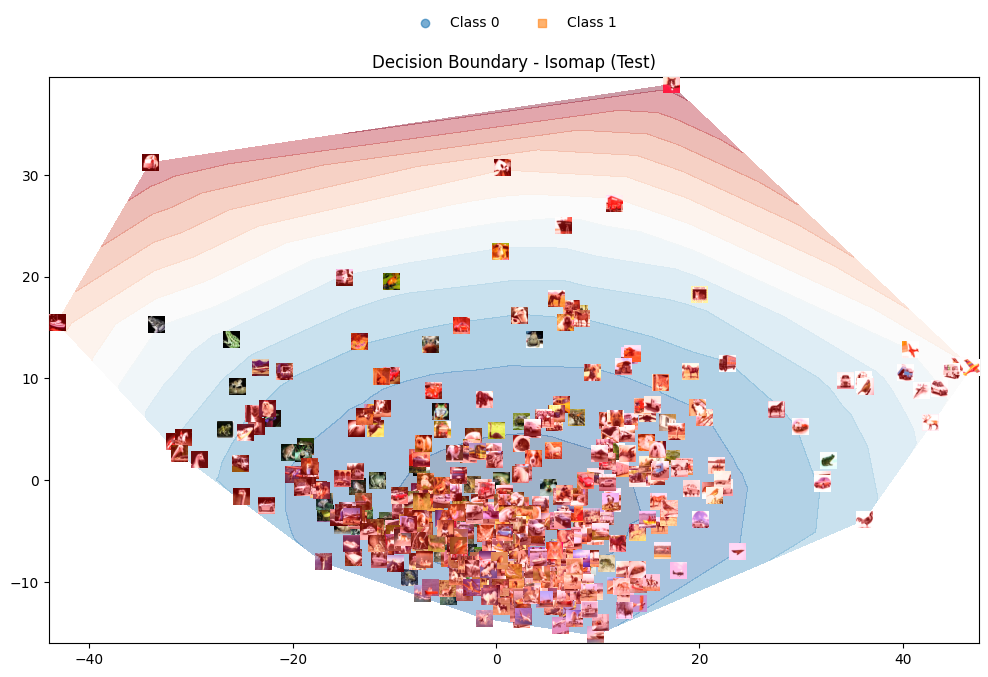
شکل 2: مرز تصمیم‌گیری بر روی دادگان CIFAR-10 با استفاده از نگاشت Isomap (تمامی کلاس‌های مجموعه داده CIFAR-10 استفاده شده است).

بررسی انعطاف‌پذیری روش‌پیشنهادی در فضای ورودی

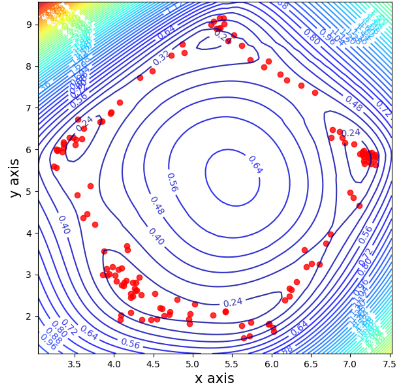
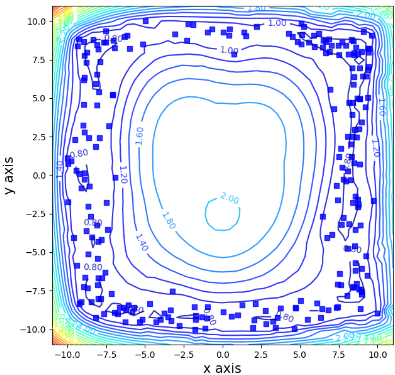
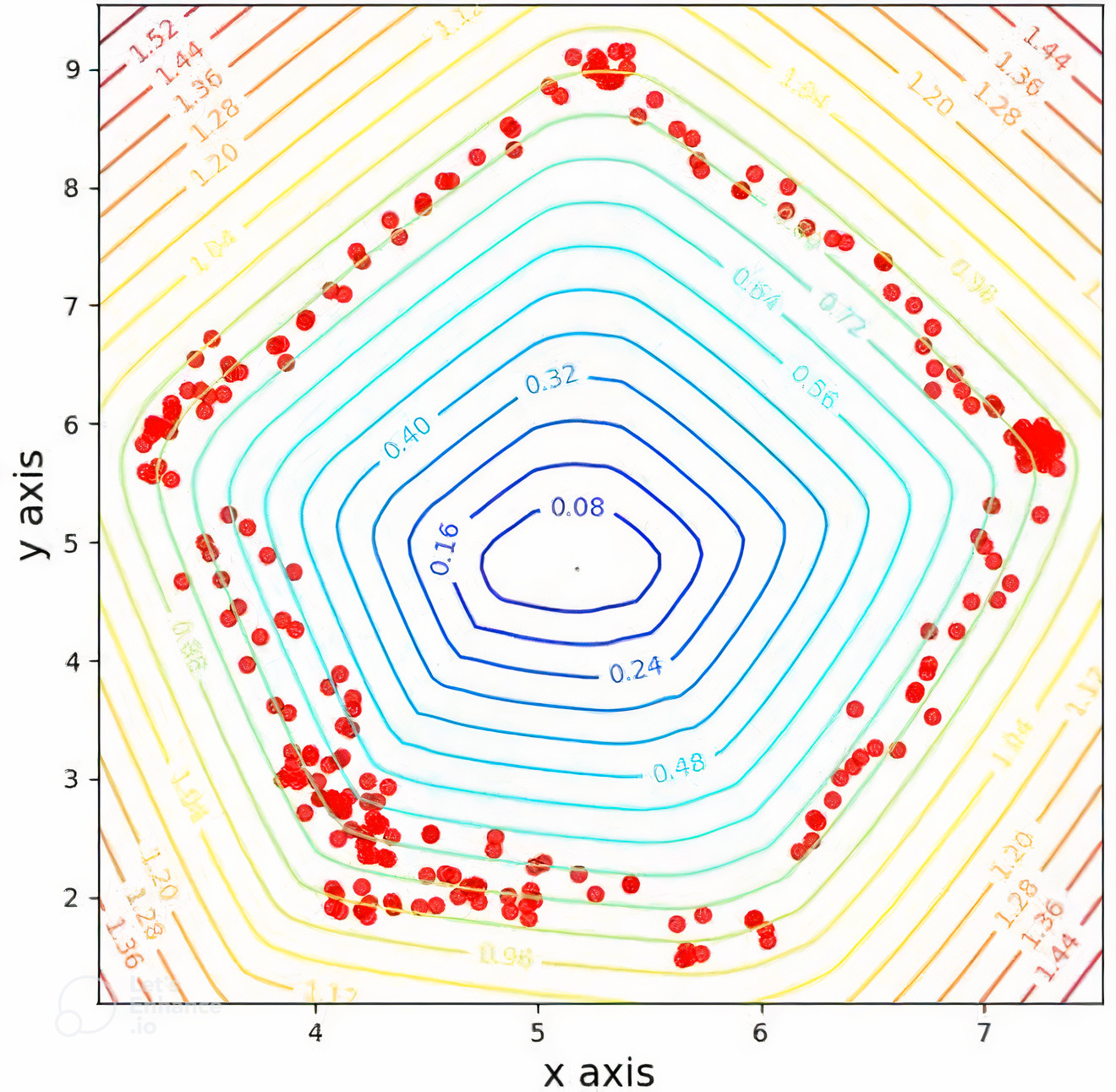
اثبات برتری روش مبتنی‌بر کالمن نسب به پیام‌رسانی تقریبی

شبیه‌سازی‌های انجام شده بر‌روی ماتریس‌های تصادفی گاوسی، متعامد و چوله صورت گرفته‌اند.

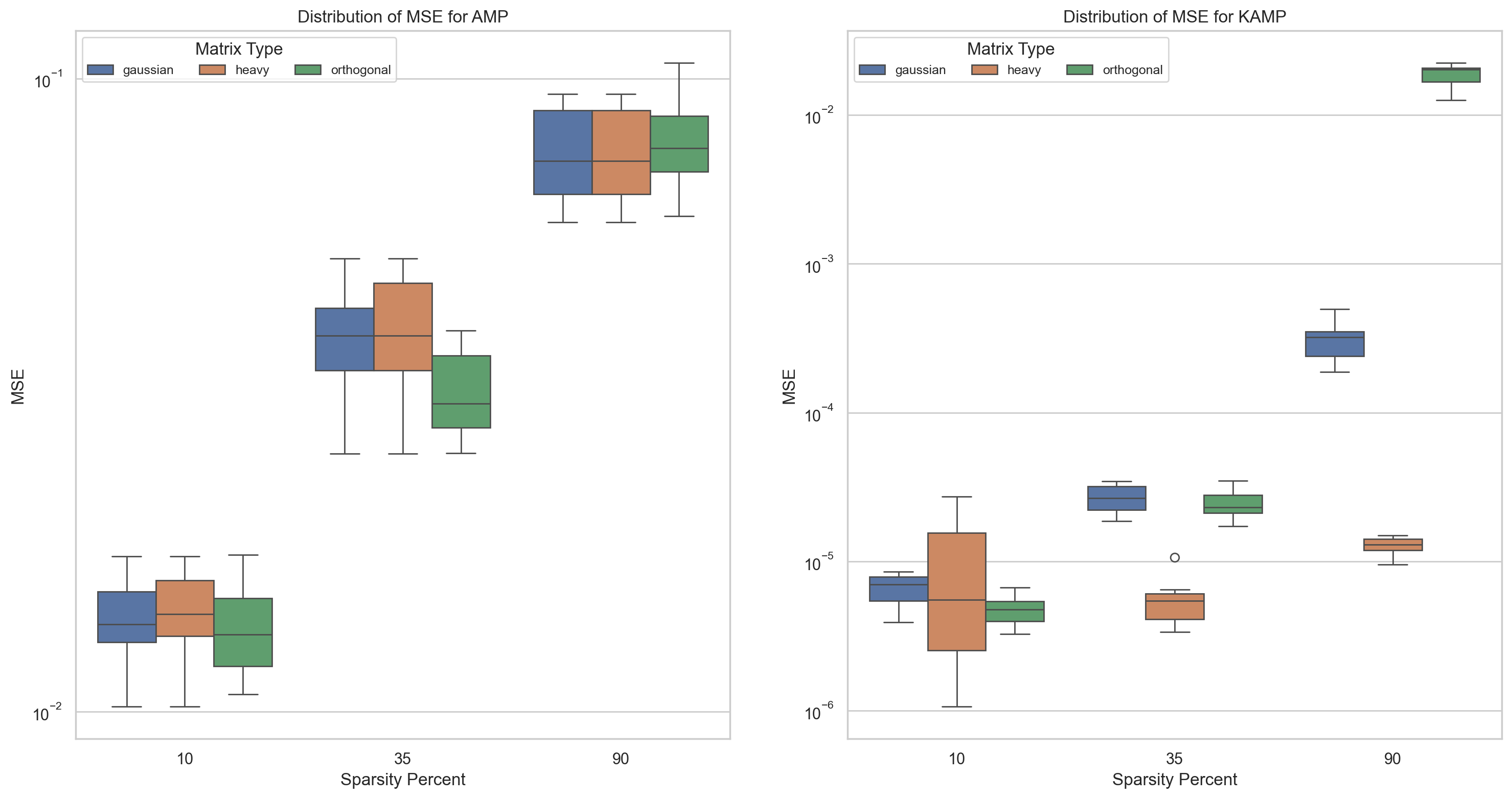
دستیابی نسخه مبتنی‌بر کالمن به کران‌های خطای فشرده‌تر

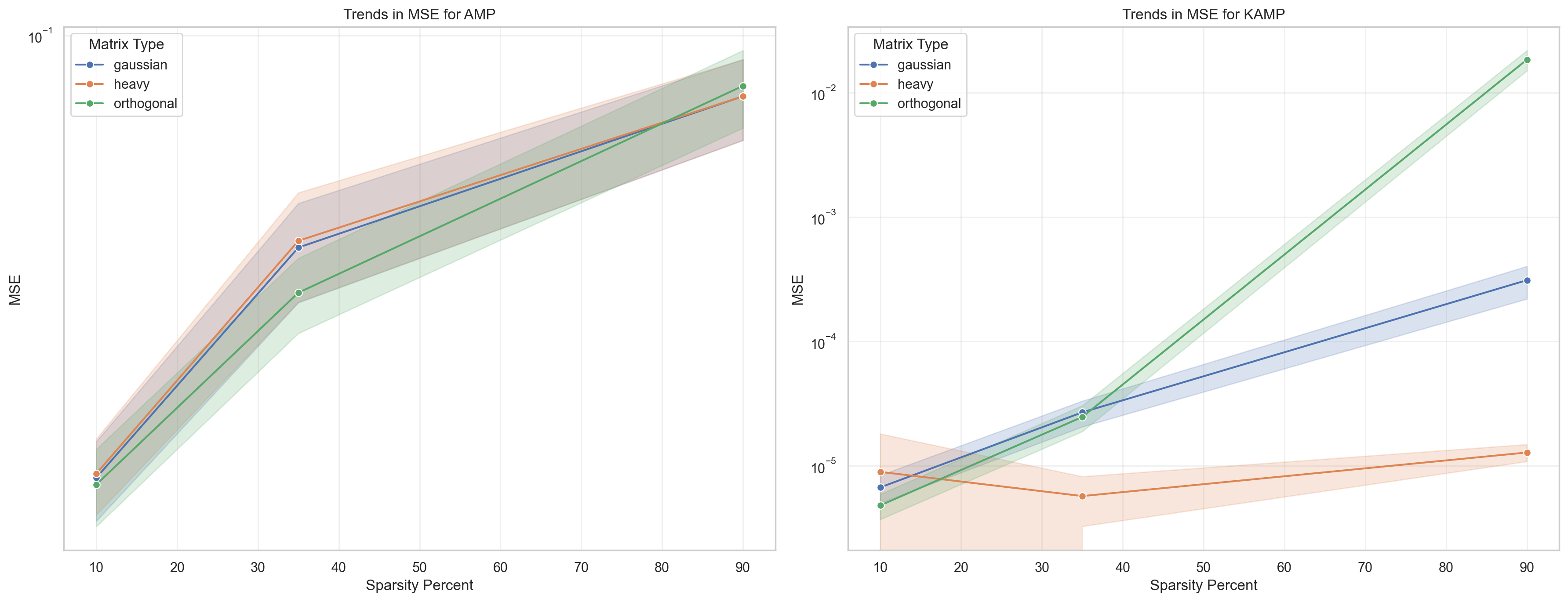
دستیابی نسخه مبتنی‌بر کالمن به واریانس خطای کمتر

جدول ۱: مقایسه میانگین رتبه‌ها و آماره‌های آزمون به تفکیک نوع ماتریس‌ها براساس معیار میانگین مربعات خطا

Matrix Type	Ranks: method	Ranks: N	Ranks: Mean Rank	Test Statistics: Mann-Whitney U	Test Statistics: Wilcoxon W	Test Statistics: Z	Test Statistics: Asymp. Sig. (2-tailed)
Gaussian	AMP	30	45.50	0.000	465.000	-6.653	< 0.001
	KAMP	30	15.50
Heavy	AMP	29	44.72	8.000	473.000	-6.474	< 0.001
	KAMP	30	15.77
Orthogonal	AMP	30	42.73	83.000	548.000	-5.426	< 0.001
	KAMP	30	18.27

جدول ۲: مقایسه میانگین رتبه‌ها و آماره‌های آزمون به تفکیک نوع ماتریس‌ها براساس معیار نسبت سیگنال به نویز

Matrix Type	Ranks: method	Ranks: N	Ranks: Mean Rank	Test Statistics: Mann-Whitney U	Test Statistics: Wilcoxon W	Test Statistics: Z	Test Statistics: Asymp. Sig. (2-tailed)
Gaussian	AMP	30	15.50	0.000	465.000	-6.653	< 0.001
	KAMP	30	45.50
Heavy	AMP	29	15.00	0.000	435.000	-6.595	< 0.001
	KAMP	30	44.50
Orthogonal	AMP	30	15.50	0.000	465.000	-6.653	< 0.001
	KAMP	30	45.50

جدول ۳: مقایسه میانگین رتبه‌ها و آماره‌های آزمون به تفکیک نوع ماتریس‌ها براساس معیار نسبت اوج سیگنال به نویز

Matrix Type	Ranks: method	Ranks: N	Ranks: Mean Rank	Test Statistics: Mann-Whitney U	Test Statistics: Wilcoxon W	Test Statistics: Z	Test Statistics: Asymp. Sig. (2-tailed)
Gaussian	AMP	30	15.50	0.000	465.000	-6.653	< 0.001
	KAMP	30	45.50
Heavy	AMP	29	15.31	9.000	444.000	-6.459	< 0.001
	KAMP	30	44.20
Orthogonal	AMP	30	18.33	85.000	550.000	-5.396	< 0.001
	KAMP	30	42.67

باتوجه به آزمون‌های آماری انجام شده می‌توان دید که روش‌پیشنهادی در تمامی موارد برتری خود نسبت به روش AMP حفظ کرده است.

نمونه‌ای از توپولوژی‌های بررسی شده

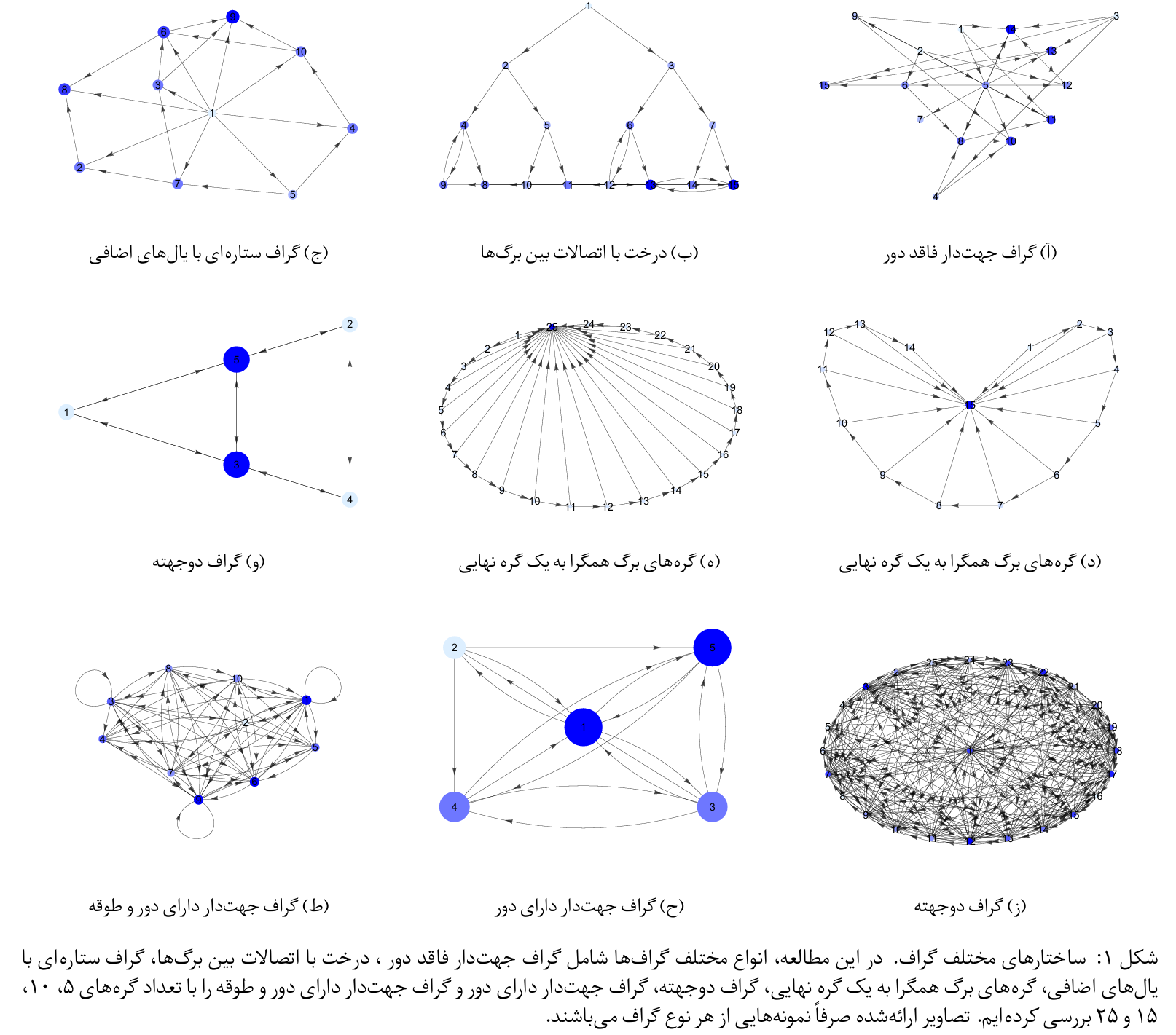
رتبه‌بندی میزان‌کارایی توپولوژی‌های مختلف شبکه براساس معیار‌های سراسری شبکه

نتایج

• برتری روش پیشنهادی در تشخیص ناهنجاری تک‌کلاسه نسبت به روش‌های رقیب بررسی شده
• توانایی تشکیل مرز‌های کاملا منعطف در فضای ورودی
• توانایی تشکیل پوش‌محدب در فضای ویژگی منتانهای با استفاده از کرنل چند‌جمله‌ای
• اثبات کارایی روش KAMP برروی انواع ماتریس‌های تصادفی نسبت به روش AMP
• دستابی با واریانس خطای به مراتب کمتر از واریانس‌خطای AMP

جزییات بیشتر در پایان نامه یوسف قلعه‌نوئی کارشناسی ارشد از دانشگاه فردوسی مشهد