روش‌های تجمعی (Agglomerative Methods) در یادگیری ماشین

نویسنده : عرفان موسوی نژاد

دانشگاه فردوسی مشهد - دانشکده مهندسی - گروه هوش مصنوعی

مقدمه

در مقدمه این مقاله و پیش از ورود به بحث الگوریتم‌های تجمعی، لازم است ابتدا مفاهیم پایه‌ای در تکنیک‌های خوشه‌بندی را درک کنیم. بنابراین، ابتدا به مفهوم خوشه‌بندی (Clustering) در یادگیری ماشین می‌پردازیم: “خوشه‌بندی مجموعه‌ای گسترده از روش‌هاست که هدف آن یافتن زیرگروه‌ها یا خوشه‌هایی در داده‌هاست؛ به‌گونه‌ای که اعضای هر خوشه از نظر ویژگی‌ها یا مشخصه‌های درون‌داده‌ای به یکدیگر شبیه باشند، اما با اعضای خوشه‌های دیگر تفاوت داشته باشند.” اصل اساسی در خوشه‌بندی این است که داده‌های موجود درون یک خوشه باید تا حد ممکن بیشترین شباهت را با یکدیگر داشته باشند و در مقابل، داده‌های خارج از آن خوشه باید بیشترین تفاوت را نسبت به اعضای آن داشته باشند. حال که با دسته‌بندی کلی موضوع آشنایی پیدا کردیم، خوب است بدانیم که در موضوع الگوریتم‌های تجمعی، دو دسته کلی الگوریتم مطرح است:

الگوریتم‌های بر پایه ماتریس: در این نوع الگوریتم، داده‌ها با استفاده از ماتریس فاصله (Distance Matrix) یا ماتریس تشابه (Similarity Matrix) نمایش داده می‌شوند. این ماتریس معمولا مربعی است و اندازه‌ی آن برای n داده، یک ماتریس (n x n) است که در خانه‌ی (i, j)، فاصله و یا شباهت بین نمونه‌ی i و j لحاظ می‌شود.
الگوریتم‌های بر پایه گراف: در این نوع الگوریتم، داده‌ها بصورت گره‌ها (nodes) در یک گراف نمایش داده می‌شوند و یال‌ها (edges) بین هر گره، بیانگر میزان تشابه یا فاصله بین آنها هستند. در این الگوریتم، به جای کار بر روی ماتریس فاصله، مستقیما بر روی ساختار گراف اعمال می‌شود. در این مقاله، تمرکز بر روی الگوریتم‌های بر پایه ماتریس خواهد بود.

تعریف تئوری ماتریس با یک مثال

ماتریس زیر که مرتبط با 5 نقطه در صفحه دکارتی هستند را در نظر بگیرید:

Sample	X	Y
P1	1	1
P2	2	1
P3	5	4
P4	6	5
P5	6.5	6

همانطور که احتمالا میدانید، فاصله اقلیدس (Euclidean Distance) برای دو نقطه در صفحه دکارتی به وسیله فرمول زیر محاسبه می‌شود:

\[d( (x_1,y_1), (x_2,y_2)) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\]

با توجه این فرمول، فاصله هر نقطه با نقطه دیگر محاسبه و داخل ماتریس P(x) قرار میگیرد. بدیهی است که فاصله‌ی هر نقطه تا خودش (قطر اصلی ماتریس) همواره صفر است. در نهایت، ماتریس فاصله برای این داده‌های گفته شده به شکل زیر در خواهد آمد:

\[P(X) = \begin{bmatrix} 0 & 1 & 5 & 6.4 & 7.4 \\ 1 & 0 & 4.2 & 5.7 & 6.7 \\ 5 & 4.2 & 0 & 1.4 & 2.5 \\ 6.4 & 5.7 & 1.4 & 0 & 1.1 \\ 7.4 & 6.7 & 2.5 & 1.1 & 0 \\ \end{bmatrix}\]

دندروگرام (Dendrogram)

نمودار دندروگرام (Dendrogram) که ساختاری درخت‌مانند دارد، روشی موثر برای نمایش توالی خوشه‌هایی است که توسط یک الگوریتم تجمعی تولید می‌شوند. در این ساختار:

هر شی (داده منفرد) با یک گره برگ (leaf node) نمایش داده می‌شود.
هر خوشه (که از ادغام چند داده یا خوشه کوچکتر تشکیل شده است) با یک گره ریشه (root node) نشان داده می‌شود. به بیان دیگر، دندروگرام به ما نشان می‌دهد که چه نقاطی، در چه مراحلی و با چه میزان شباهتی با یکدیگر ادغام شده‌اند. در قسمت پایین، درخت داده‌های منفرد قرار دارند و با بالا رفتن از درخت، خوشه‌های بزرگ‌تر حاصل از ادغام‌های پی‌در‌پی نمایش داده می‌شوند. دندروگرام ماتریس تفاوت برای داده‌های بالا به شکل زیر خواهد بود:

Dendrogram

الگوریتم‌های تجمعی بر پایه تئوری ماتریس – متد اتصال مجرد (Single Link Method)

در آمار، خوشه‌بندی اتصال مجرد یکی از چندین روشِ خوشه‌بندی سلسله‌مراتبی است. این روش بر پایه گروه‌بندی خوشه‌ها به شیوه پایین به بالا (خوشه‌بندی تجمعی) استوار است؛ به‌طوری که در هر گام، دو خوشه‌ای با یکدیگر ادغام می‌شوند که دارای نزدیک‌ترین زوج از عناصر باشند، به شرطی که آن دو عنصر هنوز به یک خوشه تعلق نداشته باشند. در این حالت، فاصله بین دو گروه $ C_i $و $ C_j $برابر است با فاصله بین نزدیک‌ترین اعضای آن دو گروه:

\[d(C_i, C_j) = min[d(x_k, x_l)], x_k \in C_i, x_l \in C_j\]

این روش تمایل دارد خوشه‌هایی باریک و دراز تولید کند که در آن‌ها عناصر مجاورِ درون یک خوشه، فاصله‌ای اندک دارند، اما عناصر واقع در دو انتهای یک خوشه ممکن است فاصله‌ای بسیار بیشتر از دو عنصر متعلق به خوشه‌های دیگر از یکدیگر داشته باشند. برای برخی از داده ها، این ویژگی می‌تواند به ایجاد مشکلاتی در تعریف کلاس‌هایی که بتوانند داده را به شکلی درست تقسیم بندی کند، بینجامد. با این حال، این روش در اخترشناسی برای تحلیل خوشه‌های کهکشانی - که اغلب ممکن است شامل رشته‌های درازی از ماده باشند - پرطرفدار است. در این حوزه کاربردی، این الگوریتم با نام الگوریتم دوستانِ دوستان (friends-of-friends) نیز شناخته می‌شود.

Dendrogram

متد اتصال مجرد – مثال

فرض کنید ماتریس فاصله به روش اقلیدس برای 6 نقطه بصورت زیر است:

\[\begin{array}{c|ccccc} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 0 & 4 & 13 & 24 & 12 & 8 \\ 2 & & 0 & 10 & 22 & 11 & 10 \\ 3 & & & 0 & 7 & 3 & 9 \\ 4 & & & & 0 & 6 & 18 \\ 5 & & & & & 0 & 8.5 \\ 6 & & & & & & 0 \end{array}\]

حال قرار است که با توجه به فرمول اتصال مجرد، داده‌هایی که کمترین فاصله با یکدیگر را دارند، تشکیل یک خوشه بدهند. در این مثال، گروه جدید بین داده‌های 3 و 5 ساخته می‌شود؛ زیرا مقدار فاصله برای این دو داده مقدار کمینه (عدد 3) می‌باشد:

\[\begin{array}{c|ccccc} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 0 & 4 & 13 & 24 & 12 & 8 \\ 2 & & 0 & 10 & 22 & 11 & 10 \\ 3 & & & 0 & 7 & \textcircled{3} & 9 \\ 4 & & & & 0 & 6 & 18 \\ 5 & & & & & 0 & 8.5 \\ 6 & & & & & & 0 \end{array}\]

در این مرحله، فاصله‌ها بین گروه جدید و سایر گروه‌ها به شکل زیر محاسبه می‌شود:

( d_{1,(3,5)} = \min{d_{13}, d_{15}} = 12 ) ( d_{2,(3,5)} = \min{d_{23}, d_{25}} = 10 ) ( d_{4,(3,5)} = \min{d_{43}, d_{45}} = 6 ) ( d_{6,(3,5)} = \min{d_{63}, d_{65}} = 8.5 )

در این مرحله، با استفاده از ماتریس جدید تولید شده، مجدد مراحل را تکرار میکنیم:

\[\begin{array}{c|ccccc} & 1 & 2 & (3,5) & 4 & 6 \\ \hline 1 & 0 & \textcircled{4} & 12 & 24 & 8 \\ 2 & & 0 & 10 & 22 & 10 \\ (3,5) & & & 0 & 6 & 8.5 \\ 4 & & & & 0 & 18 \\ 6 & & & & & 0 \end{array}\]

که تشکیل چهار کلاس (1 و 2)، (3 و 5)، 4 و 6 میدهند:

( d_{(1,2) ,(3,5)} = \min{d_{13}, d_{23}, d_{15}, d_{25}} = 10 ) ( d_{(1,2) ,4} = \min{d_{14}, d_{24}} = 22 )

در مرحله بعد، ماتریس فاصله جدید به شکل زیر در خواهد آمد:

\[\begin{array}{c|ccccc} & (1,2) & (3,5) & 4 & 6 \\ \hline (1,2) & 0 & 10 & 22 & 8 \\ (3,5) & & 0 & \enclose{circle}{6} & 8.5 \\ 4 & & & 0 & 18 \\ 6 & & & & 0 \end{array}\]

ادامه میدهیم:

\[\begin{array}{c|ccccc} & (1,2) & (3,4,5) & 6 \\ \hline (1,2) & 0 & 10 & \enclose{circle}{8} \\ (3,4,5) & & 0 & 8.5 \\ 6 & & & 0 \end{array}\]

و در آخرین مرحله خواهیم داشت:

\[\begin{array}{c|ccccc} & (1,2,6) & (3,4,5) \\ \hline (1,2,6) & 0 & \enclose{circle}{8.5} \\ (3,4,5) & & 0 \\ \end{array}\]

دندروگرام این داده‌ها به شکل زیر خواهد بود:

Dendrogram

الگوریتم تجمعی پیشین در روش اتصال مجرد (single-link) نشان می‌دهد که برای اتصال دو گروه مجزا، تنها وجود یک پیوند کافی است. در این روش، فاصله‌ی میان دو گروه برابر است با فاصله‌ی نزدیک‌ترین اعضای آن‌ها. به همین دلیل، این روش را روش نزدیک‌ترین همسایگان نیز می‌نامند.

الگوریتم‌های تجمعی بر پایه تئوری ماتریس – متد اتصال کامل (Complete Link Method)

این روش هم بسیار شبیه به متد قبل است با این تفاوت که در این روش، معیار اتصال نقاط به شکل زیر تعریف می‌شود:

\[d(C_q, C_s) = max[d(C_i, C_s), d(C_j, C_s)]\]

این روش همچنین با نام روش دورترین همسایگان نیز شناخته می‌شود. در این روش، فاصله‌ی بین دو گروه $ C_i $ و $ C_j $ برابر است با فاصله‌ی بین دورترین نقاط به طوری که هر نقطه از یکی از دو گروه انتخاب می‌شوند:

\[d(C_i, C_j) = max[d(x_k, x_l)], x_k \in C_i, x_l \in C_j\]

توجه به این نکته حائز اهمیت است که در ترسیم نمودار دندروگرام در روش اتصال مجرد، خوشه‌های باریک و بلند ایجاد می‌شوند در حالیکه در روش اتصال کامل، خوشه‌ها بصورت فشرده و واضحتر رسم خواهند شد.

پیاده سازی به زبان پایتون

حال میخواهیم مثال بالا را با استفاده از پایتون پیاده سازی کرده و بصری سازی را انجام دهیم. پیش از انجام کامل این کار، ابتدا تمامی کتابخانه‌ها و توابعی که مورد نیاز است بطور جداگانه بررسی می‌شوند و سپس به پیاده‌سازی مثالها خواهیم رسید.

تابع pdist

تابع pdist یکی از ابزارهای پایه‌ای و بسیار مهم در خوشه‌بندی و تحلیل فاصله‌ها در پایتون است که در کتابخانه SciPy پیاده‌سازی شده است. این تابع در scipy.spatial.distance قرار دارد و مخفف pairwise distance (به معنی فاصله‌های دوتایی) می‌باشد. در این تابع، میتوان پارامتر metric را بنا بر متد محاسبه فاصله مورد نیاز (مانند اقلیدس و …) تنظیم کرد.

import numpy as np
from scipy.spatial.distance import pdist

X = np.array([
    [0, 0],
    [1, 2],
])
Y = pdist(X, metric='euclidean')

خروجی ماتریس Y، محاسبه فاصله دو نقطه (1, 1) و (0, 0) به روش اقلیدس است که به شکل زیر نمایش داده می‌شود:

array([2.23606798])

تابع linkage

تابع linkage مجددا از کتابخانه SciPy یکی از اصلیترین ابزارها برای اجرای خوشه‌بندی سلسله مراتبی تجمعی می‌باشد:

from scipy.cluster.hierarchy import linkage

این تابع، مراحل خوشه‌بندی را مرحله به مرحله انجام می‌دهد؛ یعنی از هر داده به عنوان یک خوشه شروع کرده و در هر مرحله، دو خوشه نزدیک به هم را با هم ادغام (merge) می‌کند تا در نهایت یک خوشه واحد بدست آید.

فرم کلی این تابع به شکل زیر است:

Z = linkage(y, method='single', metric='euclidean', optimal_ordering=False)

توضیحی راجع به پارامترهای این تابع در جدول زیر آورده شده است:

پارامتر	توضیح
`y`	داده‌ها (آرایه‌ی ویژگی‌ها یا فاصله‌ها)
`method`	روش ادغام خوشه‌ها
`metric`	نوع فاصله (در صورتی که `y` داده‌ی اصلی باشد)
`optimal_ordering`	در صورت True، ترتیب نمایش دندروگرام بهینه‌تر می‌شود

مثالی برای استفاده از این تابع در زیر ارائه شده است:

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

# داده‌ی نمونه
X = np.array([
    [1, 2],
    [2, 1],
    [3, 3],
    [6, 5],
    [7, 6]
])

# اجرای خوشه‌بندی
Z = linkage(X, method='single', metric='euclidean')

# نمایش خروجی Z
print(Z)

خروجی این کد به شکل زیر خواهد بود:

این تابع یک ماتریس به شکل $ 4 \times (1-n) $ برمیگرداندکه هر سطر آن، نشان دهنده یک مرحله ادغام است:

ستون	معنا
`Z[i,0]`	شماره‌ی خوشه‌ی اول ادغام‌شده
`Z[i,1]`	شماره‌ی خوشه‌ی دوم ادغام‌شده
`Z[i,2]`	فاصله‌ی بین این دو خوشه
`Z[i,3]`	تعداد نقاط در خوشه‌ی جدید پس از ادغام

یکی از اصلی‌ترین پارامترهای این تابع، method است که در موردی دو تا از آنها پیشتر صحبت شد. در جدول زیر، مجدد مروری بر موارد گفته شده داریم و باقی گزینه‌ها را معرفی می‌کنیم:

مقدار	توضیح
`'single'`	کمترین فاصله بین اعضای دو خوشه (single linkage)
`'complete'`	بیشترین فاصله بین اعضا
`'average'`	میانگین فاصله بین اعضا
`'ward'`	کمینه‌سازی واریانس داخل خوشه‌ها
`'centroid'`	فاصله بین مراکز خوشه‌ها
`'median'`	مشابه centroid ولی مقیاس متفاوت دارد

تابع dendrogram

همانطور که از اسم این تابع مشخص است، این تابع برای رسم نمودار دندروگرام استفاده می‌شود و همانند توابع قبلی، در کتابخانه SciPy تعریف شده است. این تابع در واقع یک دیکشنری برمیگرداند که حاوی اطلاعات رسم نمودار دندروگرام است.

from scipy.cluster.hierarchy import dendrogram

در قطعه کد پایین، مثالی از استفاده از این تابع آورده شده است:

from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

Z = linkage(X, method='single')
dendrogram(Z)
plt.show()

تابع inconsistent

شاید براتان سوال شده باشد که با کمک چه ابزاری می‌توان از درستی خوشه‌بندی تا حدی مطمئن شد. به جهت اطمینان نسبی از این روش، بحث Inconsistency مطرح می‌شود. ما به کمک این تابع، قدرت یا ضعف ادغام در خوشه‌ها در دندروگرام را بررسی می‌کنیم. بطور کلی فرمول محاسبه این مقدار به شکل زیر است:

\[inconsistancy = \frac{d - \mu}{\sigma}\]

که در آن:

$ d $: فاصله در گره فعلی (ادغام جاری)
$ \mu $: میانگین فاصله‌های ادغام‌های زیرین (فرزندان آن گره)
$ \sigma $: انحراف معیار فاصله‌های ادغام‌های زیرین

بنابراین اگر $ 𝑑 $ خیلی بزرگ‌تر از $ 𝜇 $، مقدار inconsistency بالا است.

در خوشه‌بندی سلسله مراتبی، هر مرحله از ادغام بین دو خوشه در ارتفاع خاصی انجام می‌شود. تابع inconsistent بررسی می‌کند که آیا این ادغام سازگار (consistent) است یا ناسازگار (inconsistent)؛ به این صورت که اگر ادغام فعلی خیلی بزرگتر از میانگین فاصله‌های ادغام‌های پایین‌تر باشد،ادغام “ناسازگار” است، یعنی احتمالا دو خوشه متفاوت با یکدیگر ترکیب شده‌اند.

تابع inconsistent هم به مانند توابع قبلی در کتابخانه SciPy تعریف شده است. فرم کلی استفاده از آن نیز در پایین آورده شده است:

from scipy.cluster.hierarchy import inconsistent

R = inconsistent(Z, depth=2)

توجه شود که Z همان خروجی تابع linkage است که پیشتر توضیح داده شد. پارامتر depth نیز بیان می‌کند که تا چه تعداد سطح پایین‌تری در محاسبه ناسازگاری لحاظ شود.

خروجی تابع inconsistent نیز شبیه به تابع linkage می‌باشد. این تابع یک آرایه $ 4 \times (1-n) $ برمیگرداند که هر سطح آن مرتبط با یک مرحله از ادغام است:

ستون	معنا
`R[i, 0]`	میانگین ارتفاع ادغام‌های زیرخوشه‌ها
`R[i, 1]`	انحراف معیار ارتفاع‌های زیرخوشه‌ها
`R[i, 2]`	تعداد ادغام‌هایی که برای محاسبه در نظر گرفته شدند
`R[i, 3]`	مقدار inconsistency فعلی: $ ((Z[i,2] - R[i,0]) / R[i,1]) $

حال بیایید به تفسیر مقادیر این معیار بپردازیم. ادغام سازگار یا ناسازگار را می‌توان از مقدار خروجی این تابع مشخص کرد که در جدول زیر بطور خلاصه توضیح داده شده است:

مقدار inconsistency	تفسیر
< 1.0	ادغام سازگار است (خوشه‌ها شبیه‌اند)
1.0 – 2.0	ادغام نسبتاً طبیعی است
> 2.0	ادغام ناسازگار است → احتمالاً خوشه‌های متفاوت با هم ترکیب شده‌اند

پس بطور کلی، با استفاده از تابع inconsistent می‌توان فهمید که کدام بخش از دندروگرام معنی‌دارتر است.

تابع fcluster

تابع fcluster استفاده می‌شود تا از روی نتیجه linkage، خوشه‌های نهایی را استخراج کند. به عبارت دیگر:

linkage فقط ساختار درختی را می‌سازد
ولی fcluster مشخص می‌کند که هر داده به کدام خوشه تعلق دارد.

from scipy.cluster.hierarchy import fcluster

clusters = fcluster(Z, t, criterion='distance')

توجه شود که Z همان خروجی تابع linkage است که پیشتر توضیح داده شد.

مقدار بازگشتی این تابع به صورت آرایه‌ای از شماره خوشه‌هاست (متناظر با هر داده در ورودی اولیه)؛ مثلا اگر 5 داده در دو خوشه داشته باشیم:

array([1, 1, 2, 2, 2])

تابع clusterdata

تابع clusterdata در واقع جمعبندی تمامی مواردی است که تا به الان گفته شد؛ یعنی:

pdist() ➜ linkage() ➜ fcluster

به این شکل که این تابع بصورت خودکار، تمامی مراحل خوشه‌بندی سلسله مراتبی را انجام می‌دهد؛ پس دیگر نیازی به محاسبه دستی فاصله‌ها و یا linkage نیست.

from scipy.cluster.hierarchy import clusterdata

clusterdata(X, method='single', metric='euclidean', t=1.0, criterion='inconsistent')

این تابع داده‌های ورودی را خوشه‌بندی می‌کند و خروجی‌اش شماره‌ی خوشه‌ی هر داده است.

نکته مهم: تابع clusterdata برای داده‌های کوچک و میان‌حجم عالی است، اما اگر داده‌های خیلی زیاد هستند یا کنترل دقیق‌تری روی مراحل خوشه‌بندی نیاز است، بهتر است از linkage() و fcluster() به‌صورت جداگانه استفاده شود.

حل یک مثال

کد زیر به جهت تفهیم بیشتر مفاهیم و یک مثال کامل آورده شده است. ابتدا کتابخانه‌ها و توابع مورد نیاز را به برنامه اضافه میکنیم:

import numpy as np
from scipy.spatial.distance import pdist, squareform
from scipy.cluster.hierarchy import linkage, dendrogram, inconsistent, fcluster
import matplotlib.pyplot as plt

حال با استفاده از تابع np.array()، دیتاهای خود را وارد برنامه می‌کنیم:

X = np.array([
    [2, 3],
    [4, 5],
    [7, 4],
    [2, 4],
    [3, 2],
    [8, 3]
])
print(X)

خروجی:

[[2 3]
 [4 5]
 [7 4]
 [2 4]
 [3 2]
 [8 3]]

با استفاده از تابع pdist() و متد اقلیدس، ماتریس تفاضل را ساخته و به کمک تابع squareform() آن را به شکل استاندارد (مربعی) نمایش می‌دهیم:

Y = pdist(X, 'euclidean')
print(squareform(Y))

خروجی:

[[0.         2.82842712 5.09901951 1.         1.41421356 6.        ]
 [2.82842712 0.         3.16227766 2.23606798 3.16227766 4.47213595]
 [5.09901951 3.16227766 0.         5.         4.47213595 1.41421356]
 [1.         2.23606798 5.         0.         2.23606798 6.08276253]
 [1.41421356 3.16227766 4.47213595 2.23606798 0.         5.09901951]
 [6.         4.47213595 1.41421356 6.08276253 5.09901951 0.        ]]

همانطور که از درسنامه بخاطر دارید، باید در این ماتریس به دنبال کمترین مقدار به جهت خوشه‌بندی بگردیم و آنها را با هم ادغام کنیم. مثلا در اولین قدم، داده اول و چهارم با کمترین مقدار فاصله (مقدار 1) با یکدیگر ادغام می‌شوند. با استفاده از تابع linkage()، این ادغام‌ها و فواصل بین خوشه‌ها را میتوان مشاهده کرد:

Z = linkage(Y, 'single', 'euclidean')
print(Z)

خروجی:

[[0.         3.         1.         2.        ]
 [4.         6.         1.41421356 3.        ]
 [2.         5.         1.41421356 2.        ]
 [1.         7.         2.23606798 4.        ]
 [8.         9.         3.16227766 6.        ]]

تفسیر خروجی تابع linkage() پیشتر آورده شده است. بطور مثال در سطر اول بیان شده که داده 0 و 3 با یکدیگر ادغام و میزان فاصله آنها از هم 1 بوده است. عدد آخر نشان میدهد که این خوشه در مجموع 2 داده دارد. به راحتی و با نوشتن تابع dendrogram میتوان نمودار آن را رسم کرد:

dendrogram(Z)

خروجی:

Dendrogram

R = inconsistent(Z, d=2)
print(W)

[[1.         0.         1.         0.        ]
 [1.20710678 0.29289322 2.         0.70710678]
 [1.41421356 0.         1.         0.        ]
 [1.82514077 0.58113883 2.         0.70710678]
 [2.27085307 0.87455104 3.         1.01929396]]

اما اگر بخواهیم این خروجی را تفسیر کنیم، همانطور که پیشتر گفته شد، نیاز است بدانیم کدام ستون چه مقادیری را برمیگردانند. بطور مثال، سطر دوم را بررسی می‌کنیم:

اولین عدد در این سطر متناظر با میانگین فاصله در خوشه است که مقدار آن 1.2 می‌باشد.
دومین مقدار نیز انحراف معیار را با مقدار 0.29 نشان می‌دهد.
مقدار سوم تعداد داده‌ها در هر خوشه است (2 داده)
و آخرین داده مربوط به ضریب ناسازگاریست که پیشتر توضیح آن داده شد (با مقدار 0.7)

میتوان خروجی این تابع را به ازای d=4 نیز بررسی کرد:

[[1.         0.         1.         0.        ]
 [1.20710678 0.29289322 2.         0.70710678]
 [1.41421356 0.         1.         0.        ]
 [1.55009385 0.62913719 3.         1.0903411 ]
 [1.84535455 0.86216774 5.         1.52745578]]

Inconsistancy

در نهایت با استفاده از fcluster، میتوانیم داده‌ها را در دسته‌های (خوشه‌ها)، دسته‌بندی کنیم:

T = fcluster(Z, 1, depth=2)
print(T)

خروجی:

[2 2 1 2 2 1]

پر واضخ است که داده‌ها در دو دسته و با برچسب 1 و 2 خوشه‌بندی شده‌اند؛ به این شکل که داده اول و دوم در خوشه 2 و داده سوم در خوشه 1 و … قرار گرفته‌اند.

تولید چرخ از اول!

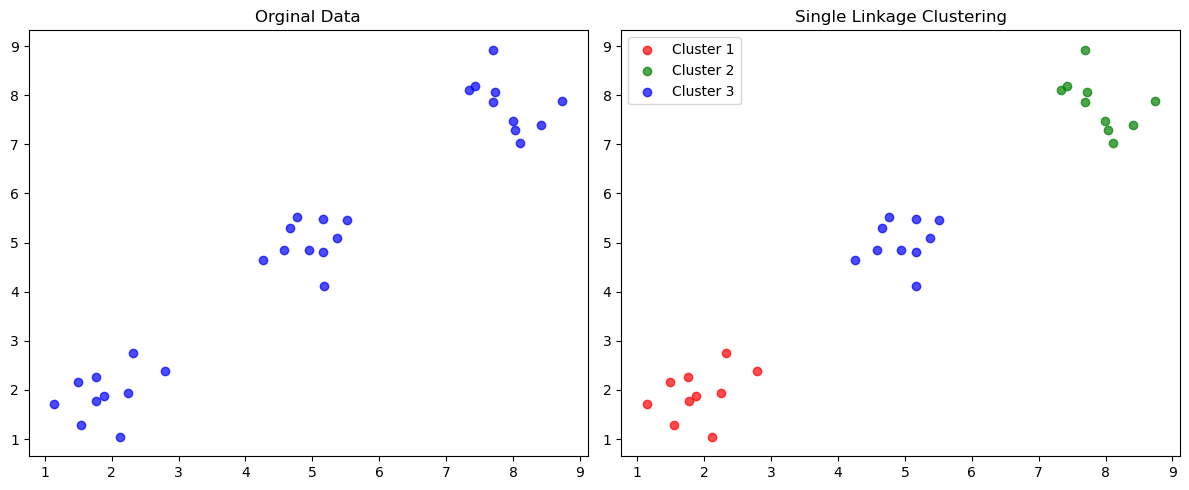
اگر شما هم جزو کسانی هستید که دوست دارن چرخ را از ابتدا و به دست خودشان تولید کنند، کد زیر پیاده سازی روش single-linkage clustring هست که دید بسیار خوبی به شما خواهد داد و به راحتی میتوان پارامتر های آن را جایگزین و تمامی تغییرات را بررسی کرد. قطعا برای انجام محاسبات دم دستی و سریع، استفاده از کتابخانه scipy بسیار راحت تر و سریعتر خواهد بود، اما اگر قصد تغییرات و یا اضافه کردن مواردی به این الگوریتم را دارید، نیاز است که خودتان دست بکار شده و تمامی مراحل را از ابتدا و با ایده های خودتان پیاده سازی کنید. قطعا به مدل های متفاوتی میتوان این الگوریتم را پیاده سازی و مصورسازی کرد که در ادامه، به آوردن یک نمونه از آن اکتفا میکنیم:

import numpy as np
from scipy.spatial.distance import pdist, squareform
import matplotlib.pyplot as plt

class SingleLinkageClustering:
    def __init__(self):
        self.labels_ = None
        self.distances_ = None
        
    def fit(self, X, n_clusters=2):
        """
        Single Linkage Clustering
        
        Parameters:
        X : array-like, shape (n_samples, n_features)
            Input data
        n_clusters : int, default=2
            Number of clusters to form
        """
        n_samples = X.shape[0]
        
        # محاسبه ماتریس فاصله
        self.distances_ = squareform(pdist(X))
        
        # مقداردهی اولیه: هر نقطه یک خوشه است
        clusters = [[i] for i in range(n_samples)]
        
        # الگوریتم سلسله مراتبی
        while len(clusters) > n_clusters:
            # پیدا کردن نزدیک‌ترین دو خوشه
            min_distance = float('inf')
            merge_i, merge_j = -1, -1
            
            for i in range(len(clusters)):
                for j in range(i + 1, len(clusters)):
                    # محاسبه فاصله single linkage (حداقل فاصله بین نقاط دو خوشه)
                    distance = self._single_linkage_distance(clusters[i], clusters[j])
                    if distance < min_distance:
                        min_distance = distance
                        merge_i, merge_j = i, j
            
            # ادغام دو خوشه
            clusters[merge_i].extend(clusters[merge_j])
            clusters.pop(merge_j)
        
        # ایجاد برچسب‌های خوشه
        self.labels_ = np.zeros(n_samples, dtype=int)
        for cluster_idx, cluster in enumerate(clusters):
            for point_idx in cluster:
                self.labels_[point_idx] = cluster_idx
                
        return self
    
    def _single_linkage_distance(self, cluster1, cluster2):
        """محاسبه فاصله single linkage بین دو خوشه"""
        min_distance = float('inf')
        for i in cluster1:
            for j in cluster2:
                distance = self.distances_[i, j]
                if distance < min_distance:
                    min_distance = distance
        return min_distance

# مثال استفاده
if __name__ == "__main__":
    # تولید داده‌های نمونه
    np.random.seed(42)
    
    # سه خوشه مجزا
    cluster1 = np.random.normal(2, 0.5, (10, 2))
    cluster2 = np.random.normal(8, 0.5, (10, 2))
    cluster3 = np.random.normal(5, 0.5, (10, 2))
    
    X = np.vstack([cluster1, cluster2, cluster3])
    
    # اجرای الگوریتم
    slc = SingleLinkageClustering()
    slc.fit(X, n_clusters=3)
    
    # نمایش نتایج
    plt.figure(figsize=(12, 5))
    
    plt.subplot(1, 2, 1)
    plt.scatter(X[:, 0], X[:, 1], c='blue', alpha=0.7)
    plt.title('Orginal Data')
    
    plt.subplot(1, 2, 2)
    colors = ['red', 'green', 'blue', 'orange', 'purple']
    for i in range(3):
        cluster_points = X[slc.labels_ == i]
        plt.scatter(cluster_points[:, 0], cluster_points[:, 1], 
                   c=colors[i], label=f'Cluster {i+1}', alpha=0.7)
    plt.title('Single Linkage Clustering')
    plt.legend()
    
    plt.tight_layout()
    plt.show()

در انتها، نمونه تصویری از خروجی کد بالا آورده شده است:

Single Linkage

روش های تجمیعی در یادگیری ماشین

Hadi Sadoghi Yazdi

روش‌های تجمعی (Agglomerative Methods) در یادگیری ماشین

مقدمه

تعریف تئوری ماتریس با یک مثال

دندروگرام (Dendrogram)

الگوریتم‌های تجمعی بر پایه تئوری ماتریس – متد اتصال مجرد (Single Link Method)

متد اتصال مجرد – مثال

الگوریتم‌های تجمعی بر پایه تئوری ماتریس – متد اتصال کامل (Complete Link Method)

پیاده سازی به زبان پایتون

تابع pdist

تابع linkage

تابع dendrogram

تابع inconsistent

تابع fcluster

تابع clusterdata

حل یک مثال

تولید چرخ از اول!

منابع