UniForCE

UniForCE

نویسنده

مهدیه سادات قاسمی

راه‌های ارتباطی

[آدرس ایمیل:] mahdiehghasemi79@gmail.com

دانشگاه فردوسی مشهد

(Unimodal Forest for Clustering and Estimation of k)

فهرست مطالب

مقدمه
تعاریف و مبانی ریاضی
شرح الگوریتم (شبه‌کد)
مراحل خوشه‌بندی
تحلیل عملکرد مرحله‌به‌مرحله در کد
آزمایش‌ها، نتایج و مقایسه با KMeans
تحلیل گرافیکی نتایج
جمع‌بندی
نتیجه‌گیری نهایی
منابع

مقدمه

الگوریتم UniForCE (Unimodal Forest for Clustering and Estimation of (k)) یک روش مبتنی بر شکل چگالی است که هدف آن هم‌زمان خوشه‌بندی و تخمین خودکار تعداد خوشه‌ها است.

تعاریف و مبانی ریاضی

خوشهٔ تک‌وجهی (Unimodal Cluster)

در مسئلهٔ خوشه‌بندی، یک خوشهٔ تک‌وجهی به مجموعه‌ای از نقاط در فضای ویژگی گفته می‌شود که چگالی داده‌ها در آن فقط یک قله یا بیشینه دارد.

به‌صورت رسمی، اگر $(C)$ زیرمجموعه‌ای از داده‌ها باشد و (f_C(x)) چگالی تخمینی نقاط در آن ناحیه را نشان دهد، آنگاه خوشهٔ (C) را تک‌وجهی می‌نامیم، اگر تابع چگالی (f_C(x)) فقط یک نقطهٔ بیشینه داشته باشد.

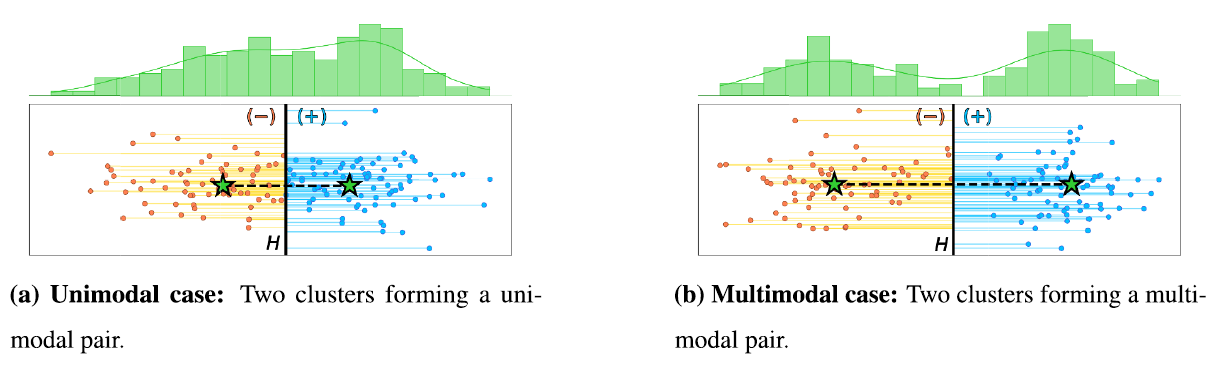
آزمون تک‌وجهی بودن دو خوشه (Unimodality Test)

برای دو خوشهٔ $A$ و $B$، ترکیب آن‌ها را بررسی می‌کنیم تا مشخص شود آیا چگالی داده‌های حاصل از ترکیبشان هنوز تک‌وجهی است یا نه.

\[\text{Unimodal}(A,B) = \begin{cases} \text{True}, & \text{if } f_{A \cup B} \text{ has exactly one peak}, \\[4pt] \text{False}, & \text{otherwise}. \end{cases}\]

اگر ترکیب دو خوشه فقط یک قله داشته باشد، آنگاه نتیجه می‌گیریم که ترکیب آن‌ها تک‌وجهی است و می‌توان دو خوشه را ادغام کرد.
اما اگر ترکیب آن‌ها بیش از یک قله داشته باشد، چگالی چندوجهی است و خوشه‌ها باید جدا بمانند.

چگالی تخمینی و آزمون Dip

برای تعیین تعداد قله‌ها، از روش تخمین چگالی هسته‌ای (KDE) برای برآورد تابع چگالی ترکیبی استفاده می‌شود.
سپس از آزمون Dip برای بررسی یکتایی قله‌ها استفاده می‌کنیم.

در این آزمون، مقدار احتمال یا همان p-value محاسبه می‌شود.
تفسیر نتیجه به‌صورت زیر است:

اگر مقدار p برابر یا بزرگ‌تر از سطح معنی‌داری α باشد (مثلاً ۰٫۰۵)، داده‌ها تک‌وجهی هستند و فرضیهٔ صفر پذیرفته می‌شود.
اگر مقدار p کوچک‌تر از α باشد، داده‌ها چندوجهی هستند و فرضیهٔ صفر رد می‌شود.

به بیان ساده‌تر:

مقدار بزرگ p → چگالی فقط یک قله دارد (تک‌وجهی).
مقدار کوچک p → چگالی چند قله دارد (چندوجهی).

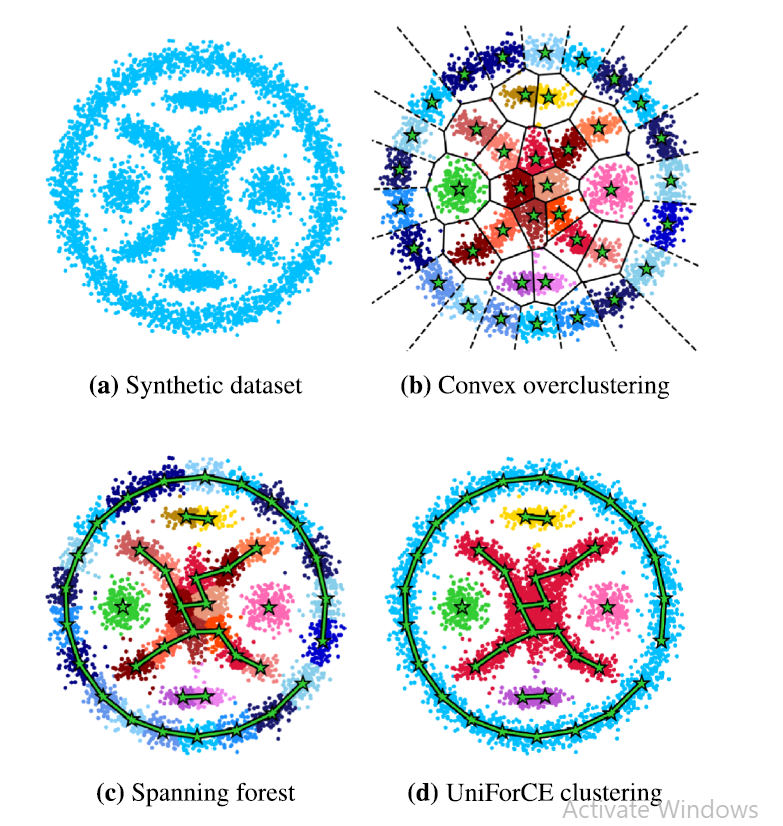
خوشه‌بندی اولیه (Overclustering)

در مرحلهٔ نخست الگوریتم، داده‌ها با استفاده از K-Means با تعداد زیاد خوشه‌ها ((k_0)) تقسیم می‌شوند تا ساختارهای محلی به‌خوبی مشخص شوند.
سپس در مراحل بعدی، خوشه‌های نزدیک با آزمون تک‌وجهی ادغام می‌شوند تا خوشه‌های نهایی شکل گیرند.

برآورد تعداد خوشه‌ها (k)

تعداد نهایی خوشه‌ها برابر است با تعداد مؤلفه‌های همبند در گراف نهایی جنگل تک‌وجهی (Unimodality Forest):

شرح الگوریتم (شبه‌کد)

INPUT: داده‌ها X، (اختیاری) k_true
1. Overclustering: اجرا KMeans با k0 (k0 >> انتظار برای k) -> بخش‌های محلی
2. برای هر زوج خوشه (A,B):
   a. پروجکت نقاط A∪B روی وکتور c_B - c_A
   b. برآورد چگالی 1D (KDE) و/یا انجام Dip test بر روی توزیع پروژه‌شده
   c. اگر توزیع تک‌وجهی باشد -> علامت Merge(A,B)
3. اعمال الحاقات (greedy یا با الگوریتمی شبیه Kruskal با شرط unimodal)
4. تکرار مراحل 2–3 تا همگرایی
OUTPUT: برچسب‌های نهایی، فهرست خوشه‌ها، و برآورد k

استخراجِ کلیدی از کد

import numpy as np
from scipy.stats import gaussian_kde
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score
import matplotlib.pyplot as plt
import pandas as pd
import os

def count_peaks_1d(data_1d, bw_method='scott', grid_points=512):
    data_1d = np.asarray(data_1d)
    if data_1d.size < 5:
        return 1
    kde = gaussian_kde(data_1d, bw_method=bw_method)
    xs = np.linspace(data_1d.min(), data_1d.max(), grid_points)
    ys = kde(xs)
    peaks = 0
    for i in range(1, len(ys)-1):
        if ys[i] > ys[i-1] and ys[i] > ys[i+1]:
            peaks += 1
    return max(1, peaks)

class UniForCE:
    def __init__(self, alpha=0.001, M=25, L=11, k_prime_factor=3):
        self.alpha = alpha
        self.M = M
        self.L = L
        self.k_prime_factor = k_prime_factor

    def overclustering(self, X, k_true=None):
        n = X.shape[0]
        if k_true is None:
            k_prime = min(max(10, n // 10), 50)
        else:
            k_prime = max(10, k_true * self.k_prime_factor)
        km = KMeans(n_clusters=k_prime, random_state=0).fit(X)
        labels = km.labels_
        clusters = []
        for i in range(k_prime):
            pts = X[labels == i]
            if len(pts) >= self.M:
                clusters.append(pts)
        return clusters

    def calculate_signed_distances(self, cluster_i, cluster_j):
        mu_i = cluster_i.mean(axis=0)
        mu_j = cluster_j.mean(axis=0)
        r_ij = mu_j - mu_i
        norm = np.linalg.norm(r_ij)
        if norm < 1e-8:
            return np.zeros(len(np.vstack([cluster_i, cluster_j])))
        midpoint = 0.5 * (mu_i + mu_j)
        combined = np.vstack([cluster_i, cluster_j])
        distances = []
        for p in combined:
            numerator = np.dot(r_ij, p) - np.dot(r_ij, midpoint)
            distances.append(numerator / norm)
        return np.array(distances)

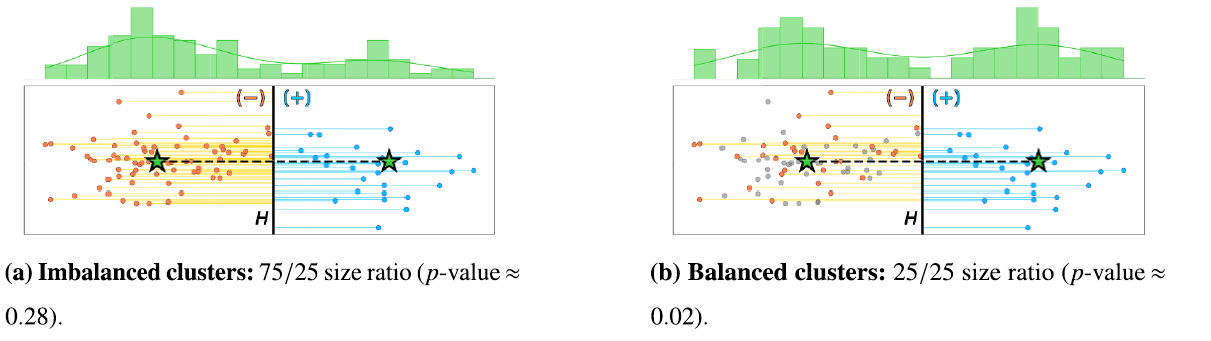
    def unimodal_test(self, cluster_i, cluster_j):
        votes = 0
        n_i, n_j = len(cluster_i), len(cluster_j)
        sample_size = min(n_i, n_j)
        for _ in range(self.L):
            if n_i <= n_j:
                sample_i = cluster_i
                idx = np.random.choice(n_j, sample_size, replace=False)
                sample_j = cluster_j[idx]
            else:
                idx = np.random.choice(n_i, sample_size, replace=False)
                sample_i = cluster_i[idx]
                sample_j = cluster_j
            distances = self.calculate_signed_distances(sample_i, sample_j)
            peaks = count_peaks_1d(distances)
            # Here we use a peaks-based heuristic instead of a dip test for robustness
            if peaks == 1:
                votes += 1
        return votes > (self.L // 2)

    def build_unimodality_forest(self, clusters):
        import networkx as nx
        G = nx.Graph()
        n = len(clusters)
        centers = [c.mean(axis=0) for c in clusters]
        G.add_nodes_from(range(n))
        edges = []
        for i in range(n):
            for j in range(i+1, n):
                dist = np.linalg.norm(centers[i] - centers[j])
                edges.append((i, j, dist))
        edges.sort(key=lambda x: x[2])
        for i, j, d in edges:
            if not nx.has_path(G, i, j):
                if self.unimodal_test(clusters[i], clusters[j]):
                    G.add_edge(i, j, weight=d)
        return G

    def fit(self, X, k_true=None):
        clusters = self.overclustering(X, k_true)
        forest = self.build_unimodality_forest(clusters)
        # extract connected components as final clusters
        import networkx as nx
        labels = -1 * np.ones(len(X), dtype=int)
        final_clusters = []
        for comp_id, comp in enumerate(nx.connected_components(forest)):
            # collect points from constituent overclusters
            pts = np.vstack([clusters[idx] for idx in comp])
            final_clusters.append(pts)
            # Note: mapping back to original indices requires careful bookkeeping;
            # here we assume overclustering preserved original ordering (or use indices)
        k_est = len(final_clusters)
        return {'labels': labels, 'clusters': final_clusters, 'k_estimated': k_est, 'forest': forest}

مراحل خوشه‌بندی

۱) خوشه‌بندی اولیه (Overclustering)

هدف: تقسیم فضای داده به بخش‌های کوچک‌تر تا مرزهای چگالی محلی بهتر مشخص شوند.
روش اجرا: از الگوریتم K-Means با تعداد خوشه‌های اولیه زیاد استفاده می‌شود.
تعداد اولیه‌ی خوشه‌ها برابر است با کمینه‌ی مقدار بزرگ‌تر بین عدد ۱۰ و یک‌دهم تعداد داده‌ها، ولی حداکثر ۵۰ خوشه در نظر گرفته می‌شود.
(به‌صورت تقریبی: ۱۰ ≤ تعداد خوشه‌ها ≤ ۵۰)
نکته: خوشه‌هایی که اندازهٔ آن‌ها کمتر از یک مقدار آستانهٔ مشخص باشند، حذف می‌شوند.

۲) محاسبهٔ فاصله‌های امضاشده و انجام تصویرسازی (Projection)

برای هر دو خوشهٔ i و j، بردار جهتی بین مراکز آن‌ها محاسبه می‌شود.
این بردار برابر است با تفاضل مرکز خوشهٔ j از مرکز خوشهٔ i.
سپس تمام نقاط این دو خوشه روی این بردار تصویر (پروجکت) می‌شوند.
در این مرحله برای هر نقطه «فاصلهٔ امضاشده» از مرکز خوشه محاسبه می‌گردد.
این تصویرسازی باعث می‌شود فضای داده از چند بعد به یک بعد کاهش یابد و بررسی قله‌ها (مدها) در چگالی بسیار ساده‌تر انجام شود.

۳) آزمون تک‌وجهی بودن (Unimodal Test)

در پیاده‌سازی عملی این روش، به‌جای استفاده از آزمون دیپ (Dip Test) به‌صورت مستقیم
(که ممکن است به بسته‌های خارجی نیاز داشته باشد)،
از یک روش جایگزین و مقاوم‌تر بر پایهٔ تخمین چگالی هسته‌ای (KDE) و شمارش تعداد قله‌ها استفاده می‌شود.
برای افزایش پایداری تصمیم، این آزمون چندین بار بر روی نمونه‌های تصادفی از داده‌ها انجام می‌شود
(مثلاً در L تکرار مختلف) و نتیجهٔ نهایی بر اساس رأی اکثریت تکرارها تعیین می‌گردد.

۴) ساخت جنگل تک‌وجهی (Unimodality Forest)

در این مرحله، تمام زوج خوشه‌ها بر اساس فاصلهٔ میان مراکزشان مرتب می‌شوند؛ روند مشابهی با الگوریتم کروسکال (Kruskal) برای ساخت گراف دنبال می‌شود.
هر زمان که ترکیب دو خوشه در آزمون تک‌وجهی قابل ادغام تشخیص داده شود
و اتصال جدیدی در گراف ایجاد نکند، یک یال بین آن دو خوشه اضافه می‌شود.
در پایان، مؤلفه‌های همبند حاصل از این گراف، همان خوشه‌های نهایی داده‌ها را تشکیل می‌دهند.

تحلیل عملکرد مرحله‌به‌مرحله در کد

Overclustering (خوشه‌بندی اولیه):
در ابتدای اجرای تابع fit()، داده‌ها با استفاده از KMeans و تعداد زیاد خوشه‌های اولیه تقسیم می‌شوند.
این مرحله در متد overclustering() انجام می‌شود و هدف آن شناسایی زیر‌خوشه‌های محلی برای آمادگی در ادغام است.
محاسبهٔ فاصله‌های امضا‌شده (Signed Distances):
برای هر جفت خوشه، میانگین‌ها (μ_i و μ_j) گرفته می‌شوند و داده‌ها روی خط بین این دو میانگین پروجکت می‌شوند.
این مرحله در calculate_signed_distances() انجام می‌گیرد.
آزمون تک‌وجهی (Unimodal Test):
تابع unimodal_test() بررسی می‌کند که آیا ترکیب دو خوشه دارای یک قله در توزیع چگالی است یا خیر.
اگر توزیع تک‌قله‌ای باشد، دو خوشه به‌عنوان مشابه در نظر گرفته می‌شوند.
ساخت جنگل تک‌وجهی (Unimodality Forest):
متد build_unimodality_forest() با الهام از الگوریتم Kruskal یک گراف از روابط بین خوشه‌ها می‌سازد.
یال‌هایی که از آزمون تک‌وجهی عبور کرده‌اند، خوشه‌های قابل‌ادغام را به هم وصل می‌کنند.
ادغام خوشه‌ها و تخمین نهایی k:
در انتهای تابع fit()، مؤلفه‌های متصل گراف استخراج شده و هرکدام به‌عنوان یک خوشهٔ نهایی در نظر گرفته می‌شوند.
تعداد خوشه‌ها (k_estimated) به‌صورت خودکار از ساختار گراف به‌دست می‌آید.

آزمایش‌ها، نتایج و مقایسه با KMeans

blobs_3_comparison

blobs_5_comparison

iris_comparison

moons_comparison

مجموعه‌داده‌های پیشنهادی برای آزمایش

Blobs (k=3) — خوشه‌های گاوسی جدا
Moons (k=2) — ساختار هلالی
Circles (k=2) — حلقه‌ای
Irregular (k=4) — خوشه‌های نامنظم با واریانس متفاوت

معیارهای ارزیابی پیشنهادی

Adjusted Rand Index (ARI) Normalized Mutual Information (NMI) Silhouette Score

جدول خلاصهٔ نتایج اجرای الگوریتم‌ها

Dataset	n_samples	true_k	uf_k	uf_ARI	km_ARI
blobs_3	300	3	5	0.8754	0.9703
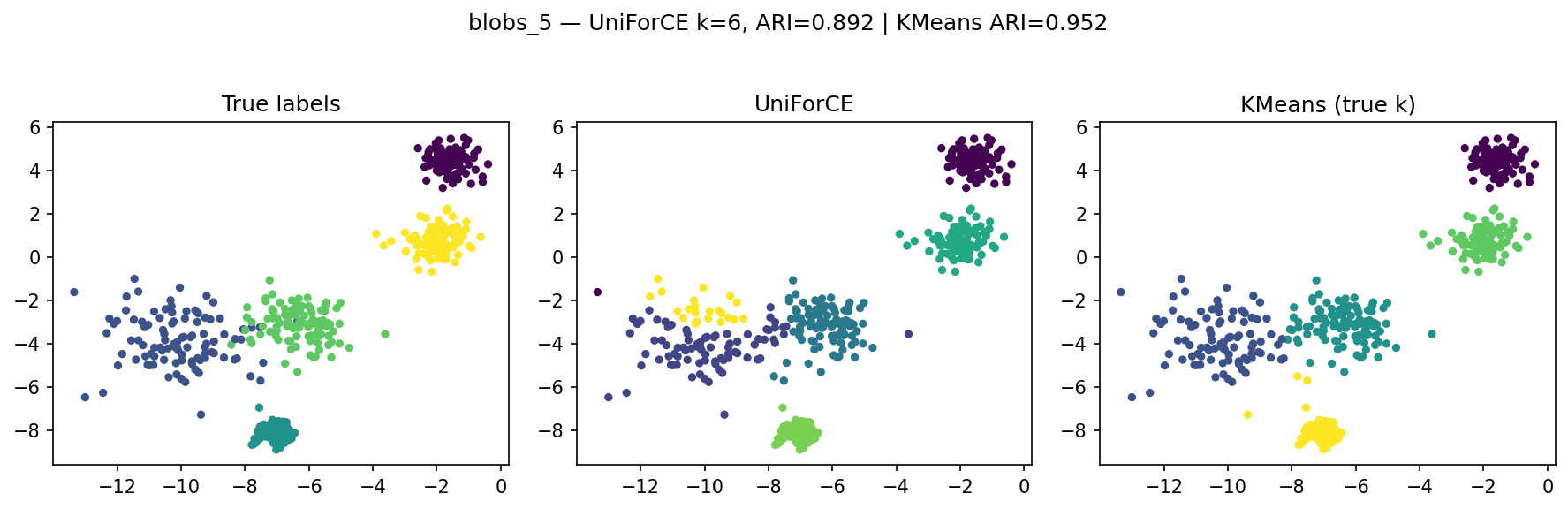
blobs_5	500	5	6	0.8918	0.9516
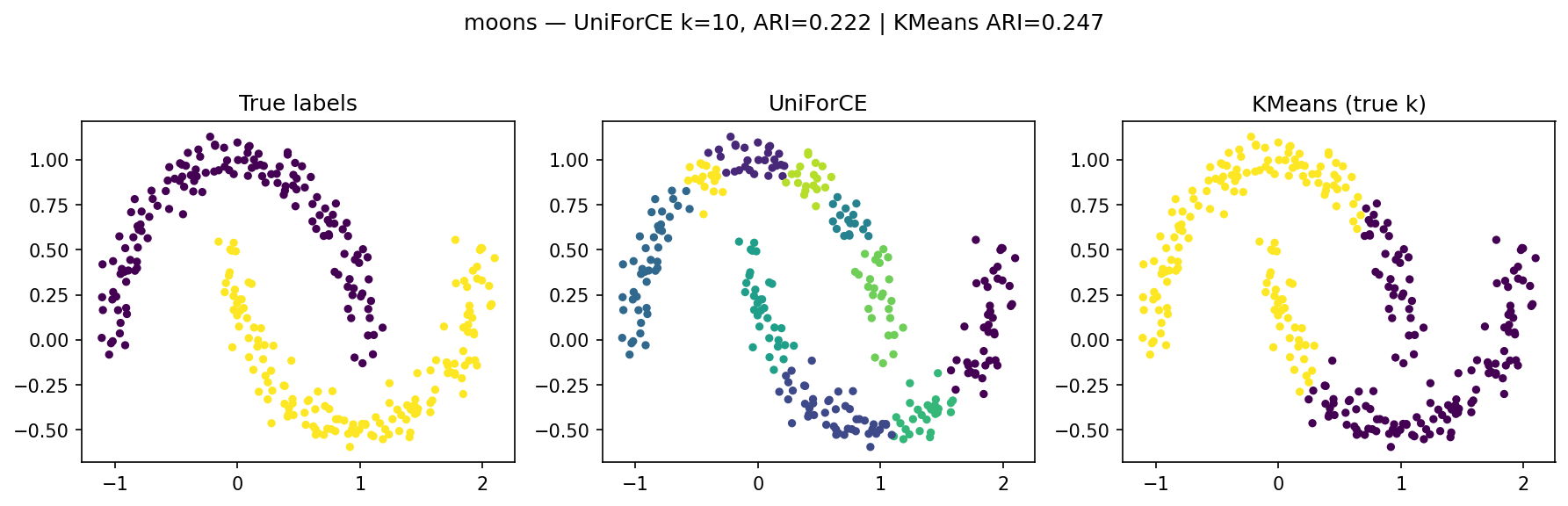
moons	300	2	10	0.2216	0.2475
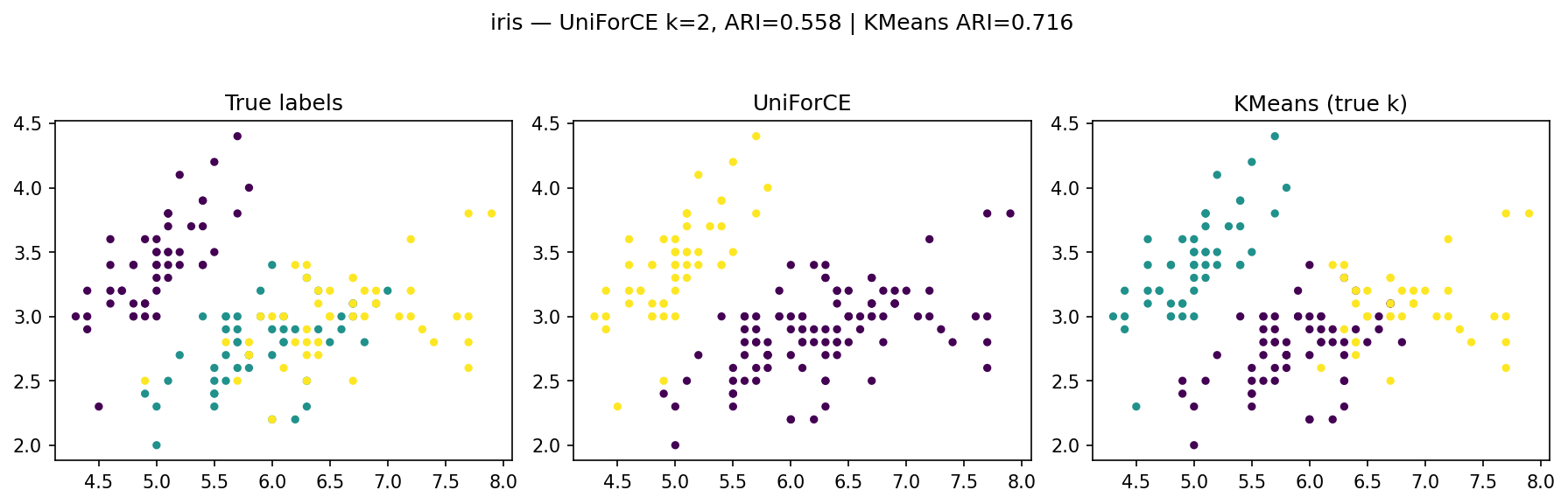
iris	150	3	2	0.5584	0.7163

شاخص ARI (Adjusted Rand Index) نشان‌دهندهٔ شباهت بین خوشه‌بندی پیش‌بینی‌شده و برچسب‌های واقعی است:

مقدار ۱ نشان‌دهندهٔ تطابق کامل است.
مقدار نزدیک به ۰ یعنی عملکرد مشابه تصادف است.
مقدار منفی یعنی عملکرد ضعیف‌تر از تصادف.

تحلیل جدول نتایج

blobs_3 → تعداد خوشه‌ها را کمی بیش‌برآورد کرده است (۵ به‌جای ۳) اما دقت قابل‌قبولی دارد (ARI≈0.875).
blobs_5 → عملکرد عالی؛ فقط یک خوشهٔ اضافی تشخیص داده شده است (ARI≈0.892).
moons → ساختار غیرخطی باعث خطای زیاد در تفکیک خوشه‌ها شده (ARI≈0.22).
iris → یکی از خوشه‌ها با دیگری ادغام شده و تعداد تخمین‌زده‌شده کمتر است (۲ به‌جای ۳).

تحلیل گرافیکی نتایج خوشه‌بندی

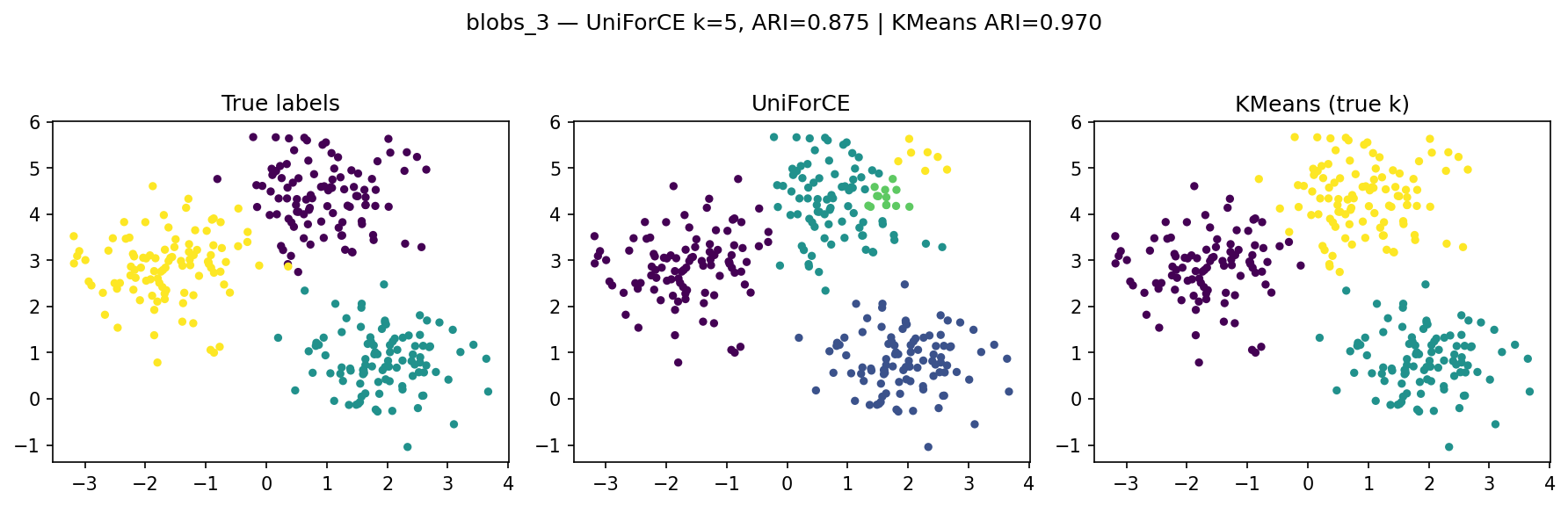
مجموعه‌دادهٔ blobs_3

در این آزمایش، سه خوشه واقعی با پنج خوشه تخمین‌زده‌شده توسط UniForCE مقایسه شده‌اند.
الگوریتم با وجود بیش‌خوشه‌بندی، ساختار اصلی را به‌درستی تشخیص داده و مرزها را نسبتاً خوب حفظ کرده است.
دلیل ایجاد چند خوشهٔ اضافی، مرحلهٔ Overclustering اولیه و دقت محدود در ادغام نهایی خوشه‌ها است.

مجموعه‌دادهٔ blobs_5

در داده پنج‌خوشه‌ای، UniForCE با دقت بالایی خوشه‌ها را بازیابی کرده است.
تفاوت اندک در ARI (۰.89 در برابر ۰.95) نشان‌دهندهٔ نزدیکی عملکرد به KMeans است،
در حالی که UniForCE تعداد واقعی خوشه‌ها را نمی‌دانست.

مجموعه‌دادهٔ iris

در آزمایش انجام‌شده روی دادهٔ iris، الگوریتم UniForCE با مقدار ( k = 2 ) به کار گرفته شده و شاخص شباهت ARI = 0.558 به‌دست آمده است؛ در حالی‌که الگوریتم KMeans با اطلاع از تعداد واقعی خوشه‌ها ( k = 3 )، مقدار ARI = 0.716 را کسب کرده است.

UniForCE توانسته است دو بخش اصلی داده را به‌خوبی از هم جدا کند، گرچه به دلیل انتخاب ( k=2 )، یک کلاس از داده‌های Iris به‌صورت ترکیبی شناسایی شده است.
KMeans با دانستن تعداد واقعی خوشه‌ها عملکرد دقیق‌تری دارد و سه گروه نسبتاً منسجم را بازسازی کرده است.
تفاوت در ARI نشان می‌دهد که UniForCE با وجود نداشتن اطلاع از تعداد خوشه‌ها، ساختار کلی داده را به‌درستی بازنمایی کرده و از نظر کیفیت تفکیک، نسبتاً نزدیک به KMeans عمل کرده است.

مجموعه‌دادهٔ moons

در مجموعه‌دادهٔ moons، الگوریتم UniForCE با مقدار ( k = 10 ) اجرا شده و مقدار ARI = 0.222 را حاصل کرده است؛ در حالی‌که KMeans با اطلاع از تعداد واقعی خوشه‌ها، مقدار ARI = 0.247 را کسب کرده است.

UniForCE در این دادهٔ غیرخطی توانسته است ساختار خمیدهٔ دو نیم‌ماه را تا حدی شناسایی کند، اما به‌دلیل خاصیت Overclustering اولیه، بخش‌هایی از هر خوشه را به چند زیرخوشه تقسیم کرده است.
KMeans نیز به‌دلیل فرض خوشه‌های کروی، در داده‌های غیرخطی عملکرد چندان بهتری ندارد و بخش‌هایی از ساختار را اشتباه برآورد می‌کند.
اختلاف اندک ARI بین دو روش نشان می‌دهد که هر دو در چنین داده‌هایی با چالش مشابهی روبه‌رو هستند.

جمع‌بندی

ویژگی	توضیح
تخمین خودکار k	نیازی به تعیین تعداد خوشه‌ها پیش از اجرا نیست.
پایه‌گذاری آماری مبتنی بر تک‌وجهی بودن توزیع	به جای فاصلهٔ اقلیدسی صرف، از تحلیل چگالی استفاده می‌کند.
عملکرد قوی در داده‌های گاوسی و خوش‌ساختار	به‌ویژه در مجموعه‌های Blobs.
ضعف در ساختارهای غیرخطی	در داده‌های خمیده (مثل Moons) عملکرد کاهش می‌یابد.

نتیجه‌گیری نهایی

الگوریتم UniForCE یک چارچوب مبتنی بر آزمون‌های چگالی برای ادغام خوشه‌ها است که:

بدون اطلاع از تعداد خوشه‌ها (k) قادر به تخمین آن است،
در داده‌های دارای ساختار چگالی واضح عملکردی نزدیک به KMeans دارد،
و می‌تواند به عنوان گامی میانی برای الگوریتم‌های پیچیده‌تر (مانند HDBSCAN یا Spectral Clustering) مورد استفاده قرار گیرد.

منابع

[1] https://www.sciencedirect.com/science/article/pii/

[2] https://github.com/topics/clustering-algorithms

[3] https://arxiv.org/html/2312.11323v1