استخراج ویژگی از تصاویر و خوشه بندی
مقدمه و تعریف مسئله
در این پروژه، به بررسی و پیادهسازی روشهای مختلف خوشهبندی تصاویر با استفاده از ویژگی های استخراج شده ازشبکه های عصبی عمیق میپردازیم. هدف اصلی این است که تصاویر را بر اساس محتوای بصریشان به گروههای معنادار تقسیم کنیم. برای این منظور، ابتدا از شبکه عصبی پیشآموزشدیده VGG16 برای استخراج ویژگیهای تصاویر استفاده میکنیم. سپس با بکارگیری توابع ضرر مختلف (از جمله L1، L2، Huber، Correntropy و …) و تکنیکهای بهینهسازی عددی، خوشهبندی را انجام میدهیم.
سپس برای درک بهتر از نتایج مرکز خوشه ها که نشان دهنده تصاویر موجود در داده های ما هستند را نمایش می دهیم. این تصاویر (مراکز خوشه) نقاطی در فضای ویژگی های ما هستند که کمترین مجموع فاصله را با سایر نقاط دارند.
این پروژه نشان میدهد که انتخاب تابع ضرر مناسب چگونه میتواند بر نتایج خوشهبندی تأثیر بگذارد. همچنین تفاوت بین روشهای تحلیلی و بهینهسازی عددی را برای یافتن مراکز بهینه خوشهها بررسی میکنیم.
یادگیری بدون نظارت و خوشهبندی
یادگیری بدون نظارت به تکنیکهایی اطلاق میشود که بدون نیاز به دادههای برچسبدار، الگوها و گروهبندیها را در دادهها کشف میکنند. خوشهبندی یکی از رایجترین روشهای یادگیری بدون نظارت است که دادهها را به گروههایی (خوشهها) تقسیم میکند به گونهای که عناصر درون هر خوشه شباهت بیشتری به یکدیگر نسبت به عناصر خوشههای دیگر داشته باشند. با اعمال خوشهبندی بر روی ویژگیهای استخراجشده از تصاویر، میتوانیم به طور خودکار تصاویر را بر اساس محتوای بصریشان به گروههای معناداری سازماندهی کنیم.
این پروژه الگوریتمهای خوشهبندی تعمیمیافته را با استفاده از توابع ضرر مختلف پیادهسازی میکند که امکان گروهبندی انعطافپذیر و مقاوم تصاویر را فراهم میآورد. نتایج بهدستآمده بینشی درباره ساختار مجموعه داده تصویری ارائه میدهد و قدرت ترکیب استخراج ویژگی عمیق با یادگیری بدون نظارت را نشان میدهد.
اهمیت استخراج ویژگی
تصاویر به طور کلی دادههایی با ابعاد بالا هستند که معمولاً شامل هزاران یا میلیونها پیکسل میباشند. استفادهی مستقیم از این مقادیر پیکسل برای وظایف یادگیری ماشین، ناکارآمد و بهندرت مؤثر است، زیرا این مقادیر الگوها یا محتوای معنایی زیرین تصویر را بهخوبی نمایش نمیدهند. استخراج ویژگی، تصاویر خام را به نمایشهای فشرده و آگاهانهای تبدیل میکند که اطلاعات بصری اساسی را خلاصه میسازند. این کار باعث میشود وظایف بعدی مانند طبقهبندی، خوشهبندی و بازیابی، مقاومتر و از نظر محاسباتی امکانپذیرتر شوند.
شبکه های عصبی CNN و مدل VGG16
شبکههای عصبی کانولوشنی یا به اختصار (CNN) یکی از انواع مدلهای یادگیری عمیق هستند که بهطور خاص برای دادههای تصویری طراحی شدهاند. این شبکهها از لایههای کانولوشنی برای یادگیری خودکار ویژگیهای سلسلهمراتبی )بزرگ به کوچک) استفاده میکنند. از لبهها و الگوهای ساده گرفته تا اشکال و اجسام پیچیدهتر. VGG16 یک معماری معروف از نوع CNN است که به دلیل سادگی و کارایی بالا شناخته میشود. این مدل از ۱۶ لایه با وزنهای قابل یادگیری تشکیل شده و از فیلترهای کانولوشنی کوچک (۳×۳) استفاده میکند. VGG16 بر روی مجموعهدادهی بزرگ ImageNet که شامل میلیون ها تصویر روزمره از پیش آموزش داده شده است و به همین دلیل قادر است ویژگیهای غنی و قابل تعمیم را از تصاویر جدید استخراج کند.
در این پروژه، از VGG16 بهعنوان استخراجکنندهی ویژگیها (Feature Extractor) استفاده میشود. بهجای استفاده از مدل برای طبقهبندی، خروجی لایههای کانولوشنی آن برای بهدستآوردن بردار ویژگی هر تصویر به کار گرفته میشود. این بردارها مهمترین ویژگیهای بصری تصاویر را در بر میگیرند و مبنایی برای خوشهبندی دادهها فراهم میکنند.
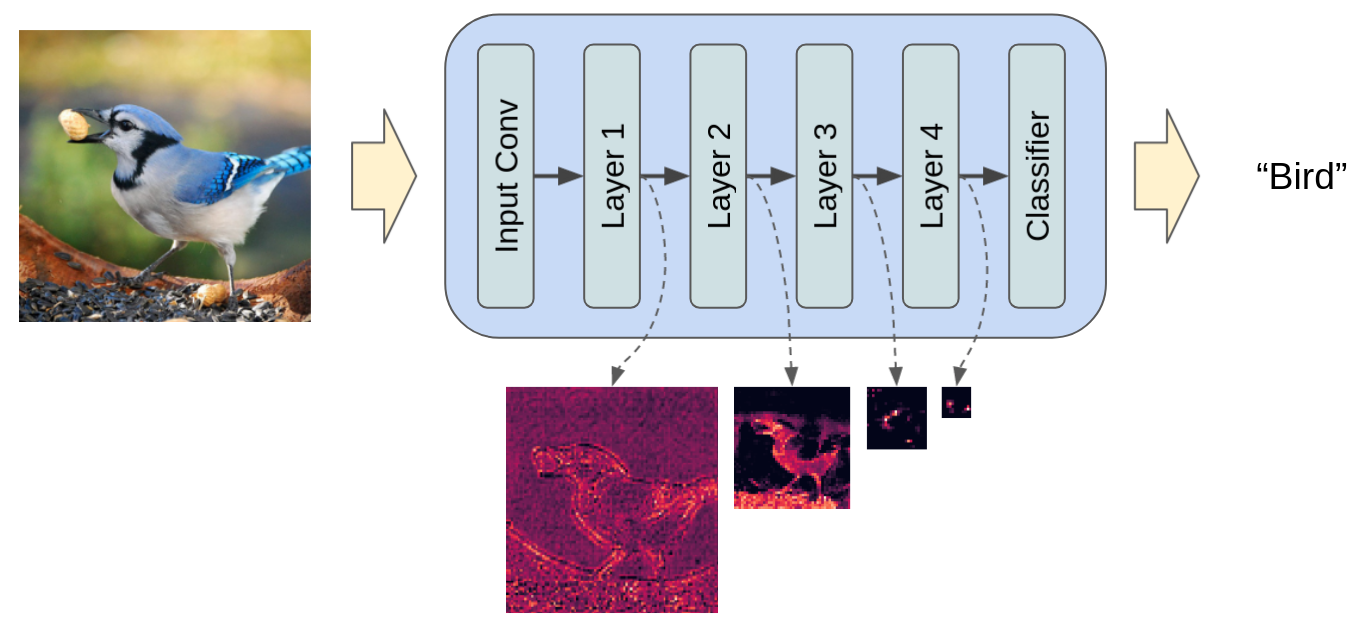
برای درک بهتر ویژگی ها میتوان تعداد از ویژگی های استخراج شده از تصاویر را مشاهده کرد

در تصویر زیر میتوان تعدادی از ویژگی های استخراج شده را مشاهده کرد :


import torch
import torchvision.models as models
import torchvision.transforms as T
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
# Load VGG16
vgg = models.vgg16(weights=models.VGG16_Weights.IMAGENET1K_V1).features.eval()
layers_to_tap = [1,2,3, 8, 15, 22, 29]
features = {}
def save_activation(name):
def hook(module, inp, out):
features[name] = out.detach().cpu()
return hook
for idx in layers_to_tap:
vgg[idx].register_forward_hook(save_activation(f"layer_{idx}"))
# Preprocess
tfms = T.Compose([
T.Resize(256),
T.CenterCrop(224),
T.ToTensor(),
T.Normalize(mean=[0.485,0.456,0.406], std=[0.229,0.224,0.225]),
])
img_path = ""
img = Image.open(img_path).convert("RGB")
plt.imshow(img)
plt.axis(False)
plt.show()
x = tfms(img).unsqueeze(0)
with torch.no_grad():
vgg(x)
def normalize_channel(arr):
arr = arr - arr.mean()
arr = arr / (arr.std() + 1e-5)
arr = arr * 64 + 128
return np.clip(arr, 0, 255).astype("uint8")
channels_to_show = 8
for name, fmap in features.items():
#[1, C, H, W]
fmap = fmap[0]
n = min(channels_to_show, fmap.shape[0])
cols = 4
rows = int(np.ceil(n / cols))
plt.figure(figsize=(cols * 4.2, rows * 4.2))
plt.suptitle(f"{name} — feature maps", y=0.98, fontsize=12)
for i in range(n):
ax = plt.subplot(rows, cols, i + 1)
chan = fmap[i].cpu().numpy()
norm_img = normalize_channel(chan)
ax.imshow(norm_img, cmap="viridis")
ax.set_xticks([]); ax.set_yticks([])
ax.set_title(f"ch {i}", fontsize=8)
plt.tight_layout()
plt.show()
plt.close()
در این پروژه هدف ما اعمال روش های مختلف بهینه سازی و توابع ضرر مختلف برای خوشه بندی تصاویر است
به عنوان نمونه در این مثال ، از تعداد ای تصاویر حیوانات استفاده میکنیم و سعی میکنیم با استفاده از ویژگی های استخراج شده از آن ها ، خوشه بندی را انجام دهیم.
در شکل زیر چند نمونه از تصاویر دیتاست را میتوان مشاهده کرد :
.jpg)
.jpg)
.jpg)
.jpg)
دانلود داده ها
این داده ها در لینک زیر قابل دانلود می باشد :
https://drive.google.com/file/d/1uPN3s1zBcmsl8oU_nOFG2MeWx4rM-Y2s/view?usp=sharing
توابع ضرر
در این قسمت به معرفی توابع ضرری که برای خوشه بندی در این تمرین استفاده میکنیم خواهیم پرداخت : برای اطلاع بیشتر و نحوه دقیق عمکلرد هر تابع به لینک های زیر مراجعه کنید
فهرست توابع ضرر
استفاده از توابع ضرر برای خوشه بندی
در مسئلهی خوشهبندی، باید «مرکز» هر خوشه را بیابیم که مجموع زیانها را کمینه کند. بسته به نوع تابع ضرر این کار میتواند به یکی از دو روش زیر انجام شود:
1. راهحلهای تحلیلی (Analytical Solutions)
برخی تابعهای ضرر فرمول ریاضی مشخصی برای مرکز بهینه دارند:
$ \mu^* = \frac{1}{n}\sum_{i=1}^n x_i $
$\mu^* = \text{median}(x_1, x_2, \ldots, x_n)$
2. بهینهسازی عددی (Numerical Optimization)
بیشتر تابعهای زیان دیگر (مثل Huber، Correntropy و …) فرمول بستهای برای $\mu^*$ ندارند، بنابراین باید از روشهای عددی برای یافتن مرکز بهینه استفاده کنیم. در بسیاری از توابع ضرر، مشتقگیری و برابر صفر قرار دادن آن منجر به یک معادله ساده مانند میانگین یا میانه نمیشود. بهعبارت دیگر، نقطهای که مجموع ضررها را کمینه میکند، ریشهی یک معادلهی غیرخطی یا حتی غیرمشتقپذیر است. به همین دلیل نمیتوان یک فرمول بسته برای مرکز خوشه نوشت و باید از روشهای بهینهسازی عددی برای پیدا کردن مقدار بهینه استفاده کرد.
در بهینهسازی عددی، ما تابع ضرر را مانند یک چشمانداز (Loss Landscape) در نظر میگیریم که هر نقطهی آن مقدار خطا را نشان میدهد. هدف الگوریتم این است که با حرکت در این چشمانداز، نقطهای را پیدا کند که کمترین مقدار را دارد. از آنجایی که شکل این چشمانداز برای توابع مختلف متفاوت است، رفتار الگوریتم و نقطهی نهایی نیز متفاوت خواهد بود.
نحوهی کار scipy.optimize.minimize:
result = minimize(objective_function, initial_guess, method='BFGS')
مقایسه 2 روش
به عنوان مثال یک نمونه از کارکرد این روش را برای یک تابع ضرر میتوان مشاهده کرد در ابتدا از یک نقطه تصادفی شروع کرده و به سمت مخالف گرادیان می رویم (گرادیان نزولی) در واقع نقطه انتخاب شده ، نقطه ای با حداقال فاصله با سایر نقاط است.
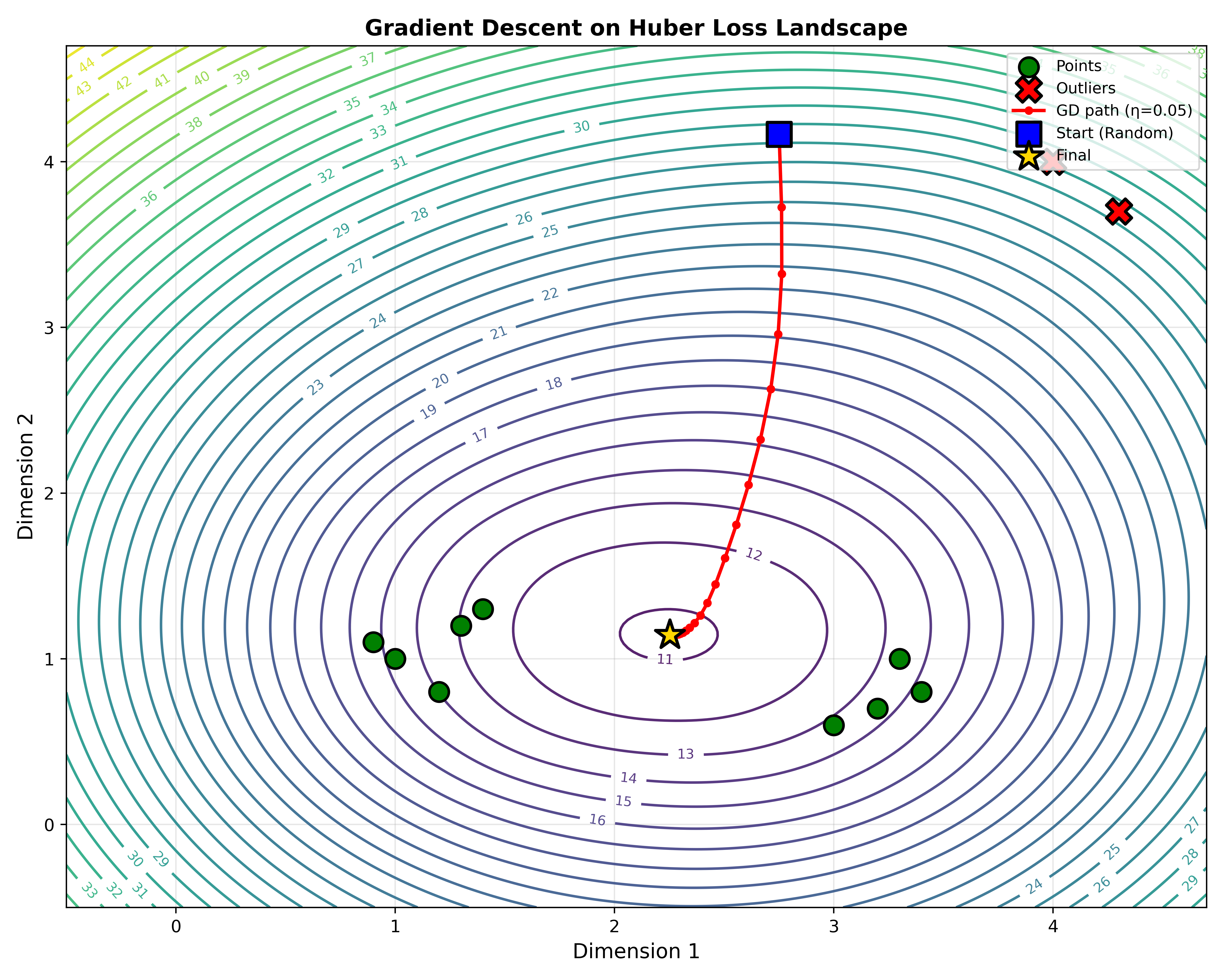
توابع با راه حل محاسباتی
تابع L2 Loss (Square Loss) → Mean
یکی از توابع بسیار پرکاربرد مورد استفاده در الگوریتم های مثل k-means
گام ۱: مشتقگیری نسبت به $\mu^*$
با استفاده از قاعدهی زنجیرهای:
$ \frac{dL}{d\mu} = \sum_{i=1}^{n} \frac{d}{d\mu}(x_i - \mu)^2 = \sum_{i=1}^{n} 2(x_i - \mu)(-1)$
$\frac{dL}{d\mu} = -2\sum_{i=1}^{n} (x_i - \mu)$
گام ۲: برابر صفر قرار دادن مشتق (شرط لازم برای کمینه)
$-2\sum_{i=1}^{n} (x_i - \mu) = 0$
$\sum_{i=1}^{n} (x_i - \mu) = 0$
گام ۳: حل برای $\mu^*$
$\sum_{i=1}^{n} x_i - \sum_{i=1}^{n} \mu = 0$
$\sum_{i=1}^{n} x_i - n\mu = 0$
$\mu^* = \frac{1}{n}\sum_{i=1}^{n} x_i$
پیاده سازی خوشه بندی با استفاده از توابع ضرر مختلف
لود کردن کتابخانه های مورد استفاده :
import torch
import torch.nn as nn
from torchvision import models, transforms
from PIL import Image
import os
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from tqdm import tqdm
لود کردن مدل vgg16 برای استخراج ویژگی
#pre-trained VGG16 model
vgg16 = models.vgg16(pretrained=True)
model = nn.Sequential(*list(vgg16.features.children()))
model.eval()
image preprocessing
preprocess = transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
اسخراج ویژگی از مجموعه داده
در این قسمت از عکس های موجود در دیتاست ، استخراج ویژگی انجام می دهیم.
def extract_features(img_path, model, device='cpu'):
image = Image.open(img_path).convert("RGB")
input_tensor = preprocess(image).unsqueeze(0).to(device)
with torch.no_grad():
features = model(input_tensor)
# Global average pooling
global_pooled = torch.mean(features, dim=(2, 3))
return global_pooled.squeeze().cpu().numpy()
def extract_features_from_folder(folder_path, model, device):
features_dict = {}
image_files = [f for f in os.listdir(folder_path)
if f.lower().endswith(('.jpg', '.jpeg', '.png'))]
image_files.sort()
print(f"Found {len(image_files)} images in '{folder_path}'")
for file in image_files:
img_path = os.path.join(folder_path, file)
print(f" Extracting features from: {file}")
features = extract_features(img_path, model, device)
features_dict[file] = features
return features_dict, image_files
image_folder = "folder name"
features_dict, image_files = extract_features_from_folder(image_folder, model)
features_list = list(features_dict.values())
data = np.stack(features_list)
تعریف توابع ضرر در کد
در این قسمت یک تابع کلی تعریف میکنیم که به عنوان ورودی اسم تابع را گرفته و فرمول آن را بر می گردانیم
def get_loss_func(loss_type, params={}):
if loss_type == 'square':
def loss(x, mu):
return np.sum((x - mu)**2)
return loss
elif loss_type == 'absolute':
def loss(x, mu):
return np.sum(np.abs(x - mu))
return loss
elif loss_type == 'huber':
delta = params.get('delta', 1.0)
def loss(x, mu):
res = np.abs(x - mu)
return np.sum(np.where(res <= delta,
0.5 * res**2,
delta * (res - 0.5 * delta)))
return loss
elif loss_type == 'pseudo_huber':
delta = params.get('delta', 1.0)
def loss(x, mu):
res = x - mu
return np.sum(delta**2 * (np.sqrt(1 + (res / delta)**2) - 1))
return loss
elif loss_type == 'correntropy':
sigma = params.get('sigma', 1.0)
def loss(x, mu):
d2 = np.sum((x - mu)**2)
return 1 - np.exp(-d2 / (2 * sigma**2))
return loss
elif loss_type == 'epsilon_insensitive':
epsilon = params.get('epsilon', 1.0)
def loss(x, mu):
d = np.linalg.norm(x - mu)
return max(0, d - epsilon)
return loss
الگوریتم خوشه بندی
برای آشنایی بیشتر با خوشه بندی و روش های آن به لینک زیر مراحعه کنید :
مقدمات خوشه بندی و فرموله کردن مسئله
مراحل خوشنه بندی و استفاده از توابع ضرر مختلف
پیاده سازی
def update_center(points, loss_type, params):
if len(points) == 0:
return np.zeros(points.shape[1])
if loss_type == 'square':
return np.mean(points, axis=0)
elif loss_type == 'absolute':
return np.median(points, axis=0)
else:
def objective(mu):
loss_func = get_loss_func(loss_type, params)
total_loss = sum(loss_func(x, mu) for x in points)
return total_loss
initial_guess = np.mean(points, axis=0)
result = minimize(
objective,
initial_guess,
method='BFGS',
options={'maxiter': 20}
)
return result.x
def generalized_clustering(data, k, loss_type, params={}, max_iter=3, tol=1e-4):
n, d = data.shape
centers = data[np.random.choice(n, k, replace=False)]
prev_shift = np.inf
for iter in range(max_iter):
# Assign each point to nearest center
dists = np.array([[get_loss_func(loss_type, params)(data[i], centers[j])
for j in range(k)]
for i in range(n)])
labels = np.argmin(dists, axis=1)
# Update centers
new_centers = np.zeros((k, d))
for j in tqdm(range(k), desc=f"Updating centers (iter {iter+1})"):
points_j = data[labels == j]
if len(points_j) > 0:
new_centers[j] = update_center(points_j, loss_type, params)
# Check convergence
shift = np.sum(np.linalg.norm(new_centers - centers, axis=1))
centers = new_centers
if shift < tol or abs(shift - prev_shift) < 1e-6:
print(f" Converged after {iter+1} iterations")
break
prev_shift = shift
return centers, labels
def find_closest_image(center, points, indices, loss_func):
min_dist = np.inf
closest_idx = -1
for idx, p in zip(indices, points):
dist = loss_func(p, center)
if dist < min_dist:
min_dist = dist
closest_idx = idx
return closest_idx
def plot_representatives(loss_type, centers, labels, image_files, folder_path, loss_func):
fig, axs = plt.subplots(1, len(centers), figsize=(5 * len(centers), 5))
fig.suptitle(f'Representative Images - {loss_type.upper()} Loss', fontsize=16, fontweight='bold')
for j, center in enumerate(centers):
# Find all images in this cluster
cluster_indices = [i for i in range(len(labels)) if labels[i] == j]
cluster_points = data[cluster_indices]
if len(cluster_points) > 0:
# Find the image closest to the center
closest_i = find_closest_image(center, cluster_points, cluster_indices, loss_func)
img_file = image_files[closest_i]
img_path = os.path.join(folder_path, img_file)
img = mpimg.imread(img_path)
if len(centers) == 1:
axs.imshow(img)
axs.set_title(f'Representative {j+1}\n{img_file}', fontsize=12)
axs.axis('off')
else:
axs[j].imshow(img)
axs[j].set_title(f'Representative {j+1}\n{img_file}', fontsize=12)
axs[j].axis('off')
plt.tight_layout()
plt.show()
نتایج خوشه بندی
در این بخش به بررسی نتایج خوشه بندی با استفاده از توابع ضرر مختلف می پردازیم
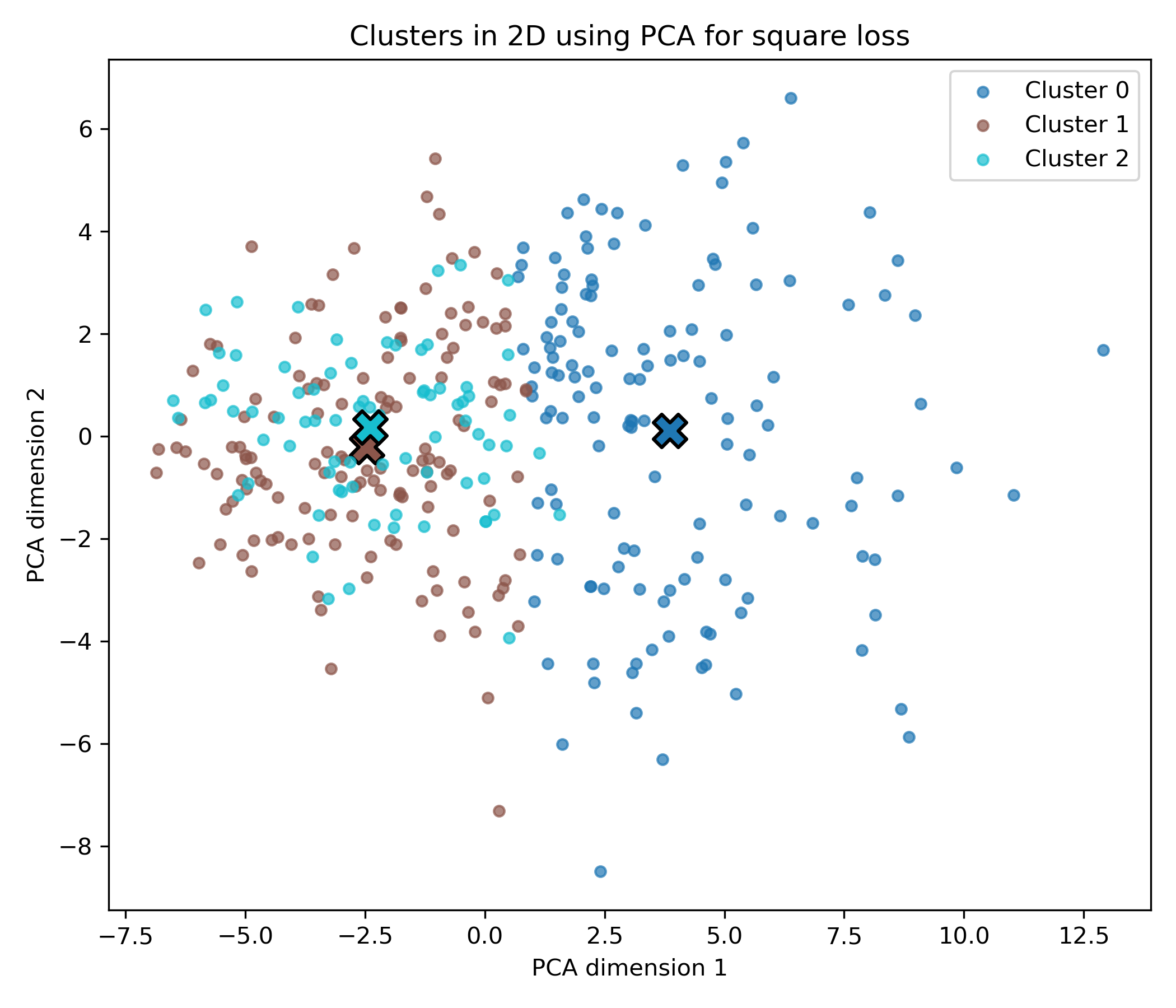
تابع L2
loss_type = 'square'
params = params_dict[loss_type]
z=(f"🔄 Running clustering with {loss_type.upper()} loss...")
centers, labels = generalized_clustering(data, k, loss_type, params)
loss_func = get_loss_func(loss_type, params)
plot_representatives(loss_type, centers, labels, image_files, image_folder, loss_func,z)

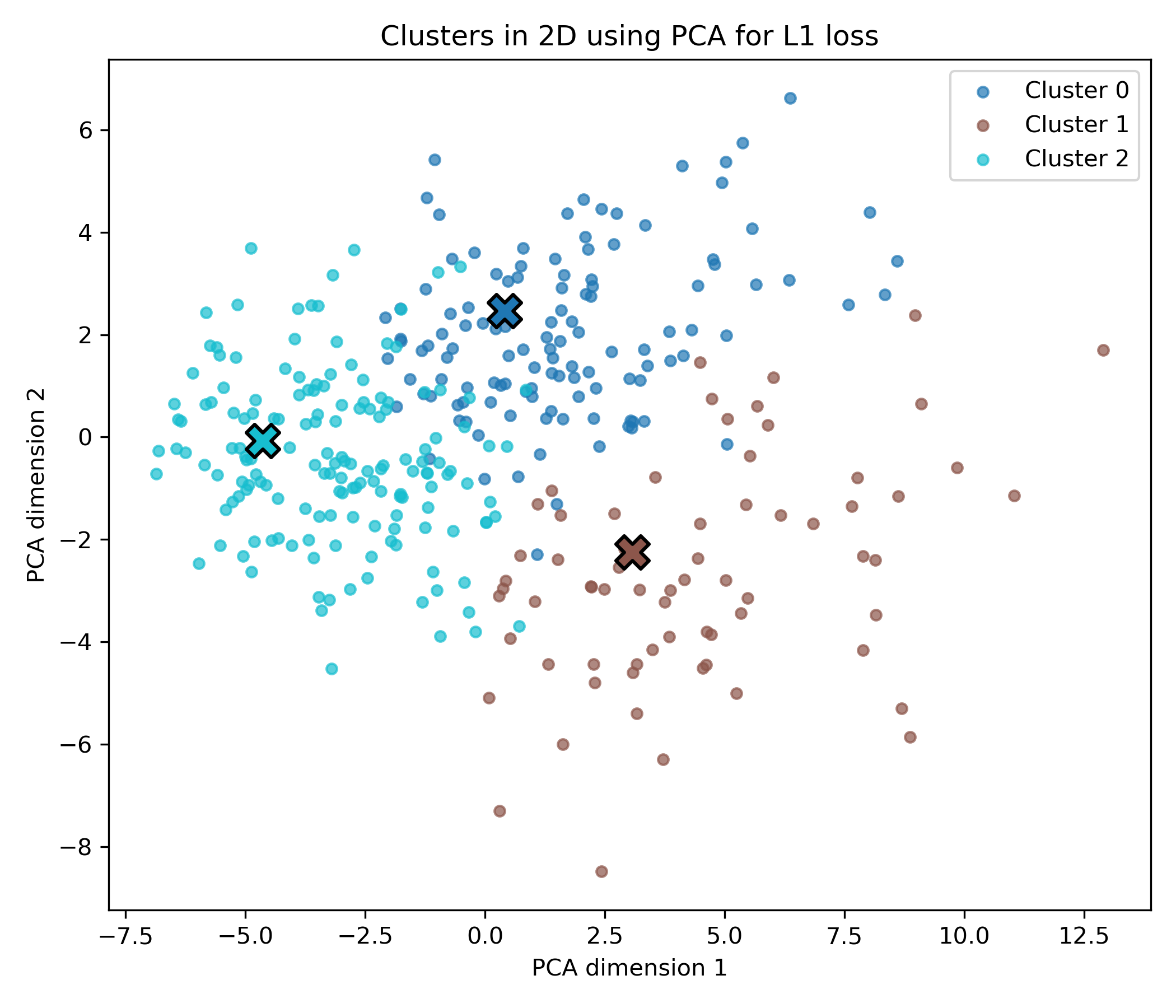
تابع L1
loss_type = 'absolute'
params = params_dict[loss_type]
z=(f"🔄 Running clustering with {loss_type.upper()} loss...")
centers, labels = generalized_clustering(data, k, loss_type, params)
loss_func = get_loss_func(loss_type, params)
plot_representatives(loss_type, centers, labels, image_files, image_folder, loss_func,z)

تابع Huber
loss_type = 'huber'
params = params_dict[loss_type]
z=(f"🔄 Running clustering with {loss_type.upper()} loss...")
centers, labels = generalized_clustering(data, k, loss_type, params)
loss_func = get_loss_func(loss_type, params)
plot_representatives(loss_type, centers, labels, image_files, image_folder, loss_func,z)


تابع Pseudo-Huber
loss_type = 'pseudo-huber'
params = params_dict[loss_type]
z=(f"🔄 Running clustering with {loss_type.upper()} loss...")
centers, labels = generalized_clustering(data, k, loss_type, params)
loss_func = get_loss_func(loss_type, params)
plot_representatives(loss_type, centers, labels, image_files, image_folder, loss_func,z)


تابع Correntropy
loss_type = 'correntropy'
params = params_dict[loss_type]
z=(f"🔄 Running clustering with {loss_type.upper()} loss...")
centers, labels = generalized_clustering(data, k, loss_type, params)
loss_func = get_loss_func(loss_type, params)
plot_representatives(loss_type, centers, labels, image_files, image_folder, loss_func,z)


تابع Epsilon-Insensitive
loss_type = 'epsilon_insensitive'
params = params_dict[loss_type]
z=(f"🔄 Running clustering with {loss_type.upper()} loss...")
centers, labels = generalized_clustering(data, k, loss_type, params)
loss_func = get_loss_func(loss_type, params)
plot_representatives(loss_type, centers, labels, image_files, image_folder, loss_func,z)


نتایج
در بخش نتایج، با نمایش تصاویر نمایندهی هر خوشه برای توابع ضرر مختلف، میتوانیم بهصورت شهودی ببینیم که شبکهی VGG16 چه ساختاری را در فضای ویژگیها آموخته است. هر تصویری که بهعنوان «مرکز خوشه» نمایش داده میشود، در واقع نمونهای است که کمترین فاصله را با سایر تصاویر آن خوشه در فضای ویژگی دارد و میتوان آن را نمایندهی بصری آن گروه دانست. زمانی که یک تصویر در چند تابع ضرر مختلف بهعنوان مرکز خوشه تکرار میشود، این موضوع نشان میدهد که آن نمونه در فضای ویژگیها یک نمونهی پایدار و مستقل از جزئیات انتخاب تابع ضرر، ساختار کلی خوشهها حول آن شکل میگیرد. از طرف دیگر، تفاوت بین تصاویر نماینده در توابع ضرر مختلف بیانگر این است که نحوهی اندازهگیری فاصله و خطا میتواند بر مرزبندی خوشهها اثر بگذارد، هرچند محتوای کلی خوشهها (مثلاً نوع حیوان یا زاویهی دید) معمولاً ثابت میماند. به این ترتیب، مشاهدهی مستقیم مراکز خوشه کمک میکند تا علاوه بر تحلیل عددی، درک شهودی و بصری بهتری از کیفیت خوشهبندی و معنای هر خوشه در سطح تصویر بهدست آوریم.
منابع
- http://cnnlocalization.csail.mit.edu/
- https://docs.pytorch.org/vision/main/models.html
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
- https://arxiv.org/abs/1409.1556
