مدلهای باتری
نویسنده: سپهر جفرزاده
دانشگاه فردوسی مشهد
مقدمه
تاریخچه
لوئیجی گالوانی اولین کسی بود که متوجه شد قرار دادن فلزات خاصی در تماس با یکدیگر میتواند منجر به ایجاد اختلاف پتانسیل الکتریکی شود (یا به عبارت دقیقتر، میتواند باعث پرش پای قورباغه مرده شود، که امروزه میدانیم ناشی از اختلاف پتانسیل ایجاد شده توسط فلزات است). گالوانی اولین “سلول الکتروشیمیایی” را ساخت. الساندرو ولتا سپس چندین از این سلولها را با هم ترکیب کرد تا “پیل ولتایی” را تشکیل دهد، که امروزه آن را باتری مینامیم.
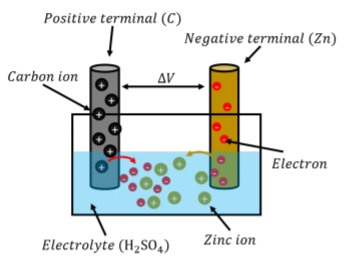
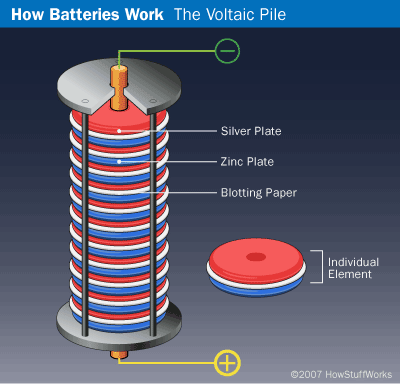
باتری در یک مدار چیست؟
باتری به دستگاهی اطلاق میشود که میتواند یک اختلاف پتانسیل ثابت بین دو ترمینال ایجاد کند. با این حال، آزمایشها نشان میدهند که اختلاف پتانسیل در سراسر ترمینالهای یک باتری همیشه برابر با اختلاف پتانسیل در سراسر باتری ایدهآل نیست و عوامل متعددی میتوانند بر آن تأثیر بگذارند.
import schemdraw
from schemdraw import elements as e
with schemdraw.Drawing() as d:
e.Gap().down().label('$V_t$')
line = e.Line().left().idot(open=True)
voltage_source = e.SourceV().up().label('$V_s$')
e.Line().right().dot(open=True)
چرا از مدلهای باتری استفاده میکنیم؟
ما از مدلهای باتری استفاده میکنیم تا بتوانیم رفتار باتریها را در موقعیتهای مختلف توصیف کنیم. روشهای مختلفی برای مدلسازی یک باتری وجود دارد: مدل مدار معادل (ECM)، مدلهای حرارتی، مدلهای الکتروشیمیایی و غیره. ما در این پروژه از ECM استفاده خواهیم کرد. در این نوع مدلسازی، از المانهای الکتریکی (مانند مقاومت و خازن) برای توصیف رفتار باتریها استفاده میکنیم.
مدل Rint
توضیح مدل Rint
این مدل سادهترین و پایهایترین مدل مدار معادل است. این مدل از یک باتری ایدهآل با ولتاژ مدار باز $V_s$ و یک مقاومت داخلی ثابت $R_{int}$ تشکیل شده است. مقاومت داخلی به این دلیل وجود دارد که موادی که باتری را میسازند خود دارای مقاومت هستند. برای مثال، اگر الکترونها بخواهند میله روی در سلول الکتریکی را ترک کنند، هنگام عبور از روی مقداری انرژی از دست میدهند. این بدان معناست که اگر جریان افزایش یابد، الکترونها انرژی بیشتری از دست میدهند، بنابراین باتری ولتاژ کمتری ایجاد میکند.
import schemdraw
from schemdraw import elements as e
with schemdraw.Drawing() as d:
e.Gap().down().label('$V_t$')
line = e.Line().left().idot(open=True)
voltage_source = e.SourceV().up().label('$V_s$')
internal_resistor = e.Resistor().right().label('$R_{int}$').dot(open=True)
تحلیل مدل Rint
برای مشاهده چگونگی تأثیر $R_{int}$ بر ولتاژ خروجی باتری $V_t$، یک تحلیل DC سوئیپ روی مدار انجام میدهیم.
import schemdraw
from schemdraw import elements as e
with schemdraw.Drawing() as d:
line1 = e.Line().right()
e.SourcePulse().down().label('Current\nPulse')
line2 = e.Line().left().idot(open=True)
line3 = e.Line().left()
voltage_source = e.SourceV().up().label('$V_s$')
internal_resistor = e.Resistor().right().label('$R_{int}$').dot(open=True)
voltmeter = e.MeterV().at(internal_resistor.end).down() # Adding the voltmeter between the two dots
line = e.Line().at(internal_resistor.end).right()
e.CurrentLabelInline().at(internal_resistor).label('I')
import matplotlib.pyplot as plt
from PySpice.Spice.Netlist import Circuit
from PySpice.Unit import *
from PySpice.Probe.Plot import plt as spice_plot
circuit = Circuit('Experiment on R_int model with variable current source')
# DC voltage source (Vs), internal resistance (R_int)
V_s = 12 @ u_V # Example DC source voltage of 10V
R_int = 10 @ u_Ohm # Internal resistance of 50 Ohms
circuit.V(1, 'n1', circuit.gnd, V_s)
circuit.R(1, 'n1', 'n2', R_int)
# pulse current source (current_pulse)
# PULSE parameters: (I1, I2, Delay, Rise Time, Fall Time, Pulse Width, Period)
current_pulse = circuit.I(1, 'n2', circuit.gnd, 'PULSE(0 1A 0s 1ms 1ms 5ms 10ms)')
# Run transient analysis
simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.transient(step_time=0.1 @ u_ms, end_time=60 @ u_ms)
plt.figure(figsize=(10, 8))
# Plot Terminal Voltage over time
plt.subplot(211)
plt.plot(analysis.nodes['n2'])
plt.title('Terminal Voltage (V) vs Time (s)')
plt.xlabel('Time [0.1 ms]')
plt.ylabel('Voltage [V]')
# Plot Current through the current source over time
plt.subplot(212)
plt.plot(analysis.branches['v1'])
plt.title('Current (A) vs Time (s)')
plt.xlabel('Time [0.1 ms]')
plt.ylabel('Current [A]')
plt.tight_layout()
plt.show()
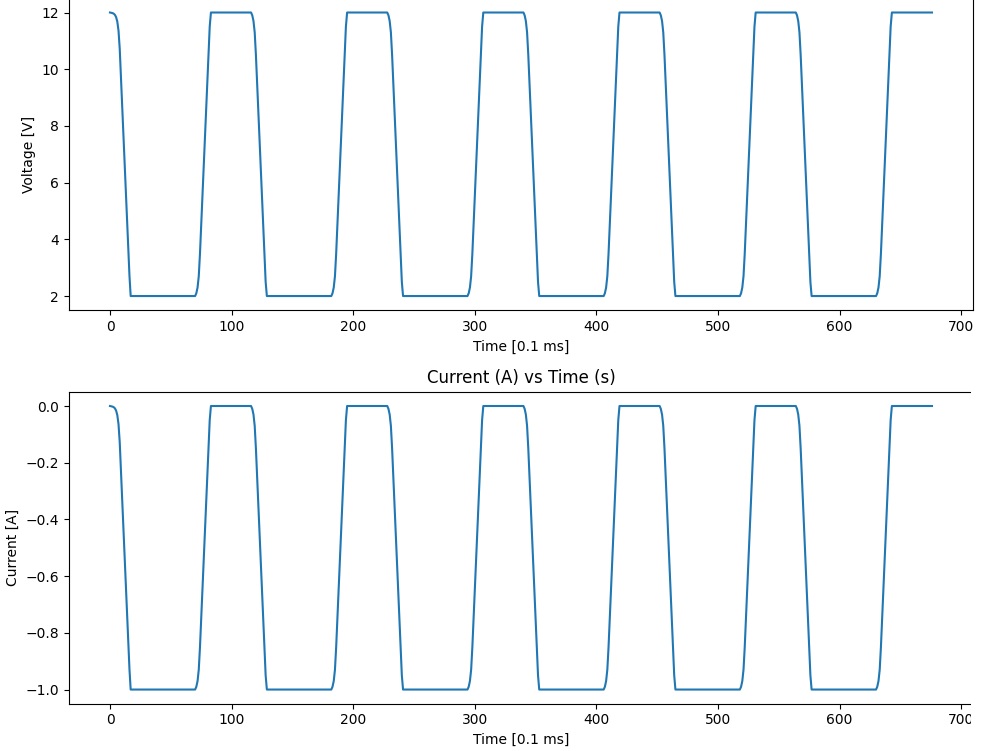
محاسبات در مدل Rint
ولتاژ اندازهگیری شده در دو سر مقاومت بار $V_{(t)}$، را میتوان با استفاده از قانون اهم محاسبه کرد.
با توجه به مدار:
- $V_s$: ولتاژ مدار باز باتری (که به آن ولتاژ تونن نیز میگویند)
- $R_{int}$: مقاومت داخلی باتری
- $R_{load}$: مقاومت بار خارجی
ولتاژ در دو سر مقاومت بار $V_{(t)}$ به صورت زیر محاسبه میشود:
\[\begin{align*} V(t) &= V_0 - R_{int} \times I(t) \\ V_t &= \frac{R_{load}}{R_{int} + R_{load}} \times V_s \\ I(t) &= \frac{V(t)}{R_{load}} \end{align*}\]معادله دوم نشان میدهد که با افزایش مقاومت بار، ولتاژ ترمینال به $V_s$ نزدیک میشود. برعکس، با کاهش مقاومت بار، $V_{(t)}$ به دلیل افت ولتاژ در $R_{int}$ کاهش مییابد.
در این شبیهسازی، مشاهده کردیم که چگونه ولتاژ ترمینال $V_{(t)}$ با مقاومتهای بار مختلف تغییر میکند.
مدل RC مرتبه دوم
توضیح مدل RC مرتبه دوم
در این مدل، دو جفت RC داریم، یکی با ثابت زمانی کم $C \times R$ ($C_s$ و $R_s$، ‘s’ مخفف کوتاهمدت) و دیگری با ثابت زمانی بالا $C \times R$ ($C_l$ و $R_l$، ‘l’ مخفف بلندمدت) در کنار مقاومت داخلی. هنگامی که جریان عبوری از یک باتری تغییر میکند، پاسخ به این تغییر غیرخطی است. جفت RC کوتاهمدت به طور کلی نمایانگر پاسخ دینامیکی فوری باتری به تغییرات بار است. و جفت RC بلندمدت نشاندهنده دینامیکهای کندتر پاسخ باتری است که اثرات و رفتارهای بلندمدت را ثبت میکند.
import schemdraw
from jedi.inference.utils import unite
from schemdraw import elements as e
with schemdraw.Drawing() as d:
e.Gap().down().label('$V_t$')
e.Line().left().length(11).idot()
voltage_source = e.SourceV().up().label('$V_{OC}$')
internal_resistor = e.Resistor().right().label('$R_{int}$')
e.Line().up().length(1)
capacitor_s = e.Capacitor().right().label('$C_{s}$')
line = e.Line().down().length(1)
e.Line().down().length(1)
resistor_s = e.Resistor().left().label('$R_{s}$')
e.Line().up().length(1)
e.Line().at(line.end).right().length(1)
e.Line().up().length(1)
capacitor_l = e.Capacitor().right().label('$C_{l}$')
line = e.Line().down().length(1)
e.Line().down().length(1)
resistor_l = e.Resistor().left().label('$R_{l}$')
e.Line().up().length(1)
e.Line().at(line.end).right().length(1).dot()
e.CurrentLabelInline().at(internal_resistor).label('$I_{bat}$')
تحلیل مدل RC مرتبه دوم
برای مشاهده چگونگی تأثیر دو جفت RC موازی بر ولتاژ ترمینال، یک تحلیل گذرا روی این مدار انجام خواهیم داد.
import schemdraw
from jedi.inference.utils import unite
from schemdraw import elements as e
with schemdraw.Drawing() as d:
line1 = e.Line().left().length(11)
voltage_source = e.SourceV().up().label('$V_{OC}$')
internal_resistor = e.Resistor().right().label('$R_{int}$')
e.Line().up().length(1)
capacitor_s = e.Capacitor().right().label('$C_{s}$')
line = e.Line().down().length(1)
e.Line().down().length(1)
resistor_s = e.Resistor().left().label('$R_{s}$')
e.Line().up().length(1)
e.Line().at(line.end).right().length(1)
e.Line().up().length(1)
capacitor_l = e.Capacitor().right().label('$C_{l}$')
line = e.Line().down().length(1)
e.Line().down().length(1)
resistor_l = e.Resistor().left().label('$R_{l}$')
e.Line().up().length(1)
e.Line().at(line.end).right().length(1)
e.MeterV().down()
e.Line().right()
e.SourcePulse().up().label('Current\nPulse')
e.Line().left()
e.CurrentLabelInline().at(internal_resistor).label('$I_{bat}$')
from PySpice.Spice.Netlist import Circuit
from PySpice.Unit import *
from PySpice.Probe.Plot import plt
# Create the Thevenin-based RC model with a variable current source
circuit = Circuit('Thevenin RC Model with Pulse Current Source')
# Define voltage source for open circuit voltage (Voc)
V_oc = 12@u_V # Example battery voltage
circuit.V(1, 'node1', circuit.gnd, V_oc)
# Internal resistance (R0)
R_0 = 0.1@u_Ohm
circuit.R(1, 'node1', 'node2', R_0)
# RC pair: R1 and C1
R_1 = 0.2@u_Ohm
C_1 = 15@u_mF
circuit.R(2, 'node2', 'node3', R_1)
circuit.C(1, 'node2', 'node3', C_1)
# RC pair: R2 and C2
R_2 = 0.8@u_Ohm
C_2 = 200@u_mF
circuit.R(3, 'node3', 'node4', R_2)
circuit.C(2, 'node3', 'node4', C_2)
# Add an independent current source with a PULSE signal
circuit.I(1, 'node4', circuit.gnd, 'PULSE(0A 5A 1ms 1ms 1ms 10ms 20ms)')
# Run the transient analysis for 50 ms
simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.transient(step_time=0.1@u_ms, end_time=60@u_ms)
# Plot the terminal voltage (node1 to ground) and current over time
plt.figure(1)
# Voltage at node1 (battery terminal)
plt.subplot(211)
plt.plot(analysis.nodes['node3'])
plt.title('Terminal Voltage (V) vs Time (s)')
plt.xlabel('Time [s]')
plt.ylabel('Voltage [V]')
plt.grid()
# Access the current probe for 'I1' (the current source)
plt.subplot(212)
plt.plot(analysis.branches['v1'])
plt.title('Current (A) vs Time (s)')
plt.xlabel('Time [s]')
plt.ylabel('Current [A]')
plt.grid()
plt.tight_layout()
plt.show()
محاسبات در مدل RC مرتبه دوم
با اعمال معادلات کیرشهوف به این مدار:
\[\begin{align*} V_{C_s}(t+1) &= V_{C_s}(t) \times e^{-\frac{T}{C_s \times R_s}} + R_s \times I_{Batt}(t) \times \left(1 - e^{-\frac{T}{C_s \times R_s}}\right) \\ V_{C_l}(t+1) &= V_{C_l}(t) \times e^{-\frac{T}{C_l \times R_l}} + R_l \times I_{Batt}(t) \times \left(1 - e^{-\frac{T}{C_l \times R_l}}\right) \\ V_{Batt} &= V_{OC}(SOC) - V_{C_l}(t) - V_{C_s}(t) - R_{series} \times I_{Batt} \end{align*}\]که در آن $T$ نشاندهنده گام زمانی و $t$ نشاندهنده زمان شبیهسازی است. $V_{C_L}$ و $V_{C_s}$ پاسخ گذرا با مدت زمان بلندمدت و کوتاهمدت هستند (ولتاژ دو سر $C_l$ و $C_s$).
نتیجهگیری
هدف از این تکلیف، ارائه درک عمیقتری از رفتار باتری بود، به ویژه اینکه مدلسازی دقیق ویژگیهای دینامیکی آنها چقدر میتواند چالشبرانگیز باشد. همانطور که دیدیم، پیشبینی عملکرد یک باتری تحت شرایط مختلف پیچیده است. با این حال، پژوهشگران به طور مداوم در حال توسعه روشهایی، مانند مدلهای مدار معادل (ECM)، برای تقریب هرچه بیشتر این رفتارها هستند.
شایان ذکر است که هیچ رویکرد مدلسازی واحدی نمیتواند هر جنبه از دینامیک باتری را به طور کامل ثبت کند. برای نتایج دقیقتر، اغلب لازم است چندین تکنیک مدلسازی با هم ترکیب شوند.
