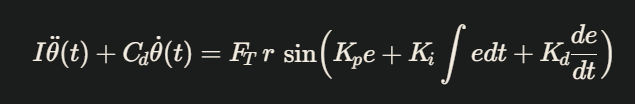هدایت موشک با کنترلر PID
اطلاعات نویسنده
نام: سید محمدرضا حسینی
وابستگی: گروه مهندسی کامپیوتر، دانشگاه فردوسی مشهد
تماس: eprogramer2020@gmail.com
۱. مقدمه: چرا موشک به PID نیاز دارد؟
هدف این پروژه، بررسی و درک چگونگی استفاده از کنترلرهای PID برای هدایت دقیق یک موشک در مسیر پروازی تعیینشدهی آن است.
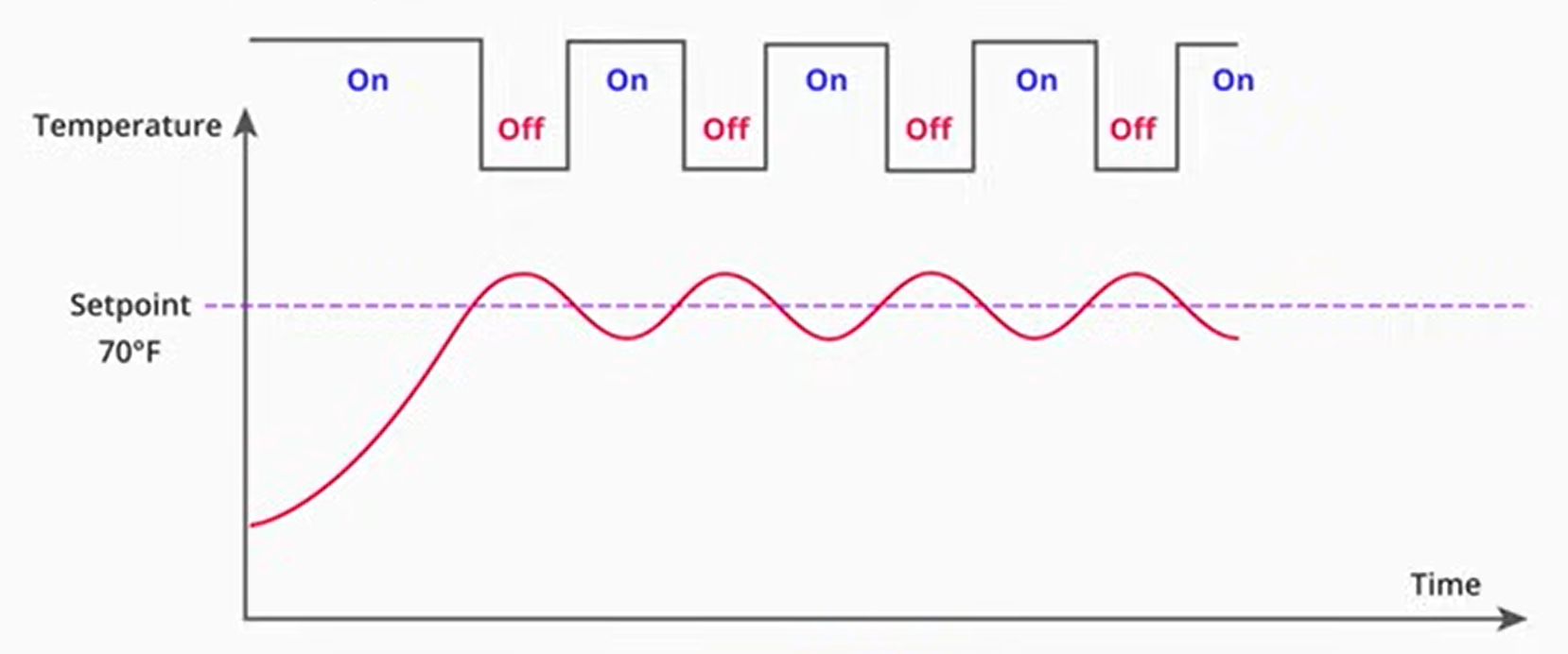
در سادهترین حالت، برای کنترل یک سیستم میتوان از یک کنترلر «روشن/خاموش» (On/Off) استفاده کرد.
- مثال: سیستم تهویه مطبوع خانه. اگر دما ۲ درجه گرم باشد، کولر با ۱۰۰٪ توان روشن میشود. وقتی به دمای مطلوب رسید، با ۱۰۰٪ توان خاموش میشود.
- مشکل: این روش برای موشک فاجعهبار است. اگر موشک ۱ درجه منحرف شود، عملگرها (مثلاً نازل) با تمام قدرت فعال میشوند و موشک را به شدت به سمت دیگر میبرند (Overshoot). این فرآیند «کوبشی» (Bang-bang) دائماً تکرار میشود، سوخت زیادی مصرف میکند و پروازی بسیار ناپایدار و خشن ایجاد میکند.
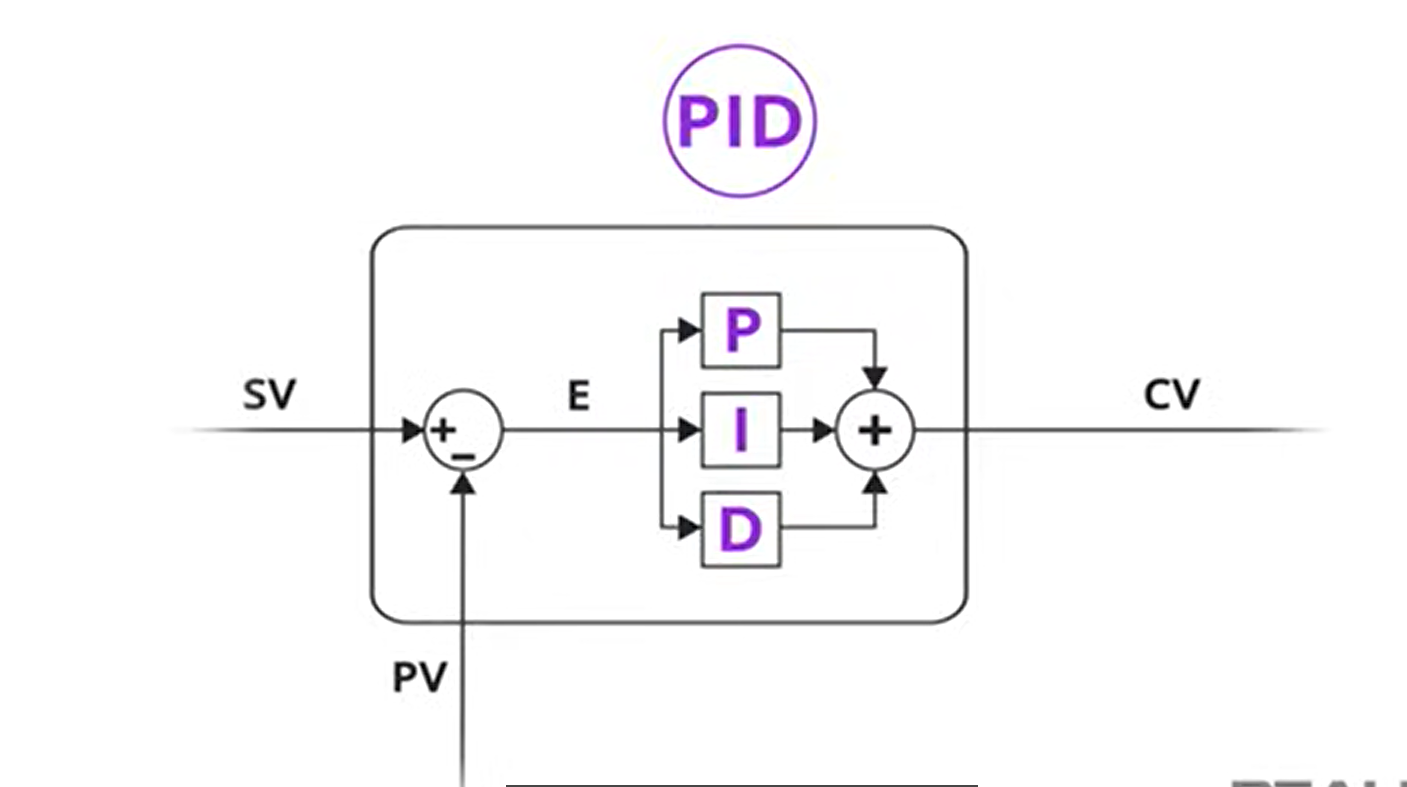
اینجاست که کنترلر PID (تناسبی-انتگرالی-مشتقی) وارد میشود. برخلاف سیستم روشن/خاموش، PID یک سیستم کنترلی «هوشمند» و «نرم» است.
- مزیت اصلی: PID به سادگی «روشن» یا «خاموش» نمیشود. PID میداند که «چقدر» از هدف دور است و «با چه سرعتی» در حال دور شدن است.
- عملکرد: اگر موشک کمی منحرف شود، PID فرمان کوچکی برای اصلاح میدهد. اگر خیلی منحرف شود، فرمان بزرگتری میدهد. این رویکرد تناسبی، پروازی نرم، پایدار و بهینه را تضمین میکند.
۲. کشف PID: ساخت یک مغز هوشمند در سه مرحله
برای هدایت یک موشک، ما به یک «مغز» یا کنترلر نیاز داریم. بیایید این مغز را از سادهترین حالت ممکن بسازیم و گام به گام آن را هوشمندتر کنیم.
🧠 مرحله ۱: مغزِ «حالنگر» (کنترلر P)
اولین ایدهی ما یک کنترلر ساده «تناسبی» (Proportional) یا P است.
- کارش چیست؟ این مغز فقط به «الان» نگاه میکند. منطق آن ساده است: «هرچقدر از هدف دورتری، من هم محکمتر هل میدهم.»
- مثال: فرض کنید هدف، زاویه ۰ درجه است.
- اگر موشک
۲ درجه منحرف شود، P با ۱۰ واحد نیرو فرمان اصلاح میدهد.
- اگر موشک
۴ درجه منحرف شود، P با ۲۰ واحد نیرو فرمان میدهد.
- مشکل این مغز (The Problem): این مغز «تنبل» است و یک مشکل اساسی دارد: خطای حالت پایدار (Steady-State Error).
- علت مشکل: تصور کنید برای صاف نگه داشتن موشک در برابر یک باد جانبی ملایم، به
۵ واحد نیروی دائمی نیاز است. مغز P میگوید: «من فقط زمانی نیرو تولید میکنم که “خطا” وجود داشته باشد.»
در نتیجه، موشک هرگز به ۰ درجه واقعی نمیرسد! بلکه روی ۰.۵ درجه خطا میماند، چون این خطای کوچک ۰.۵ درجهای لازم است تا کنترلر P، آن ۵ واحد نیروی مورد نیاز را تولید کند.
🧠🧠 مرحله ۲: اضافه کردن «حافظه» (کنترلر PI)
ما باید مشکل «تنبل» بودن P را حل کنیم. برای این کار، یک مغز جدید با قابلیت «حافظه» به آن اضافه میکنیم: کنترلر «انتگرالی» (Integral) یا I.
- کارش چیست؟ این مغز «گذشتهنگر» و بسیار «کلهشق» است. این بخش خطاهای گذشته را «جمع میزند».
- چرا «انتگرال»؟ در ریاضیات، «انتگرال» به معنای «جمع کردن» مقادیر در طول زمان است. این کنترلر دقیقاً همین کار را میکند.
- راهحل: کنترلر I به آن خطای کوچک
۰.۵ درجهای که P نادیده گرفته بود نگاه میکند و میگوید:
- «ثانیه اول: خطا ۰.۵ است. (جمع = ۰.۵)»
- «ثانیه دوم: خطا هنوز ۰.۵ است. (جمع = ۱.۰)»
- «ثانیه سوم: خطا هنوز ۰.۵ است. (جمع = ۱.۵)»
این «جمع انباشتهشده» (integral_sum) باعث میشود نیروی فرمان I لحظه به لحظه قویتر شود تا زمانی که آنقدر نیرو اعمال کند که خطا دقیقاً به صفر برسد.
- مشکل جدید: این مغز جدید (PI) اگرچه دقیق است، اما «بیشفعال» است و باعث «بیشجهش» (Overshoot) میشود.
- علت مشکل: تا زمانی که موشک به ۰ درجه برسد، کنترلر I مقدار زیادی نیرو در خود «انباشته» کرده است. وقتی موشک به هدف میرسد، I نمیتواند به سرعت فرمان خود را صفر کند. این نیروی انباشتهشده باعث میشود موشک با سرعت از هدف عبور کند و به سمت دیگر منحرف شود. این باعث نوسان میشود.
🧠🧠🧠 مرحله ۳: اضافه کردن «ترمز» (کنترلر PID)
ما اکنون یک سیستم دقیق (به لطف I) اما نوسانی داریم. ما به یک «ترمز» هوشمند نیاز داریم. این ترمز، کنترلر «مشتقی» (Derivative) یا D است.
- کارش چیست؟ این مغز «آیندهنگر» است. به اینکه الان کجا هستیم (خطا) یا در گذشته کجا بودهایم (انتگرال) اهمیتی نمیدهد. فقط به یک چیز اهمیت میدهد: «سرعت تغییر خطا چقدر است؟»
- چرا «مشتق»؟ در ریاضیات، «مشتق» دقیقاً به معنای «نرخ لحظهای تغییرات» یا همان «سرعت» است.
- راهحل:
- وقتی موشک با سرعت زیاد به سمت هدف (خطای صفر) حرکت میکند، کنترلر D (آیندهنگر) متوجه میشود: «خطر! داریم خیلی سریع به هدف نزدیک میشویم! اگر ادامه دهیم، قطعاً از آن رد خواهیم شد (Overshoot)!»
- در این لحظه، D به عنوان «ترمز» عمل میکند و یک فرمان در جهت مخالف حرکت اعمال میکند تا سرعت را بگیرد و موشک را به نرمی روی هدف (صفر درجه) بنشاند.
خلاصه: تیم کامل (P + I + D)
حالا ما یک «مغز» کامل و هوشمند داریم که مانند یک تیم سهنفره کار میکند:
. P (تناسبی): به خطای فعلی واکنش نشان میدهد. (واکنش سریع)
. I (انتگرالی): خطاهای انباشتهشده گذشته را از بین میبرد. (دقت بالا)
. D (مشتقی): سرعت نزدیک شدن به هدف در آینده را پیشبینی کرده و جلوی نوسان را میگیرد. (پایداری و نرمی)
این سه با هم همکاری میکنند تا موشک را سریع، دقیق و پایدار به مقصد برسانند.
</div>
## ۳. طرز کار PID در موشک (تشریح حلقه بسته)
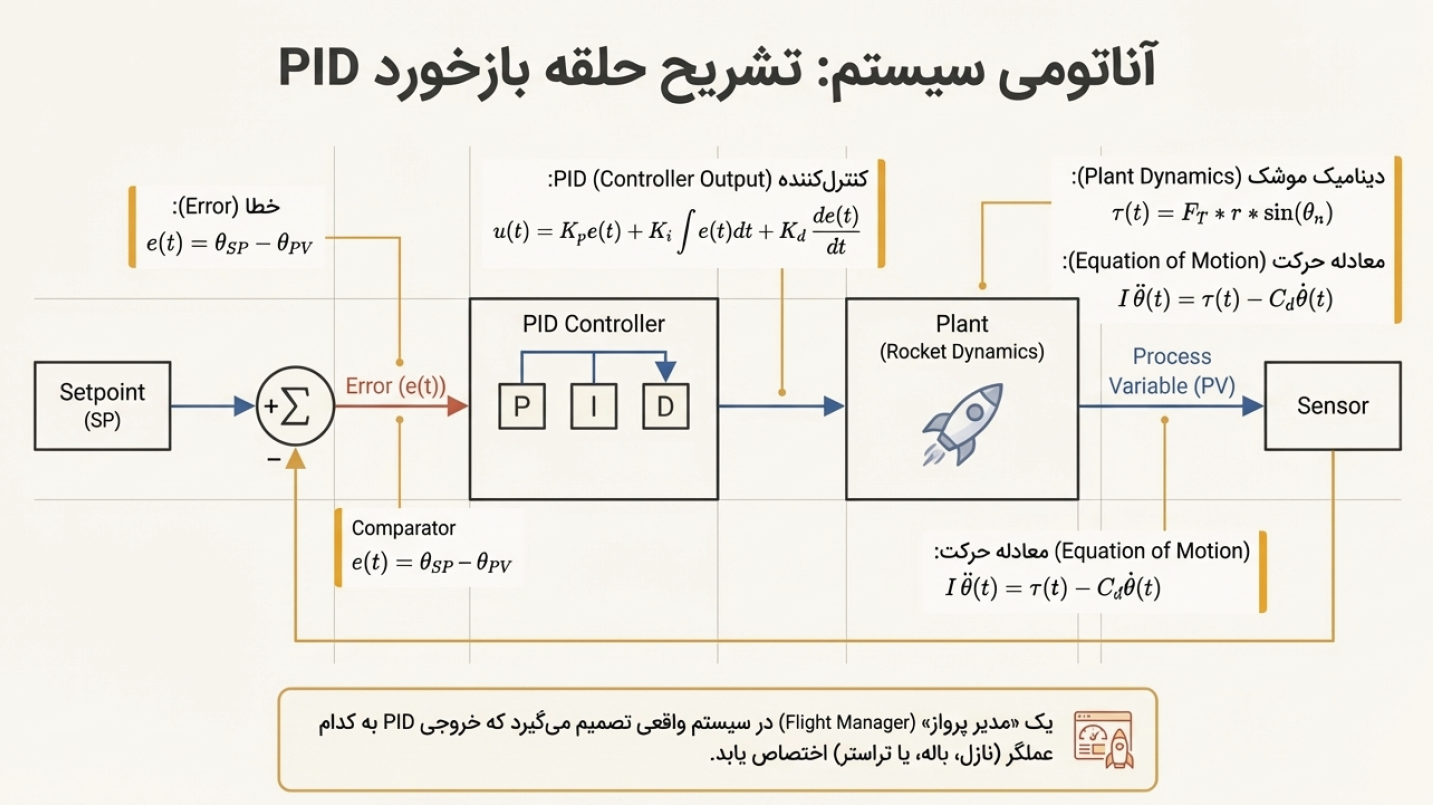
اکنون که با سه «مغز» P، I و D آشنا شدیم، ببینیم این اجزا چگونه در کامپیوتر پرواز (Flight Computer) با هم همکاری میکنند. این فرآیند، یک **«حلقه بازخورد» (Feedback Loop)** بیوقفه است که صدها یا هزاران بار در ثانیه اجرا میشود تا موشک را دقیقاً روی مسیر نگه دارد.
دیاگرام زیر، جزئیات کامل این حلقه و ارتباط آن با شبیهسازی ما را نشان میدهد:
# 🔄 تحلیل حلقهی بسته PID موشک
در این مدل حلقهی بسته از **Setpoint تا Sensor Feedback** امتداد دارد و ارتباط بین کنترلکننده PID و فیزیک موشک را بهصورت فرمولی نشان میدهد.
---
## 🔸 ورودی و مقایسهگر
**Setpoint (SP):**
$$
\theta_{\text{SP}} = \theta_{\text{desired}}
$$
**Process Variable (PV):**
$$
\theta_{\text{PV}} = \theta(t)
$$
**خطا:**
$$
e(t) = \theta_{\text{SP}} - \theta_{\text{PV}}
$$
---
## 🔸 کنترلکننده PID
در حوزهی زمان پیوسته:
$$
u(t) = K_p e(t) + K_i \int e(t)\,dt + K_d \frac{de(t)}{dt}
$$
خروجی کنترلکننده برابر است با:
$$
\theta_n(t) = u(t)
$$
---
## 🔸 دینامیک موشک (Plant)
گشتاور تولیدی:
$$
\tau(t) = F_T \, r \, \sin(\theta_n)
$$
معادله حرکت دورانی با اصطکاک زاویهای)
$$
I \ddot{\theta}(t) = \tau(t) - C_d \dot{\theta}(t)
$$
یا:
$$
\ddot{\theta} = \frac{F_T \, r \, \sin(\theta_n)}{I} - \frac{C_d}{I} \dot{\theta}
$$
## 🔸 معادلهی نهایی سیستم
این رابطه، رفتار کنترلی و فیزیکی موشک را در قالب یک سیستم حلقهبستهی کامل نمایش میدهد.
### نقش «مدیر پرواز» (Control Allocator)
دیاگرام بالا، یک حلقه PID را برای *یک* عملگر (مثل نازل) نشان میدهد. اما در یک موشک واقعی، یک لایه مدیریتی بالاتر به نام **«مدیر پرواز» (Flight Manager)** یا «تخصیصدهنده کنترل» (Control Allocator) وجود دارد.
این مدیر، خود یک PID *نیست*، بلکه یک تصمیمگیرنده است:
1. کنترلر اصلی (مثلاً `PID_Yaw` برای کنترل انحراف) میگوید: «من برای اصلاح مسیر به `۲۰-` واحد گشتاور نیاز دارم.»
2. «مدیر پرواز» این درخواست را دریافت میکند و بر اساس شرایط پرواز تصمیم میگیرد:
* **فاز ۱: سرعت کم (داخل اتمسفر):** «بالهها تقریباً بیاثرند. تمام `۲۰` واحد را به **PID نازل (TVC)** بده.»
* **فاز ۲: سرعت بالا (داخل اتمسفر):** «بالهها بسیار مؤثرند. `۱۵` واحد را به **PID بالهها** بده و `۵` واحد باقیمانده را به **PID نازل**.»
* **فاز ۳: خلاء (خارج از اتمسفر):** «بالهها کاملاً بیاثرند. تمام `۲۰` واحد را به **تراسترهای جانبی (RCS)** یا TVC بده.»
بنابراین، شبیهسازی ما در واقع در حال تنظیم یکی از این PIDهای تخصصی (PID نازل) است که تحت فرمان «مدیر پرواز» کار میکند.
## ۴. روش زیگلر-نیکولز (Ziegler-Nichols)
### الف) مقدمهای دقیق بر روش زیگلر-نیکولز (Ziegler-Nichols)
**مشکل:** ما میدانیم که به ضرایb `Kp`، `Ki` و `Kd` نیاز داریم. اما این اعداد را از کجا بیاوریم؟
* **حدس زدن:** انتخاب تصادفی این اعداد (مانند `Rocket 1, 2, 3` در تست قبلی) یک فرآیند آزمون و خطای بسیار طولانی، خستهکننده و غیرعلمی است.
* **ریاضیات محض:** محاسبه دقیق این ضرایb با استفاده از «توابع تبدیل» (Transfer Functions) و «تبدیل لاپلاس» (Laplace Transform) نیازمند داشتن یک مدل ریاضی کامل و بینقص از فیزیک موشک است که در دنیای واقعی تقریباً غیرممکن است.
**راهحل هوشمندانه:** روش زیگلر-نیکولز یک راهحل «تجربی» (Experimental) و هوشمندانه ارائه میدهد. این روش میگوید: «نیازی نیست فیزیک پیچیده سیستم را بدانید. کافیست سیستم را مانند یک "جعبه سیاه" در نظر بگیرید و یک آزمایش ساده روی آن انجام دهید تا "شخصیت" آن را کشف کنید.»
**منطق اصلی (The Core Idea):**
منطق زیگلر-نیکولز این است که «نقطه بحرانی» هر سیستم، همهچیز را درباره آن فاش میکند. این نقطه بحرانی، **مرز دقیق بین پایداری و ناپایداری** است.
1. اگر سیستم «پایدار» (Stable) باشد، نوسانهای آن میمیرند (مانند `Rocket 2` و `3`).
2. اگر سیستم «ناپایدار» (Unstable) باشد، نوسانهای آن تا بینهایت رشد میکنند (موشک متلاشی میشود).
3. اما یک نقطه «جادویی» در این بین وجود دارد: **«نوسان پایدار» (Sustained Oscillation)**.
در این نقطه، سیستم مانند یک آونگ ساعت، با دامنهای ثابت تا ابد نوسان میکند. این حالت به ما **«اثر انگشت» (Fingerprint)** سیستم را میدهد. زیگلر و نیکولز کشف کردند که اگر این اثر انگشت را پیدا کنیم، میتوانیم یک «دستور پخت» (Recipe) ثابت برای محاسبه هر سه ضریب PID ارائه دهیم.
#### فرآیند گام به گام زیگلر-نیکولز {#فرآیند-گام-به-گام-زیگلر-نیکولز}
این روش دقیقاً همان فرآیندی است که ما در شبیهسازی خود برای پیدا کردن `Kp = 0.006` طی کردیم:
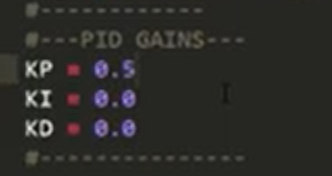
**گام ۱: آمادهسازی آزمایش (فقط P)**
* کنترلر را به سادهترین حالت خود در میآوریم. ما «حافظه گذشته» (I) و «ترمز آیندهنگر» (D) را خاموش میکنیم.
* `Ki = 0`
* `Kd = 0`
**گام ۲: پیدا کردن بهره نهایی ($K_u$)**
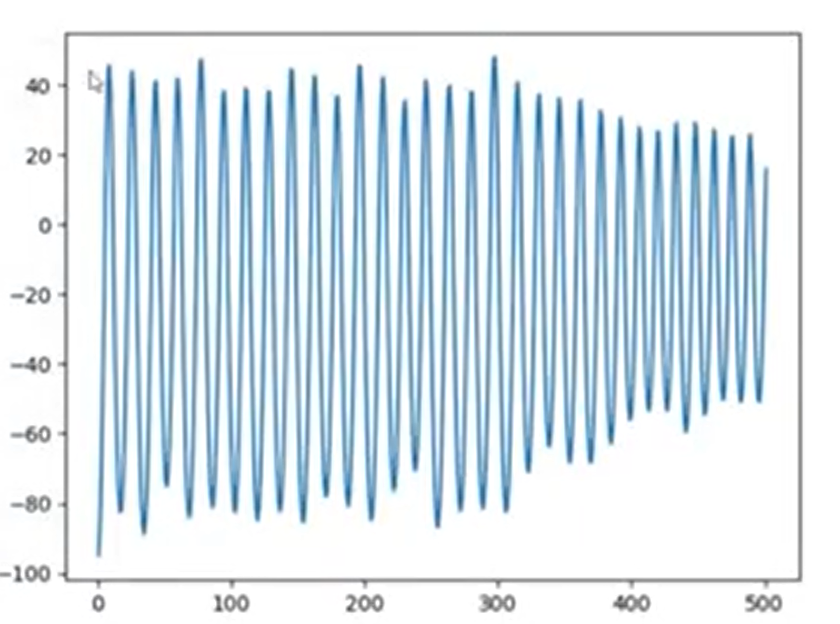
* ما شروع به افزایش پله پله `Kp` میکنیم و در هر مرحله به سیستم یک «ضربه» (خطای اولیه، مانند `Start Angle = 45`) وارد میکنیم.
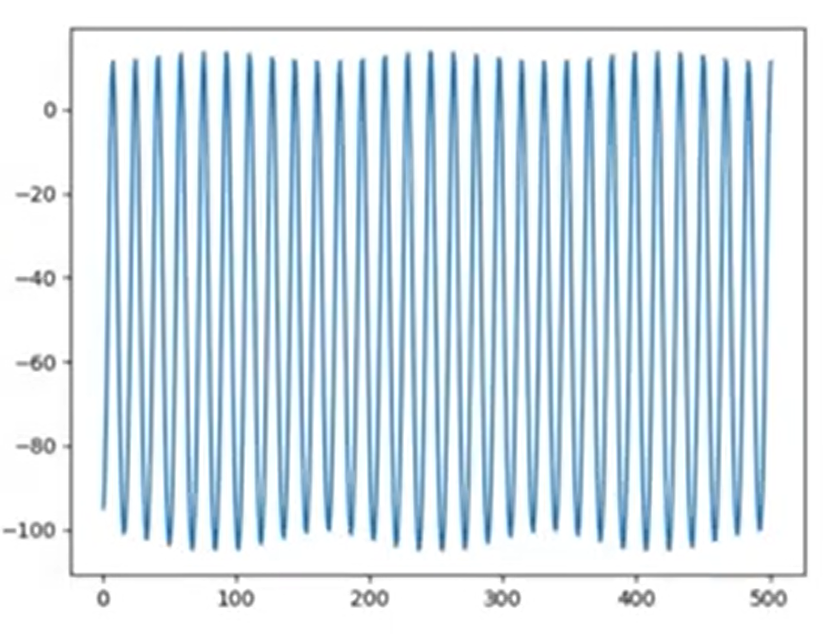
حالا خروجی ما این شکل نوسانی است
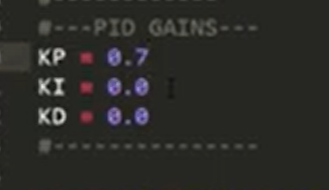
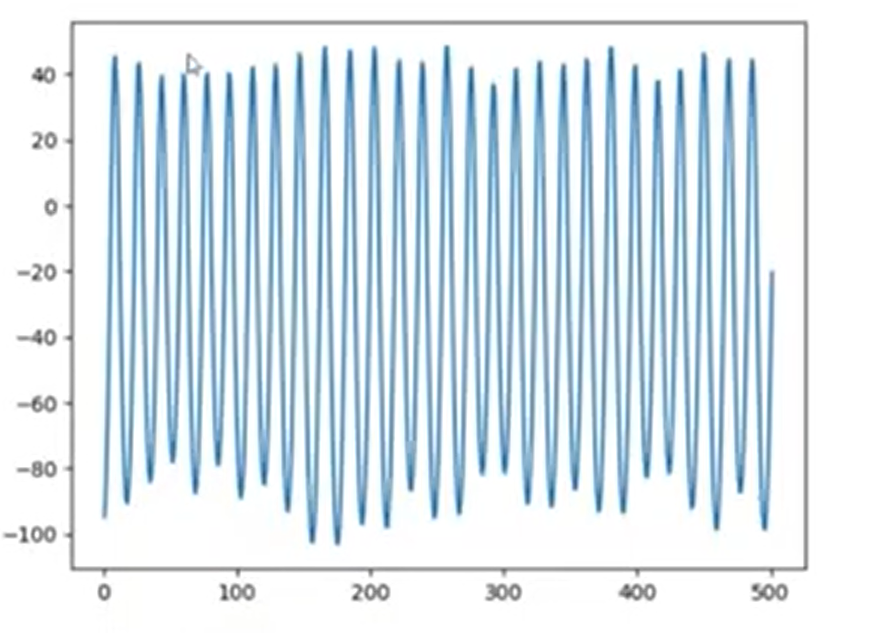
مقدار kp رو 2 برابر میکنیم
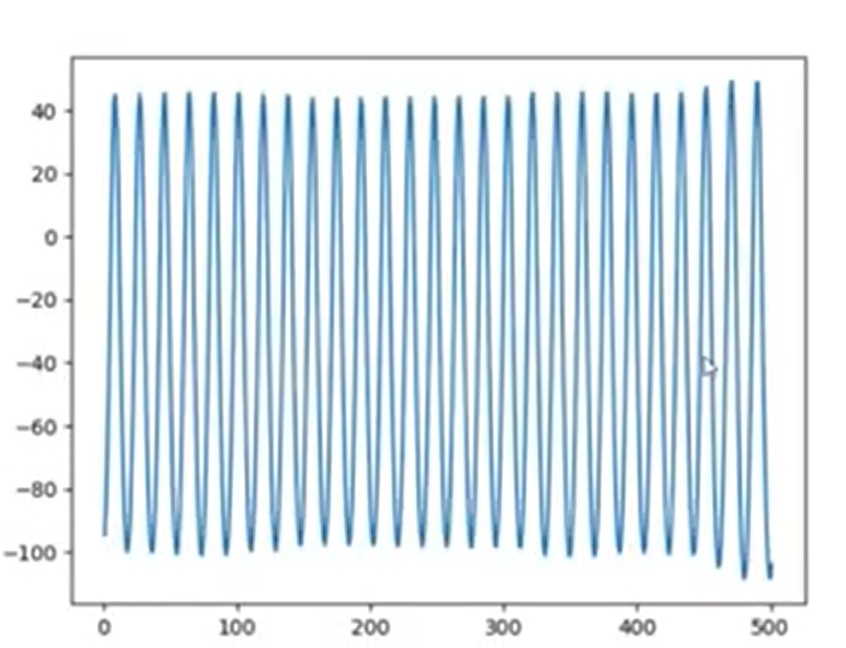
خروجی تست جدید :
همچنان خروجی نوسانی داریم
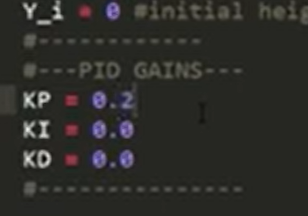
افزایش مقدار میدهیم :
خروجی تست جدید :
همونطر که میبنید نتیجه تست جدید خروجی میرا و مایل به صفر به ما میده
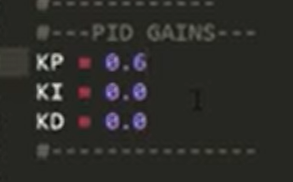
پس کمی از مقدار کم میکنیم تا به خروجی نوسان پایدار برسیم
خروجی تست جدید :
همونطور که میبینید ما نقطه بحرانی مدار رو پیدا کردیم
نوسان پایدار
ku=0.6
**گام ۳: پیدا کردن دوره نهایی ($T_u$)**
* در همان نمودار نوسان پایدار، با یک کرنومتر (یا با نگاه کردن به محور زمان)، مدت زمان یک نوسان کامل (مثلاً فاصله زمانی بین دو قله موج) را اندازهگیری میکنیم.
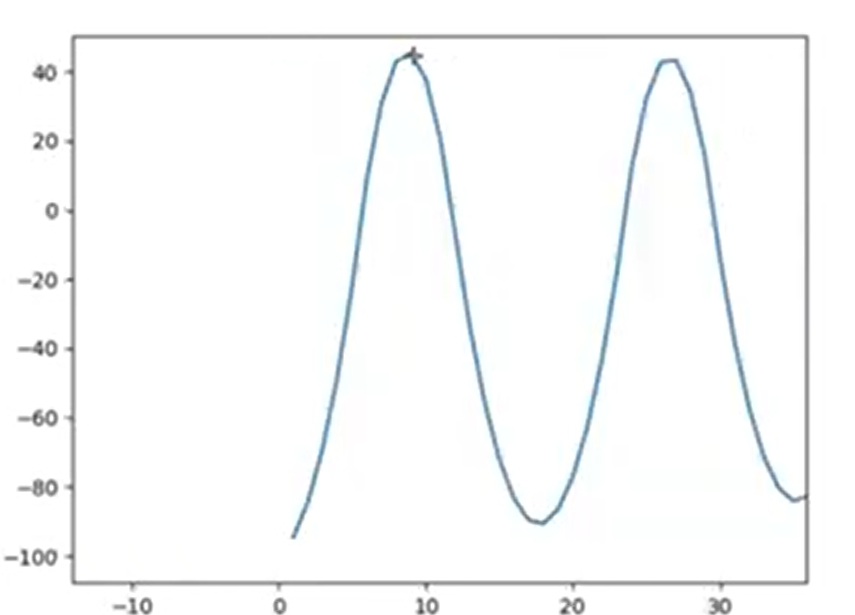
* این زمان را **«دوره نهایی» (Ultimate Period)** مینامیم و آن را **$T_u$** یادداشت میکنیم.
tu=18ms
**گام ۴: استفاده از دستور پخت (جدول زیگلر-نیکولز)**
حالا که دو عدد طلایی ($K_u$ و $T_u$) را داریم، از جدول استاندارد زیر برای محاسبه ضرایb نهایی استفاده میکنیم:
| نوع کنترلر | $K_p$ (ضریب تناسبی) | $T_i$ (زمان انتگرال) | $T_d$ (زمان مشتق) |
| :-------------------- | :------------------ | :------------------- | :---------------- |
| **PID (کلاسیک)** | **$0.6 \cdot K_u$** | **$T_u / 2$** | **$T_u / 8$** |
| PI (اگر D نخواهیم) | $0.45 \cdot K_u$ | $T_u / 1.2$ | - |
| P (اگر I و D نخواهیم) | $0.5 \cdot K_u$ | - | - |
**گام ۵: محاسبه ضرایb نهایی ($K_i$ و $K_d$)**
مهم است که توجه کنیم جدول بالا به ما $K_i$ و $K_d$ را مستقیماً نمیدهد، بلکه $T_i$ (زمان انتگرال) و $T_d$ (زمان مشتق) را میدهد. ما ضرایb نهایی را برای استفاده در کد خود اینگونه محاسبه میکنیم:
* $K_p = 0.6 \cdot K_u$=0.36
* $K_i = K_p / T_i$ (یا $K_i = 1.2 \cdot K_u / T_u$) = ki=40
* $K_d = K_p \cdot T_d$ (یا $K_d = 0.075 \cdot K_u \cdot T_u$)=kd=0.008
## ۵. شبیهسازی: درک عملی ضرایب PID
اکنون که تئوری PID و روش تنظیم (Tuning) آن را بررسی کردیم، زمان آن رسیده که به آزمایشگاه شبیهسازی برویم. هدف ما در این بخش این است که به صورت بصری «حس» کنیم هر کدام از ضرایb **P**، **I** و **D** در عمل چه تأثیری بر رفتار موشک میگذارند.
ما چهار آزمایش طراحی کردهایم. ابتدا، سیستم «ایدئال» و تنظیمشدهی خود را بررسی میکنیم. سپس، در هر آزمایش، عمداً یکی از پارامترها را از حالت تعادل خارج میکنیم تا نقش دقیق آن را در سیستم بهتر درک کنیم.
---
### آزمایش ۱: سیستم متعادل
در این آزمایش مت یک سیستم متعادل که رابطه بین زائویه نازل موشک و زاویه حرکت موشک رو محاسبه میکنه برسی میکنیم ، ما از ضرایبی استفاده میکنیم که از طریق محاسبات زیگلر-نیکولز به دست آوردیم. این تنظیمات، «خط پایه» (Baseline) ما برای یک سیستم خوشرفتار و پایدار هستند.
* **پارامترها:**
* $K_p$ (تناسبی): **1**
* $K_d$ (مشتقی): **30**
* $K_i$ (انتگرالی): **0.001**
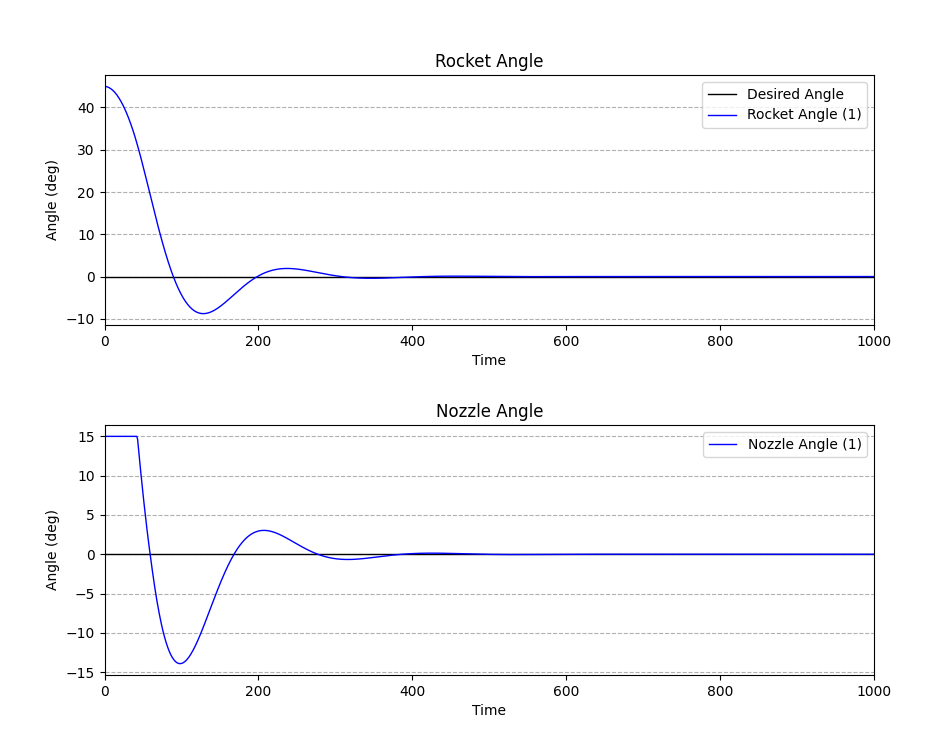
#### تحلیل (چه چیزی را مشاهده میکنیم؟)
بیایید با هم به دو نمودار نگاه کنیم. نمودار پایین (Nozzle Angle) «فرمان» کنترلر است و نمودار بالا (Rocket Angle) «پاسخ» موشک به آن فرمان است.
1. **واکنش اولیه (نمودار نازل):** در لحظه صفر، موشک خطای بزرگی (۴۵ درجه) دارد. کنترلر PID بلافاصله این خطا را تشخیص داده و با قدرت واکنش نشان میدهد. میبینیم که «زاویه نازل» فوراً به حداکثر مقدار خود (حدود ۱۳- درجه) میرسد تا موشک را در جهت مخالف هل دهد.
2. **اثر ترمز ( $K_d$ ):** همانطور که موشک به سرعت به سمت هدف (۰ درجه) برمیگردد، ترم $K_d$ (مشتقی) ما—که مقدار بالایی `30` دارد—نقش «ترمز» را ایفا میکند. این ترم میگوید: «سرعت نزدیک شدن به هدف زیاد است!» و شروع به کم کردن فرمان نازل میکند تا از عبور شدید از هدف (Overshoot) جلوگیری کند.
3. **نشست نهایی (Settling):** به لطف این هماهنگی، سیستم فقط یک «بیشجهش» (Overshoot) کوچک و کنترلشده تا حدود ۸- درجه را تجربه میکند. پس از آن، به سرعت نوسان را خنثی کرده و در زمانی کمتر از ۴۰۰ واحد، به آرامی روی زاویه ۰ درجه «مینشیند».
**نتیجه:** این یک پاسخ عالی است—سریع، دقیق و پایدار. حالا که میدانیم یک سیستم خوب چه شکلی است، بیایید در آزمایش بعدی ببینیم اگر $K_p$ را زیاد کنیم چه اتفاقی میافتد.
---
### آزمایش ۲: افزایش $K_p$ (سیستم تهاجمی) {#آزمایش-۲-افزایش-kp-سیستم-تهاجمی}
در این آزمایش، ما دو ضریب دیگر را ثابت نگه میداریم و فقط ضریب تناسبی ($K_p$) را از `1` به `5` افزایش میدهیم تا تأثیر آن را به تنهایی ببینیم.
* **پارامترها:**
* $K_p$ (تناسبی): **5** (از ۱ افزایش یافت)
* $K_d$ (مشتقی): **30** (ثابت)
* $K_i$ (انتگرالی): **0.001** (ثابت)
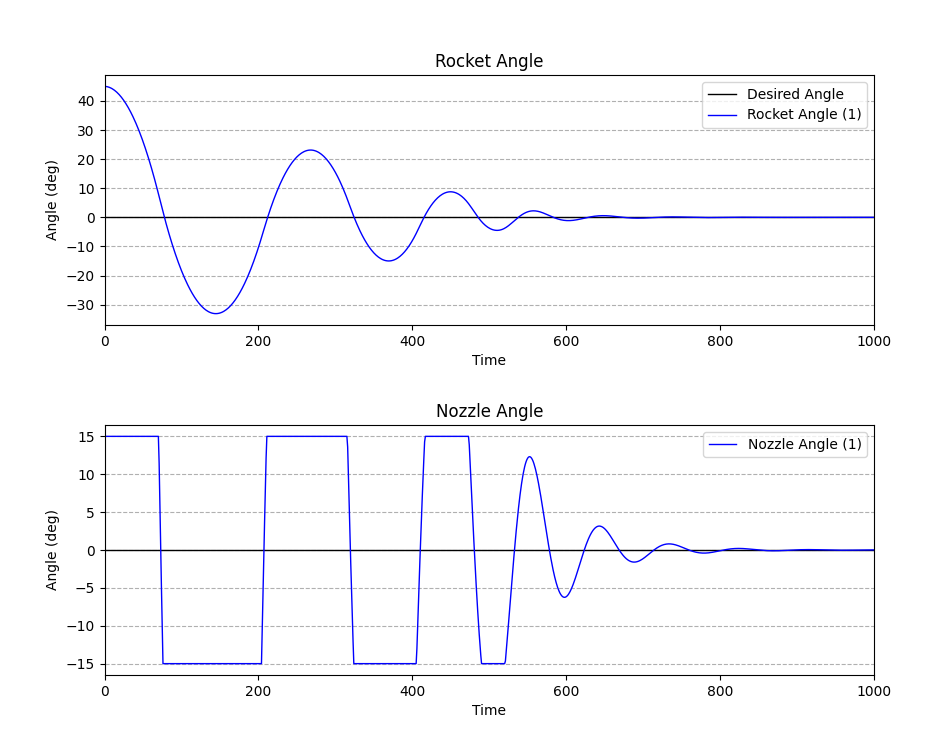
#### تحلیل (چه چیزی را مشاهده میکنیم؟)
1. **واکنش بسیار تهاجمی (نمودار نازل):** اولین چیزی که میبینیم این است که کنترلر بسیار «تهاجمی» یا «عصبی» شده است. به محض دیدن خطا، نازل (نمودار پایین) با تمام قدرت به یک سمت (`15-`) میچسبد.
2. **بیشجهش شدید (Overshoot):** این واکنش تهاجمی باعث میشود موشک (نمودار بالا) با سرعت بسیار زیادی به سمت صفر حرکت کند. اما $K_p$ آنقدر قوی است که «ترمز» $K_d$ دیگر حریف آن نمیشود. در نتیجه، موشک با شدت از هدف عبور کرده و یک «بیشجهش» (Overshoot) عظیم تا `32-` درجه را تجربه میکند (در حالی که در حالت متعادل فقط `8-` درجه بود).
3. **نوسان (Oscillation):** سیستم اکنون به شدت «کم-میرا» (Underdamped) است. کنترلر حالا خطای `32-` درجه را میبیند و دوباره با تمام قدرت در جهت مخالف (`15+`) فرمان میدهد. این فرمانهای «کوبشی» (از حدی به حد دیگر) باعث ایجاد یک نوسان شدید میشوند که چندین بار تکرار شده و زمان زیادی طول میکشد تا میرا شود (حدود ۸۰۰ واحد زمانی).
**نتیجه:** افزایش بیش از حد $K_p$، سیستم را سریعتر اما به شدت **ناپایدار و نوسانی** میکند. اگرچه سیستم در نهایت به تعادل میرسد، اما این سطح از نوسان در یک موشک واقعی، سوخت زیادی مصرف کرده و میتواند منجر به شکست سازهای شود.
---
### آزمایش ۳: حذف $K_d$ (سیستم بدون ترمز) {#آزمایش-۳-حذف-kd-سیستم-بدون-ترمز}
در این آزمایش، $K_p$ و $K_i$ را به حالت متعادل خود برمیگردانیم، اما این بار ضریب مشتقی ($K_d$) را از `30` به `1` کاهش میدهیم. این کار به معنای حذف کامل «ترمز» سیستم است.
* **پارامترها:**
* $K_p$ (تناسبی): **1** (ثابت)
* $K_d$ (مشتقی): **1** (از ۳۰ کاهش شدید یافت)
* $K_i$ (انتگرالی): **0.001** (ثابت)

#### تحلیل (چه چیزی را مشاهده میکنیم؟)
1. **فرمان «کوبشی» (Bang-Bang):** به نمودار پایین (Nozzle Angle) نگاه کنید. کنترلر دیگر هیچ «نرمی» ندارد. به محض اینکه موشک از خط صفر عبور میکند، فرمان نازل فوراً از حداکثر (`15+`) به حداقل (`15-`) میپرد. این رفتار شبیه همان کنترلر ساده «روشن/خاموش» است که در مقدمه گفتیم.
2. **نوسان پایدار (Unstable Oscillation):** نتیجه این فرمان کوبشی در نمودار بالا (Rocket Angle) کاملاً واضح است. سیستم *هرگز* به تعادل نمیرسد. موشک در یک چرخه نوسانی دائمی بین `45+` و `45-` درجه گیر کرده است.
3. **چرا این اتفاق افتاد؟** ما «آیندهنگر» یا «ترمز» سیستم را حذف کردیم. $K_p$ به تنهایی خطا را میبیند و فرمان جبران میدهد. اما وقتی موشک با سرعت به سمت صفر برمیگردد، $K_d$ (که اکنون `1` است) آنقدر ضعیف است که نمیتواند ترمز کند. موشک با تمام سرعت از هدف عبور میکند و باعث میشود $K_p$ دوباره در جهت مخالف فرمان دهد.
**نتیجه:** این آزمایش به وضوح نقش حیاتی ضریب **$K_d$** را در ایجاد **«پایداری» (Stability)** و **«میرایی» (Damping)** نشان میدهد. بدون یک $K_d$ به اندازه کافی قوی، کنترلر نمیتواند سرعت خود را پیشبینی یا کنترل کند و سیستم به یک نوسان دائمی و غیرقابل کنترل دچار میشود.
---
### آزمایش ۴: افزایش $K_i$ (اثر گلوله برفی) {#آزمایش-۴-افزایش-ki-اثر-گلوله-برفی}
در آخرین آزمایش، ما $K_p$ و $K_d$ را در حالت متعادل نگه میداریم، اما ضریب انتگرالی ($K_i$) را ۱۰۰ برابر افزایش میدهیم (از `0.001` به `0.1`). $K_i$ همان «حافظه گذشته» سیستم است و این آزمایش نشان میدهد که حافظه بیش از حد قوی چقدر میتواند مخرب باشد.
* **پارامترها:**
* $K_p$ (تناسبی): **1** (ثابت)
* $K_d$ (مشتقی): **30** (ثابت)
* $K_i$ (انتگرالی): **0.1** (از ۰.۰۰۱ به شدت افزایش یافت)
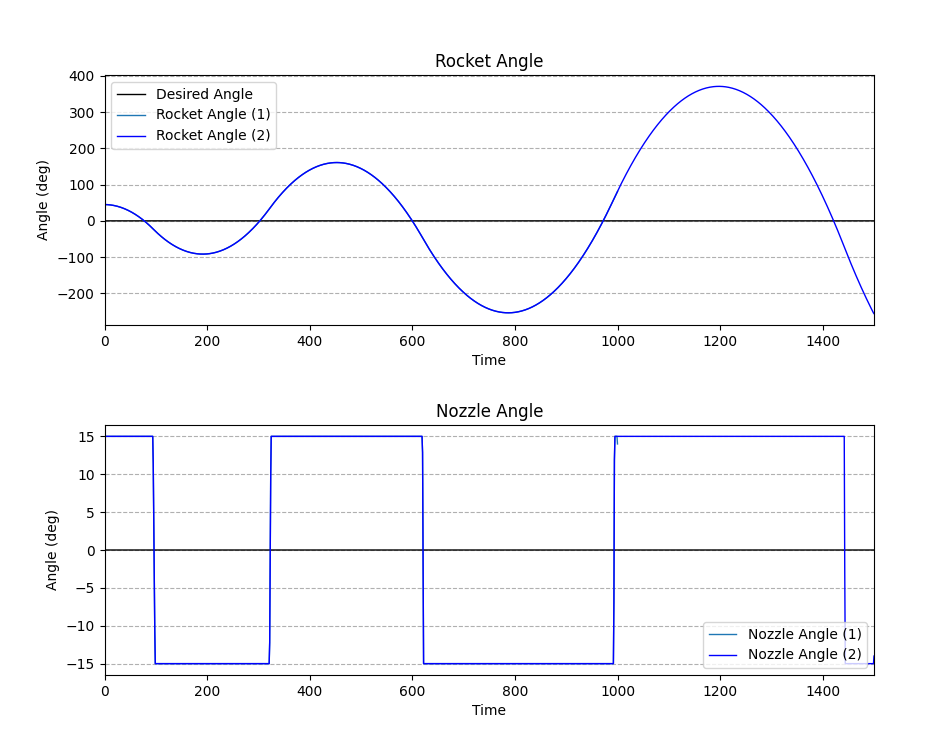
#### تحلیل (چه چیزی را مشاهده میکنیم؟)
1. **اثر گلوله برفی (Snowball Effect):** این نمودار یک شکست کامل را نشان میدهد. در حالی که $K_p$ و $K_d$ در تلاش برای اصلاح خطای اولیه ۴۵ درجه هستند، $K_i$ (که اکنون بسیار قوی است) شروع به «جمع کردن» آن خطای بزرگ میکند.
2. **«باد-آپ انتگرال» (Integral Windup):** مشکل اینجاست: حتی زمانی که موشک از خطای صفر عبور میکند، ترم $K_i$ آنقدر خطای گذشته را در خود «انباشته» کرده (مانند یک فنر کاملاً فشرده) که رها نمیکند. این نیروی انباشتهشده باعث یک «بیشجهش» (Overshoot) فاجعهبار تا حدود `100-` درجه میشود.
3. **ناپایداری فزاینده (Divergent Instability):** این فاجعه همینجا تمام نمیشود. کنترلر اکنون خطای جدید و بزرگتر (`100-` درجه) را میبیند و $K_i$ شروع به انباشتن این خطا در جهت مخالف میکند. این باعث یک بیشجهش *بزرگتر* در چرخه بعدی (تا `180+` درجه) و سپس `250-` درجه و... میشود. سیستم نه تنها نوسان میکند، بلکه نوسانات آن به صورت **فزاینده** در حال بدتر شدن است.
4. **فرمان اشباعشده (Saturated Command):** نمودار پایین (Nozzle Angle) نشان میدهد که کنترلر کاملاً از کنترل خارج شده و فقط فرمان را از حداکثر (`15+`) به حداقل (`15-`) میکوبد.
**نتیجه:** ضریب **$K_i$** برای از بین بردن خطاهای *کوچک و دائمی* بسیار حیاتی است، اما اگر بیش از حد قوی باشد، منجر به پدیده مخرب «Integral Windup» میشود. این پدیده مانند یک گلوله برفی، خطاها را بزرگ و بزرگتر کرده و سیستم را به طور کامل ناپایدار میکند. به همین دلیل است که $K_i$ در سیستم متعادل ما (آزمایش ۱) عددی بسیار کوچک (`0.001`) بود.
---
## ۶. نتیجهگیری نهایی: درسی که از شبیهسازی آموختیم {#۶-نتیجهگیری-نهایی-درسی-که-از-شبیهسازی-آموختیم}
این چهار آزمایش به وضوح نشان دادند که کنترل PID یک «بازی تعادل» (Balancing Act) است. هیچ ضریبی به تنهایی «بهترین» نیست؛ بلکه **«همسازی» (Harmony)** بین این سه ضریب است که یک سیستم پایدار میسازد.
ما به صورت عملی یاد گرفتیم که:
1. **$K_p$ (تناسبی):** «اسب کاری» سیستم است و واکنش اصلی را فراهم میکند. اگر $K_p$ بیش از حد زیاد باشد (آزمایش ۲)، سیستم «تهاجمی» و نوسانی میشود.
2. **$K_d$ (مشتقی):** «ترمز» و «پایدارکننده» سیستم است. اگر $K_d$ بیش از حد کم باشد (آزمایش ۳)، سیستم «ترمز» خود را از دست میدهد و وارد یک نوسان دائمی و غیرقابل کنترل میشود.
3. **$K_i$ (انتگرالی):** «تنظیمکننده دقیق» سیستم است. اگر $K_i$ بیش از حد زیاد باشد (آزمایش ۴)، «اثر گلوله برفی» ایجاد کرده و سیستم را به سمت ناپایداری فزاینده سوق میدهد.
درس نهایی: سیستم متعادل ما (آزمایش ۱) به این دلیل موفق بود که تعادل کاملی داشت: $K_p$ به اندازه کافی قوی بود تا سریع واکنش نشان دهد، $K_d$ به اندازه کافی قوی بود تا جلوی نوسان آن را بگیرد، و $K_i$ به اندازه کافی ضعیف بود که فقط خطاهای کوچک را بدون ایجاد «باد-آپ» برطرف کند.
منابع مورد استفاده: