کتابچه آموزشی فازورها

فصل اول: مقدمه‌ای بر سیگنال‌های سینوسی و نیاز به فازورها

۱. مقدمه

در تحلیل مدارهای جریان متناوب (AC)، سیگنال‌های سینوسی نقش بنیادینی دارند. تقریباً تمام پدیده‌های الکتریکی، از ولتاژ شبکه برق گرفته تا امواج رادیویی و صوتی، به صورت سینوسی قابل توصیف‌اند.
اما تحلیل مستقیم این سیگنال‌ها در حوزه زمان به‌دلیل وجود مشتق‌ها و انتگرال‌های متناوب، فرآیندی پیچیده است.
برای حل این مشکل، مفهوم فازور (Phasor) معرفی شد تا با تبدیل روابط سینوسی زمان‌محور به روابط جبری ساده‌تر در حوزه‌ی مختلط، تحلیل مدارها آسان‌تر شود.

۲. تعریف سیگنال سینوسی

سیگنال سینوسی تابعی از زمان است که به صورت زیر بیان می‌شود:

\[v(t) = V_m \sin(\omega t + \phi)\]

که در آن:

$ V_m $: دامنه یا بیشینه‌ی موج
$ \omega $: فرکانس زاویه‌ای بر حسب رادیان بر ثانیه
$ \phi $: زاویه‌ی فاز اولیه
$ t $: زمان

این تابع نمایانگر تغییر ولتاژ (یا جریان) در طول زمان است و رفتار تناوبی دارد.

نمایش یک موج سینوسی با دامنه و فاز مشخص

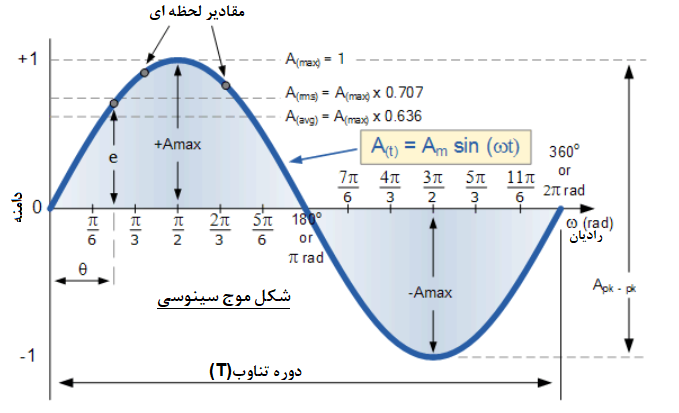
۳. مؤلفه‌های اصلی موج سینوسی

۱. دامنه (Amplitude): حداکثر مقدار سیگنال است و میزان انرژی یا شدت آن را نشان می‌دهد.
۲. فرکانس (Frequency): تعداد چرخه‌های کامل در واحد زمان است که برحسب هرتز (Hz) اندازه‌گیری می‌شود.
۳. فاز (Phase): موقعیت لحظه‌ای موج نسبت به مبدا زمان است و اختلاف زمانی یا زاویه‌ای بین دو سیگنال را نشان می‌دهد.

اختلاف فاز بین دو موج سینوسی می‌تواند باعث تداخل سازنده یا ویرانگر شود، که در تحلیل مدارها تأثیر مهمی دارد.

۴. مشکل تحلیل مستقیم در حوزه زمان

تحلیل یک مدار AC با منابع سینوسی به‌صورت مستقیم در حوزه زمان معمولاً نیازمند حل معادلات دیفرانسیل است.
برای مثال، در مدار زیر اگر منبع ولتاژ سینوسی به مقاومت و خازن متصل باشد، رابطه‌ی ولتاژ و جریان به صورت زیر است:

\[v(t) = Ri(t) + \frac{1}{C} \int i(t) \, dt\]

حل این معادله برای هر سیگنال ورودی سینوسی نیازمند محاسبات پیچیده است.

۵. ایده‌ی فازور و ساده‌سازی تحلیل

برای سادگی محاسبات، به‌جای تحلیل تابعی از زمان، از نمایش فازوری استفاده می‌شود.
در روش فازوری، سیگنال سینوسی با فرکانس ثابت به‌صورت یک عدد مختلط نمایش داده می‌شود:

\[V = V_m \angle \phi\]

یا در قالب نمایی:

\[V = V_m e^{j\phi}\]

در این نمایش، فقط دامنه و فاز نگهداری می‌شود و وابستگی به زمان حذف می‌گردد.
در نتیجه، روابط دیفرانسیلی به روابط جبری ساده تبدیل می‌شوند.

۶. ارتباط بین فازور و سیگنال زمان

با استفاده از تبدیل زیر می‌توان بین نمایش فازوری و نمایش زمانی جابجا شد:

\[v(t) = \Re \{\tilde{V} e^{j\omega t} \} = |{V}| \cos(\omega t + \phi)\]

که در آن $ \Re $ بخش حقیقی عدد مختلط را نشان می‌دهد.
به این ترتیب، فازورها ابزار قدرتمندی برای تحلیل مدارهای خطی با سیگنال‌های سینوسی هم‌فرکانس فراهم می‌کنند.

فصل دوم: تعریف و مفهوم فازور

در فصل پیش با سیگنال‌های سینوسی و نیاز به روشی ساده‌تر برای تحلیل آن‌ها آشنا شدیم.
در این فصل، مفهوم فازور (Phasor) را به عنوان ابزاری ریاضی و تصویری معرفی می‌کنیم که تحلیل مدارهای جریان متناوب را به شکل قابل توجهی ساده می‌سازد.

فازور به ما اجازه می‌دهد تا سیگنال‌های سینوسی را به کمک اعداد مختلط نمایش دهیم و محاسبات مربوط به فاز و دامنه را تنها با عملیات جبری انجام دهیم.
این روش در مباحث تحلیل مدار، کنترل، مخابرات و سیستم‌های سیگنالی بسیار پرکاربرد است.

۱. تعریف فازور

سیگنال سینوسی عمومی به صورت زیر بیان می‌شود:

\[x(t) = X_m \cos(\omega t + \phi)\]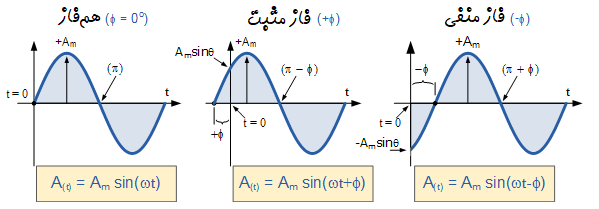

اگر این سیگنال فرکانس زاویه‌ای ثابت $ \omega $ داشته باشد، می‌توان آن را به یک عدد مختلط با دامنه و زاویه مشخص تبدیل کرد.
این عدد مختلط همان فازور است و به صورت زیر تعریف می‌شود:

\[\tilde{X} = X_m e^{j\phi}\]

در اینجا:

$ X_m $: دامنه‌ی سیگنال
$ \phi $: زاویه‌ی فاز (برحسب رادیان)
$ j $ : واحد موهومی با خاصیت $ j^2 = -1 $

بنابراین فازور فقط حاوی دامنه و فاز سیگنال است و وابستگی زمانی $ t $ حذف می‌شود.

۲. ارتباط بین فازور و تابع زمان

برای بازیابی سیگنال زمانی از فازور، کافی است فازور را در جمله‌ی زمانی $ e^{j\omega t} $ ضرب کرده و بخش حقیقی آن را در نظر بگیریم:

\[x(t) = \Re \{ \tilde{X} e^{j\omega t} \}\]

به این ترتیب، فازور نمایش فشرده‌ای از سیگنال سینوسی در حوزه‌ی مختلط است و می‌تواند رفتار زمانی موج را به‌صورت ضمنی نمایش دهد.

۳. نمایش فازور در صفحه مختلط

در صفحه مختلط (Complex Plane)، محور افقی بخش حقیقی و محور عمودی بخش موهومی را نشان می‌دهد.
هر فازور به‌صورت یک بردار با اندازه‌ی $ X_m $ و زاویه‌ی $ \phi $ از مبدا نمایش داده می‌شود.
به طور کلی، فازورها بردارهایی هستند که یک نقطه ابتدایی دارند و به آن «نقطه مبدأ» (Point of Origin) گفته می‌شود. نقطه انتهایی فازور، نمایانگر مقدار متغیر است و در جهت خلاف حرکت عقربه‌های ساعت با سرعتی برابر با فرکانس زاویه‌ای $ \omega $ فازور می‌چرخد. بنابراین به طور قراردادی فرض می‌شود که چرخش بردار در جهت خلاف عقربه‌های ساعت، فاز بردار را افزایش می‌دهد. گفته می‌شود که این چرخش، یک «چرخش مثبت» (Positive Rotation) است. به همین ترتیب، چرخش بردار در جهت عقربه‌های ساعت را «چرخش منفی» (Negative Rotation) می‌نامند. در شکل زیر دیاگرام فازور و نمایش لحظه‌ای آن، نشان داده شده است:

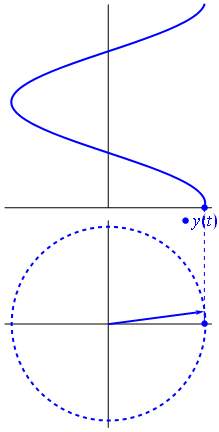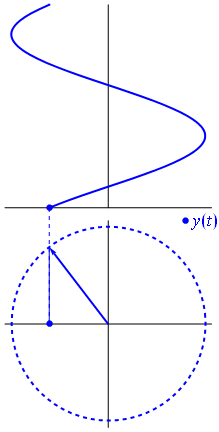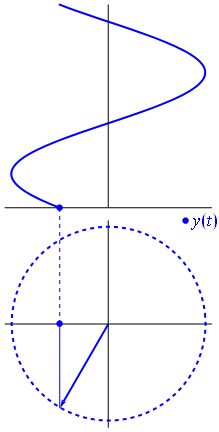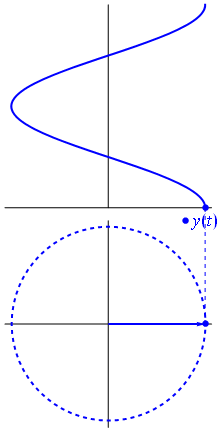
۴. نمایش قطبی و دکارتی فازور:

۴.۱ نمایش قطبی (Polar Form)

$\tilde{X} = X_m \angle \phi$

که در آن زاویه فاز برحسب درجه یا رادیان بیان می‌شود.

۴.۲ نمایش دکارتی (Rectangular Form)

$\tilde{X} = X_m (\cos \phi + j \sin \phi)$

بین این دو فرم، تبدیل‌ها به‌صورت زیر است:

\[\begin{cases} X_{re} = X_m \cos \phi \\ X_{im} = X_m \sin \phi \end{cases}\]

و در جهت معکوس:

\[\begin{cases} X_m = \sqrt{X_{re}^2 + X_{im}^2} \\ \phi = \tan^{-1}\left(\frac{X_{im}}{X_{re}}\right) \end{cases}\]

این روابط مبنای تمام محاسبات فازوری هستند.

۵. مثال کاربردی

فرض کنید سیگنال ولتاژ به صورت زیر است: $v(t) = 10\cos(\omega t + 30^\circ)$

نمایش فازوری آن برابر است با:

\[\tilde{V} = 10 \angle 30^\circ\]

اگر سیگنال جریان مدار نیز برابر باشد با:

\[i(t) = 5\cos(\omega t - 10^\circ)\]

آنگاه فازور متناظر جریان:

\[\tilde{I} = 5 \angle (-10^\circ)\]

اختلاف فاز بین ولتاژ و جریان برابر $ 40^\circ $ خواهد بود.
این اختلاف فاز مبنای محاسبه‌ی توان اکتیو و راکتیو در مدارهای AC است.

فصل سوم: نمایش ریاضی فازورها

در فصل قبل با مفهوم فازور و نحوه‌ی تعریف آن از یک سیگنال سینوسی آشنا شدیم.
اکنون نوبت آن است که با نمایش‌های مختلف ریاضی فازورها آشنا شویم و یاد بگیریم چگونه بین این نمایش‌ها تبدیل انجام دهیم.

فازورها در حقیقت اعداد مختلطی هستند که هم اندازه (دامنه) و هم زاویه (فاز) را در خود جای می‌دهند.
این ویژگی آن‌ها را به ابزار بسیار قدرتمندی برای تحلیل سیستم‌های سینوسی در حوزه‌ی فرکانس تبدیل کرده است.

۱. نمایش مختلط یک فازور

یک فازور را می‌توان به صورت عددی در صفحه مختلط نمایش داد.
اگر فازور $\tilde{X}$ دارای دامنه $X_m$ و زاویه فاز $\phi$ باشد، آن را می‌توان به شکل‌های مختلف زیر بیان کرد:

۱.۱ نمایش نمایی (Exponential Form)

$\tilde{X} = X_m e^{j\phi}$

۱.۱ نمایش قطبی (Polar Form)

$\tilde{X} = X_m \angle \phi$

۱.۳ نمایش دکارتی (Rectangular Form)

$\tilde{X} = X_{re} + jX_{im}$

که در آن: $\begin{cases} X_{re} = X_m \cos \phi \\ X_{im} = X_m \sin \phi \end{cases}$

این سه نمایش از نظر فیزیکی معادل‌اند و تنها تفاوت در روش نوشتن آن‌هاست.

۲. روابط بین نمایش‌ها

تبدیل بین نمایش‌های مختلف فازورها به کمک روابط هندسی ساده انجام می‌شود.
از روابط مثلثاتی می‌توان به‌راحتی به فرمول‌های زیر رسید:

۲.۱ از دکارتی به قطبی:

$X_m = \sqrt{X_{re}^2 + X_{im}^2}$ $\phi = \tan^{-1}\left(\frac{X_{im}}{X_{re}}\right)$

۲.۲ از قطبی به دکارتی:

$\begin{cases} X_{re} = X_m \cos \phi \\ X_{im} = X_m \sin \phi \end{cases}$

۳. تفسیر هندسی

در صفحه مختلط، فازور $\tilde{X}$ را می‌توان به صورت برداری از مبدا مختصات با زاویه‌ی $\phi$ نسبت به محور حقیقی نمایش داد.
طول این بردار اندازه‌ی فازور و جهت آن زاویه‌ی فاز را نشان می‌دهد.

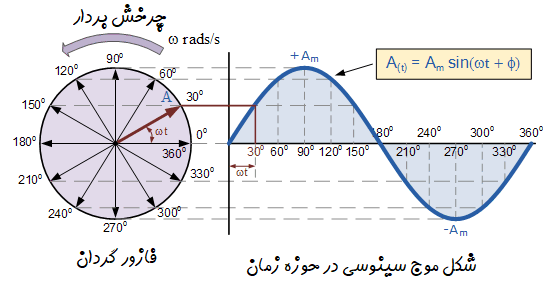
نمایش فازور در صفحه مختلط — طول بردار نشان‌دهنده دامنه و زاویه آن بیانگر فاز سیگنال است.

چرخش این بردار با سرعت زاویه‌ای $ \omega $ متناظر با نوسان سینوسی در حوزه‌ی زمان است.
اما در تحلیل فازوری، فرض می‌شود بردار ثابت است و تنها دامنه و زاویه‌ی آن بررسی می‌شود.

فصل چهارم: عملیات ریاضی روی فازورها

در فصل قبل یاد گرفتیم که فازورها را می‌توان در فرم‌های مختلف ریاضی مانند دکارتی، قطبی و نمایی نمایش داد.
اکنون در این فصل، نحوه‌ی انجام عملیات ریاضی روی فازورها را بررسی می‌کنیم.
این عملیات شامل جمع، تفریق، ضرب و تقسیم است که در تحلیل مدارهای AC به‌طور گسترده به کار می‌روند.

۱. اختلاف فاز بین دو موج سینوسی

فرض کنید اختلاف فاز دو شکل موج سینوسی به صورت زیر باشد:

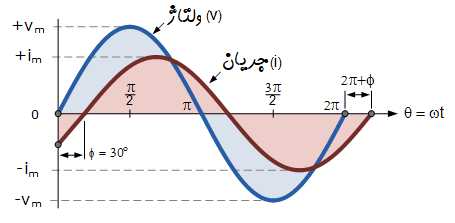
عبارت عمومی ریاضی برای تعریف این دو کمیت سینوسی به صورت زیر نوشته می‌شود: $v(t) = V_m\sin(\omega t)$ $i(t) = I_m\sin(\omega t - \phi)$

جریان $ i $، نسبت به ولتاژ $ v $، به اندازهٔ زاویهٔ $ \phi $ تأخیر دارد.
در این مثال، این اختلاف فاز برابر با $ 30^\circ $ است.
اختلاف بین دو فازور که نشان‌دهندهٔ دو کمیت سینوسی هستند، با زاویهٔ $ \phi $ نشان داده می‌شود.
این دو موج سینوسی در شکل زیر نشان داده شده‌اند:

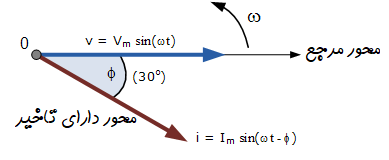
دیاگرام فازور نشان داده شده مربوط به زمان صفر $ (t = 0) $ روی محور افقی است.
طول فازورها متناسب با مقدار ولتاژ $ V $ و جریان $ I $ در لحظهٔ صفر است.
گفته می‌شود که فازور جریان نسبت به فازور ولتاژ، به اندازهٔ زاویهٔ $ \phi $ تأخیر دارد.
دو فازور در جهت خلاف حرکت عقربه‌های ساعت دوران می‌کنند،
پس زاویهٔ $ \phi $ نیز در خلاف جهت عقربه‌های ساعت اندازه‌گیری می‌شود.

اگر دو موج را در زمان $ t = 30^\circ $ نگه داریم، دیاگرام فازور مربوطه مانند شکل زیر خواهد شد:

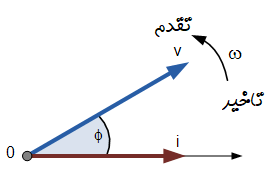
بار دیگر مشاهده می‌شود که فازور جریان نسبت به فازور ولتاژ تاخیر دارد، زیرا دو شکل موج فرکانس یکسانی دارند.

در لحظه‌ای که شکل موج جریان در محور افقی از نقطه صفر عبور می‌کند، می‌توان این لحظه از زمان را به عنوان مرجع جدید فازور جریان در نظر گرفت. بنابراین می‌توان گفت که فازور ولتاژ نسبت به فازور جریان به اندازه زاویه $\phi$,«تقدم» دارد. در هر حال، یک فازور به عنوان «فازور مرجع» در نظر گرفته می‌شود و بقیه فازورها نسبت به این مرجع، تقدم یا تاخیر دارند.

۲. جمع و تفریق فازورها

جمع دو فازور

در برخی موارد (مثلا در مدارهای سری AC، که مولفه‌ها با یکدیگر هم‌فاز نیستند)، لازم است دو شکل موج متناوب سینوسی با یکدیگر جمع شود. اگر مولفه‌ها هم‌فاز باشند (یعنی هیچ اختلاف فازی بین دو کمیت وجود نداشته باشد)، می‌توان مثل حالت DC، دو بردار را به صورت جبری جمع کرد. برای مثال، اگر دو ولتاژ ۵۰ ولت و ۲۵ ولت با یکدیگر، هم‌فاز باشند، برآیند این دو بردار، برابر ۷۵ ولت خواهد شد. اگر دو موج هم‌فاز نباشند (یعنی بردارهای آنها جهت یا نقاط شروع متفاوتی داشته باشد)، باید هنگام جمع دو فازور زاویه بین آن دو را در نظر گرفت. فازور نتیجه یا بردار برآیند، با استفاده از «قانون متوازی‌الاضلاع» محاسبه می‌شود. شکل زیر، دو شکل موج AC را نشان می‌دهد:

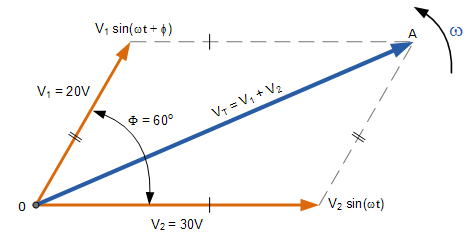
در این شکل دو فازور یکی $ V_1 $ با اندازهٔ ماکزیمم ۲۰ ولت و دیگری $ V_2 $ با اندازهٔ ماکزیمم ۳۰ ولت نشان داده شده است.
فرض می‌شود که فاز $ V_2 $ از $ V_1 $ به اندازهٔ $ 60^\circ $ تقدم دارد.
ولتاژ کلی $ V_T $ را می‌توان با رسم دیاگرام فازور و سپس رسم متوازی‌الاضلاع محاسبه کرد.
دو ضلع این متوازی‌الاضلاع، ولتاژهای $ V_1 $ و $ V_2 $ هستند.
به این ترتیب، مجموع دو فازور به‌راحتی با اندازه‌گیری طول قطر متوازی‌الاضلاع محاسبه می‌شود.
به این قطر، بردار برآیند (Resultant Vector) نیز گفته می‌شود.
نقطهٔ ضعف این روش آن است که رسم دو فازور و مقایسه‌بندی آن‌ها زمان‌بر است.
شکل زیر، دیاگرام برآیند دو فازور و نمایش لحظه‌ای برآیند را نشان می‌دهد:

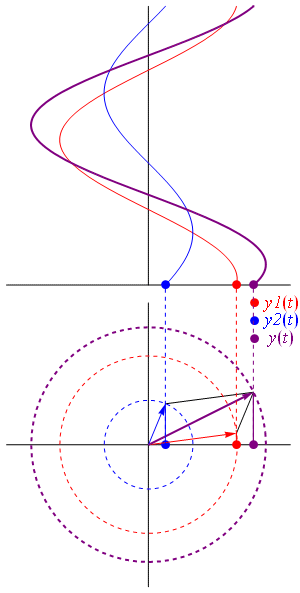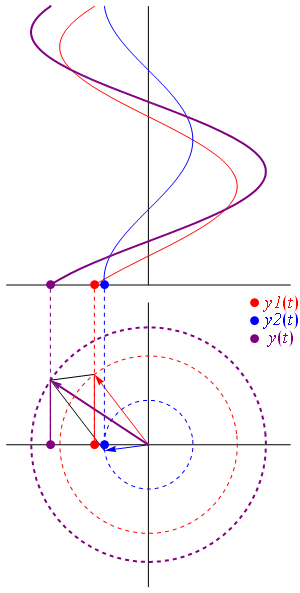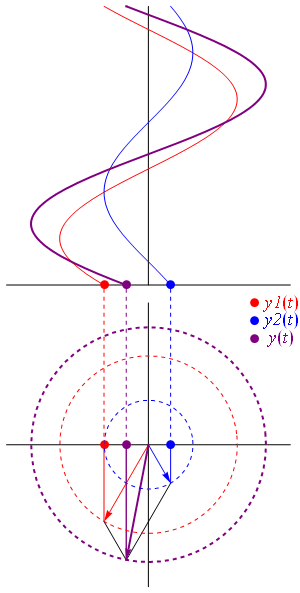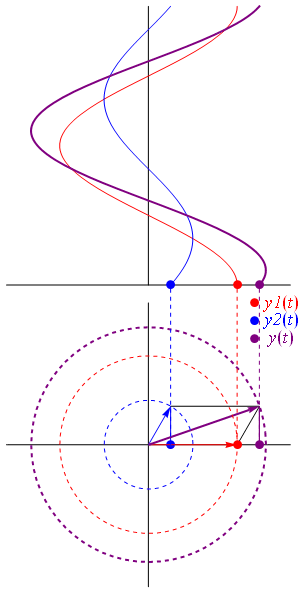
تفریق برداری دو فازور

تفریق دو فازور بسیار شبیه به روش متوازی الاضلاع است با این تفاوت که اختلاف دو بردار، قطر دیگر متوازی‌الاضلاع به دست آمده از دو بردار $V_1$ و $V_2$ است که در شکل زیر نشان داده شده است:

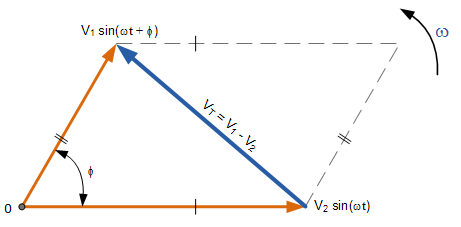
پس به طور خلاصه: برای جمع و تفریق فازورها، مناسب‌ترین فرم، فرم دکارتی (Rectangular) است، زیرا در این حالت مؤلفه‌های حقیقی و موهومی را می‌توان مستقیماً با هم جمع یا تفریق کرد.

اگر دو فازور داشته باشیم:

$\tilde{A} = A_{re} + jA_{im}$ $\tilde{B} = B_{re} + jB_{im}$

آنگاه:

\[\tilde{A} + \tilde{B} = (A_{re} + B_{re}) + j(A_{im} + B_{im})\] \[\tilde{A} - \tilde{B} = (A_{re} - B_{re}) + j(A_{im} - B_{im})\]

مثال عددی

دو فازور زیر را در نظر بگیرید:

$\tilde{A} = 4 + j3$ $\tilde{B} = 2 - j1$

جمع و تفریق آن‌ها برابر است با:

\[\tilde{A} + \tilde{B} = (4+2) + j(3-1) = 6 + j2\] \[\tilde{A} - \tilde{B} = (4-2) + j(3 - (-1)) = 2 + j4\]

اگر بخواهیم نتیجه را به فرم قطبی بنویسیم:

$|\tilde{A} + \tilde{B}| = \sqrt{6^2 + 2^2} = 6.32$ $\angle (\tilde{A} + \tilde{B}) = \tan^{-1}\left(\frac{2}{6}\right) = 18.4^\circ$

۳. ضرب فازورها

برای ضرب دو فازور، مناسب‌ترین فرم فرم قطبی (Polar) است، چون در این حالت، تنها کافی است اندازه‌ها را در هم ضرب کنیم و زاویه‌ها را جمع کنیم.

اگر داشته باشیم:

$\tilde{A} = A_m \angle \alpha$ $\tilde{B} = B_m \angle \beta$

آنگاه:

\[\tilde{A} \times \tilde{B} = (A_m B_m) \angle (\alpha + \beta)\]

مثال عددی

اگر:

$\tilde{A} = 5 \angle 20^\circ$ $\tilde{B} = 3 \angle -40^\circ$

آنگاه:

\[\tilde{A} \times \tilde{B} = 15 \angle (-20^\circ)\]

یعنی اندازه‌ها ضرب می‌شوند و زاویه‌ها جمع می‌گردند.

۴. تقسیم فازورها

برای تقسیم دو فازور نیز فرم قطبی مناسب است. در این حالت، اندازه‌ها بر هم تقسیم و زاویه‌ها از هم تفریق می‌شوند:

\[\frac{\tilde{A}}{\tilde{B}} = \left(\frac{A_m}{B_m}\right) \angle (\alpha - \beta)\]

مثال عددی

اگر:

\[\tilde{A} = 12 \angle 70^\circ, \quad \tilde{B} = 4 \angle 10^\circ\]

آنگاه:

\[\frac{\tilde{A}}{\tilde{B}} = 3 \angle (60^\circ)\]

۵. خواص جبری فازورها

فازورها از قواعد معمولی جمع، ضرب و توزیع در اعداد مختلط پیروی می‌کنند.
مهم‌ترین خواص عبارت‌اند از:

جابجایی (Commutative): $\tilde{A} + \tilde{B} = \tilde{B} + \tilde{A}$
ترکیبی (Associative): $(\tilde{A} + \tilde{B}) + \tilde{C} = \tilde{A} + (\tilde{B} + \tilde{C})$
توزیعی (Distributive): $\tilde{A}(\tilde{B} + \tilde{C}) = \tilde{A}\tilde{B} + \tilde{A}\tilde{C}$

این قوانین باعث می‌شوند محاسبات در حوزه‌ی فازوری مشابه محاسبات جبری معمولی باشد.

۶. دیاگرام فازور سه فاز

در مثال‌های قبل، تنها به شکل موج‌های تک فاز AC اشاره شد. به عنوان مثالی از موج تک فاز می‌توان یک سیم‌پیچ چرخان در میدان مغناطیسی را در نظر گرفت. اما اگر سه سیم‌پیچ مشابه در نظر گرفته شود که هر کدام تعداد برابر دور دارند و در زوایای الکتریکی ۱۲۰ درجه نسبت به هم روی شفت یک روتور قرار گرفته‌اند، یک ولتاژ سه فاز ایجاد خواهد شد. ولتاژ سه فاز متعادل از سه ولتاژ سینوسی تشکیل شده است که همه آنها اندازه و فرکانس برابر دارند اما غیر هم‌فاز هستند و دقیقا به اندازه ۱۲۰ درجه اختلاف فاز دارند.

سه بردار با رنگ‌های قرمز، زرد و آبی را برای نشان دادن فاز هر یک از بردارها در نظر می‌گیریم. بردار قرمز رنگ به عنوان فاز مرجع فرض می‌شود. مانند فازورهای تک فاز اشاره شده در بالا، فازور سه فاز نیز چرخشی در جهت خلاف عقربه‌های ساعت نسبت به نقطه مبدأ دارد که با نماد $\omega$ با واحد رادیان بر ثانیه نشان داده می‌شود. فازورها برای یک سیستم متصل متعادل ستاره یا مثلث به صورت زیر نشان داده می‌شود:

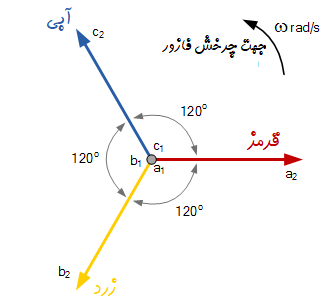
ولتاژ این سه فاز همگی مقداری برابر دارند، اما زاویهٔ فاز آن‌ها متفاوت است.
سه سیم‌پیچ به یکدیگر در نقاط $ a_1 $، $ b_1 $ و $ c_1 $ متصل شده‌اند.
این نقطه به‌عنوان زمین خنثی در نظر گرفته می‌شود.
اگر فازور قرمز را به‌عنوان مرجع فاز در نظر بگیریم، هر کدام از فازورها بر اساس نقطهٔ مشترک زمین تعریف می‌شود.

اگر فازور قرمز $ V_{RN} $ را به‌عنوان ولتاژ مرجع در نظر بگیریم، می‌توان گفت فازور زرد $ (V_{YN}) $ به اندازهٔ ۱۲۰ درجه از $ V_{RN} $ تأخیر دارد.
به همین ترتیب، فازور آبی $ (V_{BN}) $ از فازور زرد رنگ، به اندازهٔ ۱۲۰ درجه تأخیر دارد.
همچنین می‌توان گفت که $ V_{BN} $ نسبت به فازور قرمز رنگ $ (V_{RN}) $ به اندازهٔ ۱۲۰ درجه تقدم دارد.

بنابراین می‌توان معادلات ولتاژ سه فاز را به‌صورت زیر نوشت:

\[V_{RN} = V_m \sin(\theta) \quad \text{فازور قرمز}\] \[V_{YN} = V_m \sin(\theta - 120^\circ) \quad \text{فازور زرد}\] \[V_{BN} = V_m \sin(\theta - 240^\circ) = V_m \sin(\theta + 120^\circ) \quad \text{فازور آبی}\]

از آن‌جا که سه فازور نسبت به هم ۱۲۰ درجه اختلاف دارند، می‌توان گفت دیاگرام فازور شکل بالا، متعادل است.
در یک سیستم سه‌فاز متعادل، جمع فازورها برابر صفر است، یعنی:

\[V_{a} + V_{b} + V_{c} = 0\]

نکته مهم: فازورها و فرکانس ثابت

عملیات فازوری فقط زمانی معتبر است که سیگنال‌های سینوسی در مدار هم‌فرکانس باشند.
اگر فرکانس‌ها متفاوت باشند، دیگر نمی‌توان از جمع یا ضرب فازوری استفاده کرد و باید تحلیل در حوزه‌ی زمان انجام شود.

فصل پنجم: کاربرد فازورها در تحلیل مدارهای AC

در فصل‌های پیشین با مفهوم فازور و عملیات ریاضی مرتبط با آن آشنا شدیم.
در این فصل، از فازورها برای تحلیل مدارهای جریان متناوب (AC Circuits) استفاده می‌کنیم.
هدف اصلی این است که روش‌های پایه‌ای مانند قانون اهم، قانون کیرشهف و تحلیل امپدانس را در حوزه فازوری بررسی کنیم.

تحلیل فازوری به ما اجازه می‌دهد تا:

به‌جای حل معادلات دیفرانسیل در حوزه‌ی زمان، از معادلات جبری ساده در حوزه‌ی فازور استفاده کنیم.

۱. تبدیل عناصر مدار به حوزه فازور

برای تحلیل مدارها در حوزه فازور، ابتدا باید هر عنصر مدار را (مقاومت، سلف، خازن) به مدل امپدانسی (Impedance Model) آن تبدیل کنیم.

الف) مقاومت (Resistor)

در مقاومت، ولتاژ و جریان هم‌فازند:

$v(t) = V_m \cos(\omega t + \theta)$ $i(t) = I_m \cos(\omega t + \theta)$

بنابراین در حوزه فازور:

\[\tilde{V} = R \tilde{I}\]

و امپدانس مقاومت برابر است با:

\[Z_R = R\]

ب) سلف (Inductor)

در سلف، ولتاژ از جریان ۹۰ درجه پیش‌فاز است.
در حوزه زمان:

\[v(t) = L \frac{di(t)}{dt}\]

با تبدیل فازوری:

\[\tilde{V} = j \omega L \tilde{I}\]

در نتیجه امپدانس سلف برابر است با:

\[Z_L = j \omega L\]

ج) خازن (Capacitor)

در خازن، جریان از ولتاژ پیش‌فاز است (۹۰ درجه زودتر):

\[i(t) = C \frac{dv(t)}{dt}\]

با تبدیل فازوری:

\[\tilde{I} = j \omega C \tilde{V}\]

و بنابراین:

\[Z_C = \frac{1}{j \omega C} = -j \frac{1}{\omega C}\]

۲. قانون اهم در حوزه فازور

قانون اهم در حوزه فازور به سادگی رابطه زیر است:

\[\tilde{V} = \tilde{I} Z\]

که در آن $ Z $ می‌تواند شامل ترکیبی از مقاومت، سلف و خازن باشد.

مثال ساده

اگر مداری شامل یک مقاومت $ R = 10Ω $ و یک سلف $ L = 0.1H $ به فرکانس $ f = 50Hz $ باشد و جریان آن به‌صورت زیر تعریف شود:

\[i(t) = 2\cos(100\pi t) \, A\]

امپدانس معادل مدار برابر است با:

\[Z = R + j\omega L = 10 + j(2\pi \times 50 \times 0.1) = 10 + j31.4\]

دامنه ولتاژ فازوری:

\[|\tilde{V}| = |\tilde{I}|\times|Z| = 2 \times \sqrt{10^2 + 31.4^2} = 65.4 \, V\]

و زاویه فاز ولتاژ:

\[\theta_V = \tan^{-1}\left(\frac{31.4}{10}\right) = 72.5^\circ\]

بنابراین فازور ولتاژ:

\[\tilde{V} = 65.4 \angle 72.5^\circ\]

۳. قوانین کیرشهف در حوزه فازور

قوانین KCL (قانون جریان کیرشهف) و KVL (قانون ولتاژ کیرشهف) به همان صورت در حوزه فازور نیز معتبرند، با این تفاوت که مقادیر ولتاژ و جریان به‌صورت فازوری بیان می‌شوند.

KCL: مجموع جریان‌های ورودی به یک گره برابر مجموع جریان‌های خروجی است: $\sum \tilde{I}_{in} = \sum \tilde{I}_{out}$
KVL: مجموع ولتاژها در هر حلقه مدار برابر صفر است: $\sum \tilde{V} = 0$

۴. امپدانس معادل مدارهای ساده

برای مدارهای متوالی (سری):

\[Z_{eq} = Z_1 + Z_2 + \dots + Z_n\]

برای مدارهای موازی:

\[\frac{1}{Z_{eq}} = \frac{1}{Z_1} + \frac{1}{Z_2} + \dots + \frac{1}{Z_n}\]

این روابط درست مانند مقاومت‌ها در حوزه DC هستند، با این تفاوت که $ Z $ عددی مختلط است.

۵. نمایش فازوری توان

توان در مدارهای AC شامل سه مؤلفه است:

توان اکتیو $ P $
توان راکتیو $ Q $
توان ظاهری $ S $

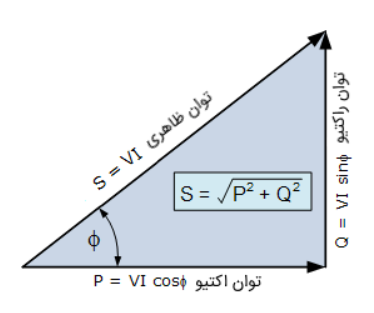
رابطه‌ی بین آن‌ها در قالب مثلث توان نشان داده می‌شود:

$S = P + jQ$ $|S| = V_{rms} I_{rms}^*$

زاویه‌ی فاز بین ولتاژ و جریان همان زاویه‌ی مثلث توان است.

۶. مزیت اصلی تحلیل فازوری

تحلیل فازوری باعث می‌شود:

معادلات دیفرانسیلی به معادلات جبری تبدیل شوند.
محاسبات با اعداد مختلط ساده شود.
روابط بین فاز، دامنه و فرکانس واضح‌تر دیده شوند.
تحلیل مدار در حالت ماندگار سینوسی بسیار سریع‌تر انجام گیرد.

حل مثال هایی از تحلیل مدار با استفاده از فازور

۱. اعداد مختلط در مدار RC

مثال: جریان را بر حسب ${t}$ در مدار زیر بیابید.

import schemdraw
import schemdraw.elements as elm

with schemdraw.Drawing() as d:
    elm.SourceSin().label('cos(t)').up()
    elm.Resistor().label('2Ω').right()
    elm.Capacitor().label('1F').down()
    elm.Line().left()

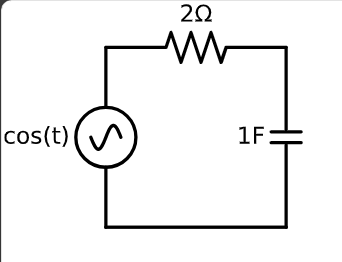
اول $\omega$ و $V_a$ را پیدا میکنیم: $V(t) = \cos t = 1 \angle 0^\circ$

از رابطه فوق، به دست می‌آید:

\[\Rightarrow V_A = 1 , \ \phi = 0^\circ , \ \omega = 1\]

حالا شکل مدار فازوری را رسم میکنیم

import schemdraw
import schemdraw.elements as elm

with schemdraw.Drawing() as d:
    elm.SourceSin().label('1 ∠ 0°').up()
    elm.Resistor().label('2Ω').right()
    elm.Capacitor().label('1/jw').down()
    elm.Line().left()

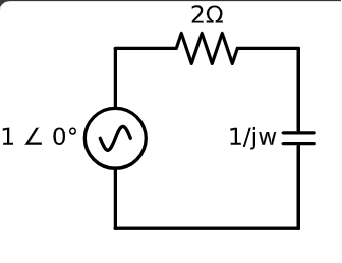
تعریف عدد موهومی

\[j = \sqrt{-1} \Rightarrow j^2 = -1\]

تبدیل عدد مختلط به قالب نمایی

$a + jb = \sqrt{a^2 + b^2} \angle \tan^{-1}\left(\frac{b}{a}\right)$

محاسبه جریان در مدار

\[I = \frac{V_A}{R + \frac{1}{j\omega}}\] \[\Rightarrow I = \frac{1}{2 + \frac{1}{j\omega}} = \frac{j\omega}{2j\omega + 1}\] \[\Rightarrow I = \frac{j}{2j + 1} \cdot \frac{1 - 2j}{1 - 2j} = \frac{j - 2j^2}{1 - 4j^2}\]

ساده‌سازی

$\Rightarrow I = \frac{j + 2}{5}$

تبدیل به قالب دامنه و فاز

\[\Rightarrow 2 + j = \sqrt{2^2 + 1^2} \angle \tan^{-1}\left(\frac{1}{2}\right) = \sqrt{5} \angle 26.5^\circ\] \[\Rightarrow I = \frac{\sqrt{5} \angle 26.5^\circ}{5} = \frac{\sqrt{5}}{5} \angle 26.5^\circ\]

شکل زمانی جریان

$\Rightarrow I(t) = \frac{\sqrt{5}}{5} \cos(t + 26.5^\circ)$ —

۲. اعداد مختلط در مدار RL

مثال: جریان را بر حسب ${t}$ در مدار زیر بیابید. $V_s = 3 \sin\left( 2t + \frac{\pi}{2} \right)$

import schemdraw
import schemdraw.elements as elm

with schemdraw.Drawing() as d:
    elm.SourceSin().label('Vs').up()
    elm.Resistor().label('2Ω').right()
    elm.Inductor().label('3H').down()
    elm.Line().left()

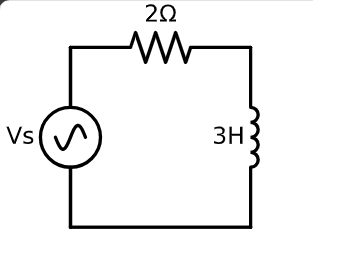
گام اول: یافتن ω و (V_A)

ابتدا رابطه‌ی عمومی عدد مختلط را می‌نویسیم:

\[z = r e^{j\theta} = r(\cos\theta + j\sin\theta)\]

برای ولتاژ ورودی داریم:

\[V_s = 3\sin\left(2t + \frac{\pi}{2}\right) = 3e^{j\frac{\pi}{2}}\]

که از آن نتیجه می‌شود:

$\Rightarrow V_A = 3 , \quad \phi = \frac{\pi}{2} , \quad \omega = 2$ حالا مدار فازوری را رسم میکنیم

import schemdraw
import schemdraw.elements as elm

with schemdraw.Drawing() as d:
    elm.SourceSin().label('3 ∠ 0°').up()
    elm.Resistor().label('2Ω').right()
    elm.Inductor().label('3jw').down()
    elm.Line().left()

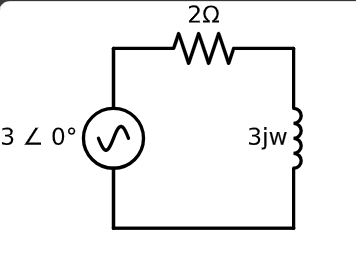
محاسبه جریان ( I ) در مدار R-L

فرمول پایه:

\[I = \frac{V_A}{R + L j \omega}\]

جایگذاری مقادیر:

\[\frac{3}{2 + 3 j \omega} = \frac{3}{2 + 6j}\]

ضرب مزدوج:

\[I = \frac{3}{2 + 6j} \cdot \frac{2 - 6j}{2 - 6j}\]

محاسبه صورت و مخرج:

\[I = \frac{3 \cdot 2 + 3(-6j)}{4 - 36j^2} = \frac{6 - 18j}{40} = \frac{3 - 9j}{20}\]

تبدیل به قالب دامنه و فاز:

\[3 - 9j = \sqrt{3^2 + (-9)^2} \angle \tan^{-1}\left(\frac{-9}{3}\right) = \sqrt{90} \angle -71.5^\circ\]

نتیجه:

\[I = \frac{\sqrt{90} \angle -71.5^\circ}{20}\]

شکل موج زمانی جریان:

\[I(t) = \frac{\sqrt{90}}{20} \sin(2t - 71.5^\circ)\]

فصل ششم: نتیجه‌گیری و منابع

۱. جمع‌بندی مفاهیم کلیدی

در طول این کتابچه، مسیر یادگیری از سیگنال‌های سینوسی ساده تا تحلیل پیشرفته‌ی مدارهای AC را با استفاده از مفهوم فازور (Phasor) طی کردیم.
مهم‌ترین دستاوردها را می‌توان به شکل زیر خلاصه کرد:

فازور ابزاری ریاضی است که بیانگر دامنه و فاز یک سیگنال سینوسی در قالب عدد مختلط است.
با تبدیل تابع زمانی به فازور، تحلیل مدار از حوزه‌ی زمان به حوزه‌ی فرکانس منتقل می‌شود.
عملیات پیچیده‌ی دیفرانسیلی در حوزه‌ی زمان، در حوزه‌ی فازور به عملیات جبری ساده تبدیل می‌گردد.
امپدانس (Impedance) مفهومی است که به کمک فازورها تعریف می‌شود و نقش مقاومت معادل را در مدارهای AC ایفا می‌کند.
قوانین اهم و کیرشهف در حوزه‌ی فازور نیز معتبرند و تحلیل مدار را بسیار ساده‌تر می‌سازند.
در سطح پیشرفته‌تر، فازورها زیرمجموعه‌ای از تحلیل‌های فرکانسی و لاپلاسی هستند و پایه‌ای برای فهم پاسخ فرکانسی، فیلترها و سیستم‌های دینامیکی محسوب می‌شوند.

۲. کاربردهای عملی فازورها

فازورها در بسیاری از زمینه‌های مهندسی و صنعتی کاربرد دارند:

تحلیل و طراحی مدارهای AC: شامل محاسبه جریان، ولتاژ و توان در مدارهای تک‌فاز و سه‌فاز.
سیستم‌های قدرت (Power Systems): برای تحلیل پایداری، تنظیم ولتاژ و تلفات در خطوط انتقال.
الکترونیک صنعتی: مانند درایو موتورهای AC و کنترل توان.
مخابرات: در تحلیل مدولاسیون و سیگنال‌های سینوسی حامل.
تحلیل سیگنال و سیستم: به عنوان مبنای درک تبدیل‌های فوریه و لاپلاس.

۳. آینده‌ی یادگیری

برای ادامه‌ی یادگیری در این حوزه پیشنهاد می‌شود:

مطالعه‌ی مفصل‌تر در مورد تبدیل لاپلاس و فوریه.
یادگیری نرم‌افزارهای تحلیل مدار مثل Multisim، LTSpice، و MATLAB Simulink.
تمرین تحلیل مدارهای پیچیده‌تر با استفاده از روش‌های ماتریسی (مانند روش نود و مش در حوزه‌ی فازور).
بررسی کاربرد فازورها در سیستم‌های سه‌فاز و تحلیل نامتقارن.

۴. سخن پایانی

فازورها تنها یک ابزار ریاضی نیستند؛ بلکه زبانی هستند که مهندسان برق با آن رفتار دنیای واقعی سیگنال‌ها و مدارهای AC را توصیف می‌کنند.
درک عمیق این مفهوم، پلی است میان تحلیل کلاسیک و درک سیستم‌های پیچیده‌تر در حوزه فرکانس.

📚 منابع و مراجع

در تهیه‌ی این کتابچه از منابع آموزشی معتبر زیر استفاده شده است:

Complex Numbers in Phasors — Circuit Electronics Student Effort
Introduction to Phasors — Circuit Electronics Student Effort
Phasor Analysis — Circuit Electronics Student Effort
Phasors 1 — Circuit Electronics Student Effort
Fourier and Laplace Analysis — Circuit Electronics Student Effort
MIT OpenCourseWare — Circuits and Electronics (6.002)
Dorf, R. C., & Svoboda, J. A. Introduction to Electric Circuits, 10th Edition, Wiley, 2020.
Alexander, C. K., & Sadiku, M. N. O. Fundamentals of Electric Circuits, 6th Edition, McGraw-Hill, 2017.

کتابچه آموزشی فازورها

Hadi Sadoghi Yazdi

کتابچه آموزشی فازورها

فصل اول: مقدمه‌ای بر سیگنال‌های سینوسی و نیاز به فازورها

۱. مقدمه

۲. تعریف سیگنال سینوسی

۳. مؤلفه‌های اصلی موج سینوسی

۴. مشکل تحلیل مستقیم در حوزه زمان

۵. ایده‌ی فازور و ساده‌سازی تحلیل

۶. ارتباط بین فازور و سیگنال زمان

فصل دوم: تعریف و مفهوم فازور

۱. تعریف فازور

۲. ارتباط بین فازور و تابع زمان

۳. نمایش فازور در صفحه مختلط

۴. نمایش قطبی و دکارتی فازور:

۴.۱ نمایش قطبی (Polar Form)

۴.۲ نمایش دکارتی (Rectangular Form)

۵. مثال کاربردی

فصل سوم: نمایش ریاضی فازورها

۱. نمایش مختلط یک فازور

۱.۱ نمایش نمایی (Exponential Form)

۱.۱ نمایش قطبی (Polar Form)

۱.۳ نمایش دکارتی (Rectangular Form)

۲. روابط بین نمایش‌ها

۲.۱ از دکارتی به قطبی:

۲.۲ از قطبی به دکارتی:

۳. تفسیر هندسی

فصل چهارم: عملیات ریاضی روی فازورها

۱. اختلاف فاز بین دو موج سینوسی

۲. جمع و تفریق فازورها

جمع دو فازور

تفریق برداری دو فازور

مثال عددی

۳. ضرب فازورها

مثال عددی

۴. تقسیم فازورها

مثال عددی

۵. خواص جبری فازورها

۶. دیاگرام فازور سه فاز

نکته مهم: فازورها و فرکانس ثابت

فصل پنجم: کاربرد فازورها در تحلیل مدارهای AC

۱. تبدیل عناصر مدار به حوزه فازور

الف) مقاومت (Resistor)

ب) سلف (Inductor)

ج) خازن (Capacitor)

۲. قانون اهم در حوزه فازور

مثال ساده

۳. قوانین کیرشهف در حوزه فازور

۴. امپدانس معادل مدارهای ساده

۵. نمایش فازوری توان

۶. مزیت اصلی تحلیل فازوری

حل مثال هایی از تحلیل مدار با استفاده از فازور

۱. اعداد مختلط در مدار RC

تعریف عدد موهومی

تبدیل عدد مختلط به قالب نمایی

محاسبه جریان در مدار

ساده‌سازی

تبدیل به قالب دامنه و فاز

شکل زمانی جریان

۲. اعداد مختلط در مدار RL

گام اول: یافتن ω و (V_A)

محاسبه جریان ( I ) در مدار R-L

فصل ششم: نتیجه‌گیری و منابع

۱. جمع‌بندی مفاهیم کلیدی

۲. کاربردهای عملی فازورها

۳. آینده‌ی یادگیری

۴. سخن پایانی

📚 منابع و مراجع

📬 راه‌های ارتباطی