تحلیل حساسیت در مدارات دیودی

تحلیل حساسیت در مدارات دیودی

اطلاعات نویسنده

نام: شقایق سادات رضوی عمرانی

1. مقدمه

تحلیل حساسیت بسیار مهم است، به‌ویژه در مهندسی برق و الکترونیک، چون مدارها همیشه دارای تلرانس هستند. هیچ المان الکتریکی کاملاً ایده‌آل نیست و هر عنصر در مدار همیشه یک محدوده مقادیر دارد.
مثال: یک مقاومت با تلرانس ۵٪ همیشه مقداری بین $R_\text{min}$ و $R_\text{max}$ خواهد داشت. حتی دقیق‌ترین المان‌ها هم تلرانس دارند. بنابراین درک حساسیت و کاربرد آن در تحلیل مدار ضروری است.

1.1 تحلیل حساسیت چیست؟

تحلیل حساسیت بررسی می‌کند که خروجی یک سیستم چقدر به تغییر کوچک در یک ورودی یا پارامتر وابسته است.

مثال: در مدار تقسیم‌کننده ولتاژ، تحلیل حساسیت به ما نشان می‌دهد که با تغییر مقادیر مقاومت‌ها، ولتاژ خروجی چگونه تغییر می‌کند.

به زبان ساده:

اگر یک تغییر کوچک در یک پارامتر منجر به تغییر کوچک در خروجی شود، حساسیت کم است.
اگر یک تغییر کوچک باعث تغییر بزرگ شود، حساسیت بالا است.

یا حتی ساده‌تر:

“اگر $x$ را به مقداری % تغییر دهم، $y$ به چه % تغییر خواهد کرد؟”

1.2 چرا از تحلیل حساسیت استفاده می‌کنیم؟

تحلیل حساسیت به بهینه‌سازی مدار کمک می‌کند:

1. شناسایی المان‌ها یا پارامترهای بحرانی که بیشترین تاثیر را روی عملکرد دارند.
2. کاهش اثرات تغییرات یا عدم قطعیت‌ها و بهبود قابلیت اطمینان مدار.
3. حذف المان‌ها یا پارامترهای غیرضروری و کاهش هزینه.

1.3 چگونه تحلیل حساسیت انجام دهیم؟

روش‌های مختلفی برای تحلیل حساسیت وجود دارد:

• تحلیل مقدار نامی: خروجی با مقادیر استاندارد المان‌ها محاسبه می‌شود و خط پایه برای مقایسه فراهم می‌کند.
• تحلیل بدترین حالت: با مقادیر حداقل و حداکثر المان‌ها محاسبه می‌شود تا کران بالا و پایین خروجی مشخص شود.
• تحلیل مونت کارلو: از مقادیر تصادفی المان‌ها بر اساس توزیع احتمال استفاده می‌کند و تحلیل آماری خروجی ارائه می‌دهد.

1.4 نمایش نتایج تحلیل حساسیت

نتایج را می‌توان به روش‌های زیر نمایش داد:

• ضرایب حساسیت: نشان می‌دهد خروجی نسبت به هر پارامتر چقدر تغییر می‌کند.
• نمودار حساسیت: نمایش گرافیکی تغییر خروجی با تغییر یک پارامتر.
  مثال: نمودار ولتاژ خروجی در مقابل مقدار مقاومت.
• هیستوگرام حساسیت: توزیع مقادیر خروجی را نشان می‌دهد.

1.5 محاسبه حساسیت

حساسیت $S$ یک متغیر $Y$ نسبت به یک پارامتر $X$ به صورت زیر تعریف می‌شود:

\[S = \frac{\Delta Y / Y}{\Delta X / X}\]

اگر تغییرات کوچک باشند، می‌توان از مشتق استفاده کرد:

\[S = \frac{dY}{dX} \cdot \frac{X}{Y}\]

این فرمول بدون بعد است و نشان می‌دهد که $Y$ چقدر به تغییرات $X$ حساس است.

1.6 تحلیل حساسیت در مدارها

تحلیل حساسیت مشخص می‌کند که چگونه تغییر یک پارامتر در ورودی مدار، خروجی را تغییر می‌دهد.
این تحلیل به ما کمک می‌کند تا بفهمیم طراحی مدار چقدر در برابر تلرانس المان‌ها مقاوم است و برای بهبود پایداری و دقت طراحی تصمیم‌گیری کنیم.

مقدمه تحلیل حساسیت در مدارات دیودی

مدارات دیودی یکی از پرکاربردترین و بنیادی‌ترین بخش‌های الکترونیک هستند که در گستره‌ی وسیعی از مدارهای عملی مانند یکسوسازها، تنظیم‌کننده‌های ولتاژ، محدودکننده‌ها (Clippers) و مدارات جبران‌سازی دما استفاده می‌شوند.
رفتار این مدارات به شدت به ویژگی‌های ذاتی دیود (مانند جریان اشباع، ولتاژ حرارتی و ضریب n) و همچنین به پارامترهای خارجی نظیر ولتاژ منبع، مقاومت‌های مدار و دمای محیط وابسته است.

از آنجا که در عمل، هیچ‌کدام از این پارامترها ثابت و ایده‌آل نیستند (به دلیل وجود تلرانس قطعات، تغییرات دما و نوسانات منبع تغذیه)، ممکن است عملکرد مدار نسبت به شرایط طراحی اولیه تغییر کند.
به عنوان مثال، در یک مدار یکسوساز ساده، تغییر چند درجه‌ای دمای محیط می‌تواند باعث تغییر قابل‌توجهی در ولتاژ خروجی شود. این تغییرات ممکن است در کاربردهای حساس، منجر به خطا یا حتی خرابی مدار گردد.

در چنین شرایطی، تحلیل حساسیت (Sensitivity Analysis) به‌عنوان یک ابزار مهندسی بسیار مؤثر برای درک میزان تأثیر تغییرات پارامترهای مختلف بر عملکرد مدار مورد استفاده قرار می‌گیرد.
با استفاده از این تحلیل، می‌توان مشخص کرد که کدام پارامترها تأثیر بیشتری بر خروجی دارند و در نتیجه، با کنترل آن‌ها یا طراحی مناسب، پایداری عملکرد مدار را افزایش داد.

اهمیت تحلیل حساسیت تنها به شناخت تأثیرات محدود نمی‌شود، بلکه در فرآیند بهینه‌سازی طراحی نیز نقش اساسی دارد. به کمک آن می‌توان:

• نقاط بحرانی طراحی را شناسایی کرد؛
• از قطعات با تلرانس مناسب‌تر استفاده نمود؛
• و در نهایت مدارهایی با عملکرد پایدارتر و قابل اعتمادتر طراحی کرد.

در این پروژه، هدف آن است که با استفاده از روش‌های تحلیلی و شبیه‌سازی، تأثیر تغییرات پارامترهای مختلف بر رفتار مدارهای دیودی مورد بررسی قرار گیرد.
ابتدا مفاهیم پایه‌ای تحلیل حساسیت و روابط ریاضی مربوط به آن توضیح داده می‌شود؛ سپس در مدارهای مختلف دیودی (دیود ساده و یکسوساز نیم‌موج) این تحلیل به‌صورت عددی و گرافیکی انجام خواهد شد.
در پایان نیز نتایج به‌دست‌آمده مورد مقایسه، تحلیل و ارائه‌ی راهکارهای طراحی برای کاهش حساسیت مدارها قرار خواهند گرفت.

2. مبانی تئوری تحلیل حساسیت در مدارات دیودی

2.1 تعریف تحلیل حساسیت (Sensitivity Analysis)

تحلیل حساسیت (Sensitivity Analysis) شاخه‌ای از تحلیل مهندسی است که بررسی می‌کند چگونه تغییرات کوچک در پارامترهای ورودی مدار (مانند مقاومت، منبع ولتاژ یا دما) باعث تغییر در متغیرهای خروجی (مثل جریان، ولتاژ یا توان) می‌شود.

به بیان ساده‌تر:

تحلیل حساسیت مشخص می‌کند کدام پارامترها بیشترین تأثیر را بر عملکرد مدار دارند.

در طراحی مدارهای عملی، هیچ قطعه‌ای دقیق و بدون تلرانس نیست — بنابراین تحلیل حساسیت کمک می‌کند تا پایداری مدار در برابر تغییرات پارامترها تضمین شود.

2.2 مفهوم کلی حساسیت

فرض کنید خروجی مدار تابعی از چند پارامتر ورودی باشد:

\[y = f(p_1, p_2, p_3, \dots, p_n)\]

اگر یکی از پارامترها، مثلاً $p_i $، اندکی تغییر کند، خروجی نیز تغییر می‌کند.
در این حالت، حساسیت خروجی نسبت به پارامتر $p_i$ به صورت زیر تعریف می‌شود:

\[S_{p_i}^y = \frac{\partial y}{\partial p_i}\]

این رابطه، میزان تغییر مطلق خروجی را بر اثر تغییر کوچک در پارامتر نشان می‌دهد.

2.3 انواع حساسیت

تحلیل حساسیت معمولاً در دو حالت بیان می‌شود:

2.3.1 حساسیت مطلق (Absolute Sensitivity)

در این حالت، میزان تغییر خروجی نسبت به تغییر پارامتر، بدون نرمال‌سازی بررسی می‌شود:

\[S_{p}^{y} = \frac{\partial y}{\partial p}\]

کاربرد: وقتی مقدار واقعی تغییرات مهم است (مثلاً در جریان‌های بالا یا ولتاژهای دقیق).
مثال: اگر در یک مدار دیودی، ولتاژ خروجی به ازای تغییر ۱ اهم در مقاومت، ۲ میلی‌ولت تغییر کند، این مقدار یک حساسیت مطلق است.

2.3.2 حساسیت نسبی (Relative or Normalized Sensitivity)

در بسیاری از موارد، بهتر است حساسیت را به صورت نسبی (بدون بعد) بیان کنیم تا بتوان پارامترهای مختلف را مقایسه کرد.
در این صورت:

\[S_{p}^{y} = \frac{p}{y} \cdot \frac{\partial y}{\partial p}\]

تفسیر: اگر $ S_{p}^{y} = 0.5 $ باشد، یعنی تغییر ۱٪ در پارامتر $ p $، باعث تغییر ۰٫۵٪ در خروجی $ y $ می‌شود.
این نوع حساسیت برای مقایسه بین مدارهای مختلف یا پارامترهای متفاوت بسیار مفید است.

2.4 روش‌های محاسبه حساسیت

سه رویکرد کلی برای محاسبه حساسیت در مدارهای دیودی وجود دارد:

2.4.1 روش تحلیلی (Analytical Method)

در این روش، با استفاده از مدل ریاضی مدار (مانند معادله شاکلی برای دیود) مشتق خروجی نسبت به پارامتر مورد نظر محاسبه می‌شود.

مثلاً برای جریان دیود:

\[I_D = I_S \left( e^{\frac{V_D}{nV_T}} - 1 \right)\]

حساسیت جریان دیود نسبت به ولتاژ دو سر دیود برابر است با:

\[S_{V_D}^{I_D} = \frac{\partial I_D}{\partial V_D} = \frac{I_S}{nV_T} e^{\frac{V_D}{nV_T}}\]

این روش دقیق است، اما نیاز به روابط تحلیلی مدار دارد.
برای مدارهای ساده مثل دیود، به‌خوبی قابل استفاده است.

2.4.2 روش عددی (Numerical Method)

در این روش، خروجی مدار برای چند مقدار متفاوت از پارامتر محاسبه می‌شود و سپس مشتق تقریب زده می‌شود:

\[S_{p}^{y} \approx \frac{y(p + \Delta p) - y(p)}{\Delta p}\]

این روش ساده است و در شبیه‌سازی‌های کامپیوتری (مثلاً با PySpice) بسیار کاربرد دارد.
خطای آن به انتخاب مقدار $ \Delta p $ بستگی دارد (هرچه کوچکتر، دقیق‌تر).

2.4.3 روش شبیه‌سازی (Simulation-Based)

در این حالت، از نرم‌افزارهایی مثل LTspice، Multisim یا PySpice استفاده می‌شود.
در شبیه‌سازی می‌توان:

• پارامترها (مثل مقاومت، دما، $ I_S $) را به‌صورت پارامتری تغییر داد،
• خروجی (مثل $ I_D $ یا $ V_{out} $) را برای هر تغییر رسم کرد،
• از نمودارها برای استخراج حساسیت استفاده نمود.

مزیت: نتایج واقعی‌تر، با در نظر گرفتن مدل غیرخطی قطعات.
عیب: نیازمند شبیه‌سازی دقیق و تنظیم گام مناسب تغییر پارامتر است.

2.5 اهمیت تحلیل حساسیت در طراحی مدارهای عملی

در مدارهای واقعی، قطعات ایده‌آل نیستند و عواملی مانند موارد زیر بر عملکرد تأثیر دارند:

عامل تغییر	توضیح	مثال اثر در مدار دیودی
تلرانس قطعات	تفاوت بین مقدار اسمی و واقعی مقاومت یا خازن	تغییر نقطه کار دیود
دمای محیط	تغییر در $ V_T $ و $ I_S $	تغییر جریان دیود و ولتاژ شکست
تغییر منبع تغذیه	نوسان در ولتاژ منبع	تغییر در جریان بایاس یا ولتاژ خروجی
تغییر مدل قطعه	مثلاً نوع دیود یا ماده سازنده	تغییر در پارامترهای مدل شاکلی

بنابراین تحلیل حساسیت کمک می‌کند تا:

• پارامترهای بحرانی شناسایی شوند،
• مدارهایی با پایداری بالا طراحی گردند،
• اثرات دما و تلرانس با جبران‌سازی کاهش یابند.

2.6 جمع‌بندی بخش تئوری

تحلیل حساسیت ابزاری برای پیش‌بینی پایداری مدار در برابر تغییرات جزئی است.
در مدارهای دیودی، حساسیت می‌تواند نسبت به:

• ولتاژ منبع،
• مقاومت‌های مدار،
• دما،
• یا جریان اشباع دیود بررسی شود.

استفاده از ترکیب روش‌های تحلیلی و شبیه‌سازی، دید کاملی از رفتار مدار می‌دهد.
در بخش‌های بعدی، این مفاهیم در مدارهای عملی (مدار دیودی ساده و مدار یکسوساز) به‌صورت کمی تحلیل خواهند شد.

3.تحلیل حساسیت در مدارهای دیودی ساده

در این بخش، هدف ما بررسی نحوه‌ی تغییر جریان و ولتاژ دیود در برابر تغییرات پارامترهای مختلف مانند:

• ولتاژ منبع $ V_S $
• مقاومت سری $ R $
• دمای محیط $ T $
• جریان اشباع دیود $I_S$

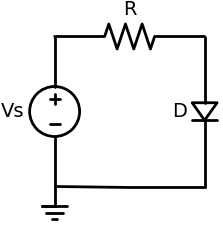
است. مدار مورد مطالعه شامل یک منبع ولتاژ DC، یک مقاومت سری و یک دیود سیلیکونی است.

import schemdraw
import schemdraw.elements as elm

with schemdraw.Drawing() as d:
    d.config(unit=3)
    V1 = d.add(elm.SourceV(label='Vs'))
    d.add(elm.Resistor(label='R').right())
    d.add(elm.Diode(label='D').down())
    d.add(elm.Line().left())
    d.add(elm.Ground())
    d.draw()

مدار ساده دیودی

3.1 مفروضات و پارامترهای پایه

در تمام تحلیل‌ها از معادلهٔ شوکلی برای دیود استفاده می‌کنیم: \(I_D = I_S\left(e^{\dfrac{V_D}{nV_T}} - 1\right)\) با پارامترهای مرجع (مثال عددی):

• $V_S = 5\text{V}$
• $R = 1\text{k}\Omega$
• $n = 1$
• $T = 300\text{K}$ → $V_T = \dfrac{kT}{q} \approx 25.85\text{mV}$
• $I_S = 1\times10^{-12}\text{A}$ (مثال)
• تقریبی برای نقطه‌کار: $V_D \approx 0.7\text{V}$ ⇒ $I_D \approx$ $V_S$ - $V_D/R = (5-0.7)/1000 = 4.3\text{mA}$

توضیح: مقدار $V_D$ دقیق با حل غیرخطی معادلهٔ KVL + شوکلی به دست می‌آید؛ برای تقریب سریع از (0.65!-!0.75)V استفاده می‌کنیم.

3.2 معادلات پایه (KVL ، شوکلی)

KVL: \(V_S = I_D R + V_D\)

دیود (Shockley): \(I_D = I_S\left(e^{\frac{V_D}{nV_T}} - 1\right)\)

برای حل نقطه‌کار، معادلهٔ ترکیبی زیر را باید حل عددی کرد: \(V_S = R,I_S\left(e^{\frac{V_D}{nV_T}} - 1\right) + V_D\)

3.3 حساسیت جریان دیود نسبت به ولتاژ منبع $S_{V_S}^{I_D}$

برای یافتن حساسیت جریان دیود نسبت به ولتاژ منبع داریم:

\[S_{V_S}^{I_D} = \frac{V_S}{I_D} \cdot \frac{\partial I_D}{\partial V_S}\]

از معادله‌ی مدار:

\[V_S = I_D R + V_D\]

با مشتق‌گیری نسبت به $( V_S $):

\[1 = R \frac{dI_D}{dV_S} + \frac{dV_D}{dV_S}\]

اما از معادله‌ی شوکلی:

\[\frac{dI_D}{dV_D} = \frac{I_D}{n V_T}\]

با استفاده از قاعده زنجیره‌ای:

\[\frac{dI_D}{dV_S} = \frac{dI_D}{dV_D} \cdot \frac{dV_D}{dV_S}\]

و با ترکیب دو رابطه بالا، نتیجه می‌شود:

\[\frac{dI_D}{dV_S} = \frac{1}{R + \frac{nV_T}{I_D}}\]

پس:

\(S_{V_S}^{I_D} = \frac{V_S}{I_D} \cdot \frac{1}{R + \frac{nV_T}{I_D}}\) بنابراین حساسیت نسبی: \(\boxed{S_{V_S}^{I_D} = \frac{V_S}{I_D}\cdot\frac{1}{R + \dfrac{nV_T}{I_D}}}\)

تفسیر:

• اگر $R$ بزرگ شود، مخرج بزرگ می‌شود ⇒ $\dfrac{dI_D}{dV_S}$ کوچک می‌شود ⇒ حساسیت کمتر.
• وقتی $I_D$ بزرگ است، $nV_T/I_D$ کوچک می‌شود و مدار نسبت به $V_S$ پایدارتر است.

مثال عددی (با مقادیر پایه): \(V_S=5\text{V} , \ I_D=4.3\times10^{-3}\text{A} , \ R=1000\Omega , \ nV_T=0.02585\text{V}\) محاسبهٔ میانی: \(\frac{nV_T}{I_D} = \frac{0.02585}{0.0043} \approx 6.01\ \Omega\) \(R + \frac{nV_T}{I_D} \approx 1006.01\ \Omega\) \(\frac{dI_D}{dV_S} \approx \frac{1}{1006.01} \approx 9.94\times10^{-4}\ \text{A/V}\) \(S_{V_S}^{I_D} \approx \frac{5}{0.0043}\times 9.94\times10^{-4} \approx 1.156\)

یعنی: افزایش ۱٪ در $V_S$ حدود $1.156%$ افزایش در $I_D$ ایجاد می‌کند.

3.3.0 تحلیل نموداری حساسیت جریان دیود نسبت به ولتاژمنبع

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

I_S = 1e-12
n = 1
k = 1.38e-23
q = 1.6e-19
T = 300
V_T = (k*T)/q
R = 1e3

def diode_current(V_D):
    return I_S*(np.exp(V_D/(n*V_T)) - 1)

def diode_eq(V_D, V_S):
    return V_S - R*diode_current(V_D) - V_D

Vs_range = np.linspace(0, 5, 100)
Id_vs = []
for Vs in Vs_range:
    Vd = fsolve(diode_eq, 0.7, args=(Vs))[0]
    Id_vs.append(diode_current(Vd))

plt.plot(Vs_range, Id_vs)
plt.title("Id vs Vs")
plt.xlabel("Vs (V)")
plt.ylabel("Id (A)")
plt.grid(True)
plt.show()

تحلیل نموداری حساسیت جریان دیود نسبت به ولتاژمنبع

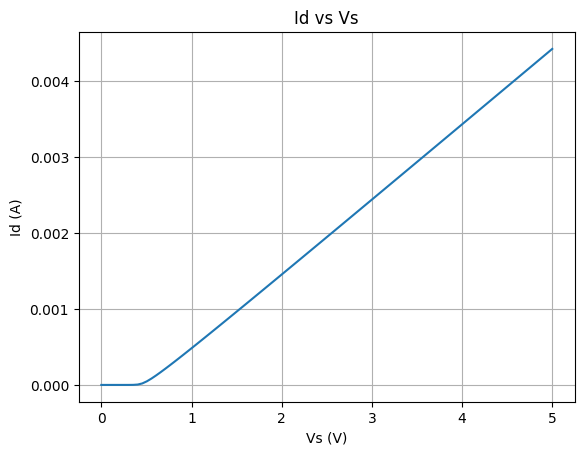
3.4 حساسیت ولتاژ دیود نسبت به مقاومت سری $S_R^{V_D}$

از KVL: \(V_D = V_S - I_D R\) مشتق نسبت به (R): \(\frac{dV_D}{dR} = -I_D - R\frac{dI_D}{dR} \qquad(3)\)

از شوکلی و قاعدهٔ زنجیره (شبیه مراحل قبل) می‌توان نشان داد: \(\frac{dI_D}{dR} = \frac{-I_D^2}{nV_T + R I_D}\)

جایگذاری در (3): \(\frac{dV_D}{dR} = -I_D + \frac{R I_D^2}{nV_T + R I_D}\)

حساسیت نسبی: \(\boxed{S_R^{V_D} = \frac{R}{V_D}\cdot(-I_D + \frac{R I_D^2}{nV_T + R I_D})}\)

مثال عددی (با مقادیر پایه): محاسبات میانی: \(R I_D^2 = 1000 \times (0.0043)^2 \approx 0.01849\) \(nV_T + R I_D = 0.02585 + 4.3 \approx 4.32585\) \(\frac{R I_D^2}{nV_T + R I_D} \approx \frac{0.01849}{4.32585} \approx 0.004276,\text{V/}\Omega\) \(\frac{dV_D}{dR} \approx -0.0043 + 0.004276 \approx -2.4\times10^{-5}\ \text{V/}\Omega\) \(S_R^{V_D} \approx \frac{1000}{0.7}\times(-2.4\times10^{-5}) \approx -0.0343\)

یعنی: افزایش ۱٪ در $R$ باعث ≈ $-0.034%$ تغییر در $V_D$ می‌شود — حساسیت بسیار کوچک (ولتاژ دیود تقریباً تحت‌تأثیر R نیست در این نقطه‌کار).

تفسیر:

• مقاومت سری تأثیر بزرگ‌تری بر جریان (مطلق) دارد، اما اثر آن روی ولتاژ دیود $V_D$ (نسبی) کوچک است چون ولتاژ دیود نزدیک مقدار ثابت (نیمه‌رسانا) است.

3.4.0 تحلیل نموداری حساسیت ولتاژ دیود نسبت به مقاومت سری

R_values = [500, 1000, 2000, 5000]
Vd_R = []
for R_ in R_values:
    def diode_eq(V_D):
        return 5 - R_*I_S*(np.exp(V_D/(n*V_T)) - 1) - V_D
    Vd = fsolve(diode_eq, 0.7)[0]
    Vd_R.append(Vd)

plt.plot(R_values, Vd_R, marker='o')
plt.title("Vd vs R")
plt.xlabel("R (Ohm)")
plt.ylabel("Vd (V)")
plt.grid(True)
plt.show()

تحلیل نموداری حساسیت ولتاژ دیود نسبت به مقاومت سری

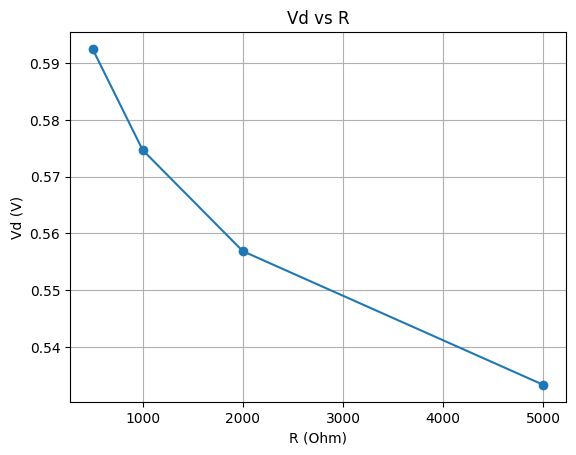
3.5 حساسیت نسبت به دما $S_T^{V_D}$

شروع از معادله شوکلی \(I_D = I_S \left(e^{\frac{V_D}{nV_T}} - 1\right)\)

که در آن:

• $ I_D $: جریان دیود
• $ I_S $: جریان اشباع معکوس (وابسته به دما)
• $ V_D $: ولتاژ دو سر دیود
• $ V_T = \frac{kT}{q} $: ولتاژ حرارتی
• $ n $: ضریب ایده‌آل (بین ۱ تا ۲)
• $ k $: ثابت بولتزمن

• $ q $: بار الکترون

• $V_T = \dfrac{kT}{q}$ وابسته به دماست.
• همچنین $I_S$ به صورت نمایی با دما تغییر می‌کند: \(I_S(T) = I_{S0}\left(\frac{T}{T_0}\right)^3 \exp!\left(-\dfrac{E_g}{k}!\left(\frac{1}{T}-\frac{1}{T_0}\right)\right)\)

با افزایش دما معمولاً $I_S$ افزایش و $V_D$ کاهش می‌یابد.

تقریب مهندسی (خطی‌سازی عملی):

در عمل برای دیود سیلیکونی، میزان تغییر $V_D$ با دما در حدود $-1.5$ تا$-3$ $\text{mV}/^\circ\text{C}$ است. یک مقدار میانگینِ پذیرفته‌شده ≈ $-2 \text{mV}/^\circ\text{C}$.

\[\frac{dV_D}{dT} \approx -2 \text{ mV/°C} = -0.002 \text{ V/K}\]

این عدد از اندازه‌گیری‌های تجربی برای دیودهای سیلیکونی معمولی مثل 1N4148 یا 1N4001 گرفته می‌شود.

مثال عددی (با تقریب خطی):

در تحلیل حساسیت، معمولاً از تعریف زیر استفاده می‌کنیم:

\[S_T^{V_D} = \frac{T}{V_D} \cdot \frac{dV_D}{dT}\]

که بیان می‌کند چند درصد تغییر در $ V_D $ به ازای درصد تغییر در $ T $ اتفاق می‌افتد.

قرار دادن مقدارهای عددی

با فرض‌های معمول برای دیود سیلیکونی:

• $ V_D = 0.7 \text{ V} $
• $ T = 300 \text{ K} $
• $ \frac{dV_D}{dT} = -0.002 \text{ V/K} $

داریم:

\[S_T^{V_D} = \frac{300}{0.7} \times (-0.002) = -0.857\]

یعنی اگر دما ۱٪ زیاد شود (حدود ۳K)، ولتاژ دیود حدود ۰.857٪ کاهش پیدا می‌کند. بنابراین حساسیت قابل توجه است (تقریباً خطی در بازه‌ی محدود دما).

دلیل استفاده از تقریب خطی: در بازه‌ی ۲۰–۸۰ درجه سانتی‌گراد، رفتار $ V_D $ نسبت به $ T $ تقریباً خطی است.

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

# ثابت‌ها
k = 1.38e-23
q = 1.6e-19
n = 1
R = 1000
V_S = 5

# مقادیر مرجع در 300K
I_S0 = 1e-12
T0 = 300
E_g = 1.12 * q  # انرژی باند گپ سیلیکون

T_values = np.linspace(250, 400, 100)
Vd_T = []

for T_ in T_values:
    V_T_ = (k * T_) / q
    # جریان اشباع وابسته به دما:
    I_S_T = I_S0 * (T_/T0)**3 * np.exp(-E_g/k * (1/T_ - 1/T0))

    def eq(V_D):
        return V_S - R*I_S_T*(np.exp(V_D/(n*V_T_)) - 1) - V_D

    Vd = fsolve(eq, 0.7)[0]
    Vd_T.append(Vd)

plt.plot(T_values, Vd_T, color='red')
plt.title("Diode Voltage vs Temperature (Realistic)")
plt.xlabel("Temperature (K)")
plt.ylabel("Diode Voltage Vd (V)")
plt.grid(True)
plt.show()

تحلیل حساسیت ولتاژ دیود نسبت به دما

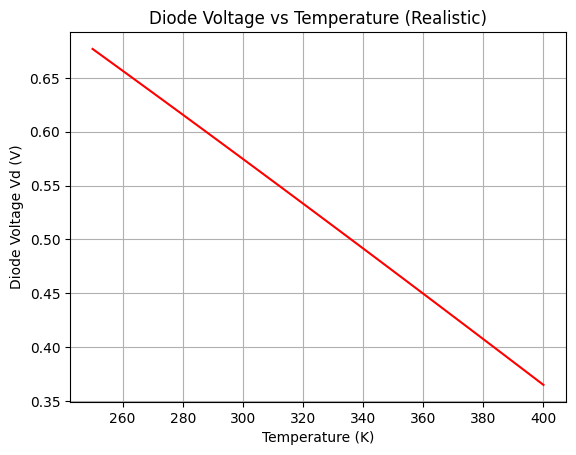
3.6 حساسیت جریان دیود نسبت به $I_S$ (جریان اشباع)

چون در محدودهٔ نمایی $I_D \approx I_S e^{V_D/(nV_T)}$، به‌صورت مستقیم $I_D$ با $I_S$ نسبت مستقیم دارد اگر $V_D$ ثابت بماند. اما در مدار ما $V_D$ هم تابع $I_S$ است (KVL برقرار است) بنابراین اثر واقعی کمتر از ۱:۱ خواهد بود.

3.6.1 مدل و مفروضات

در ناحیهٔ نمایی فرض می‌کنیم (برای سادگی و آشنایی با نتیجهٔ غالب): \(I_D \approx I_S , e^{\dfrac{V_D}{nV_T}}\) و معادلهٔ KVL مدار سری: \(V_S = I_D R + V_D\) (فرضِ $I_D \gg I_S$ برای حذف «-1» در شوکلی)

3.6.2 مشتق‌گیری تحلیلی (در حضور مقاومت سری $R$)

ابتدا مشتق $I_D$ نسبت به $I_S$ را بنابر مدل نمایی بنویسیم، ولی توجه کنیم که $V_D$ تابعِ $I_S$ هم هست (بخاطر KVL):

مستقیماً از مدل نمایی: \(\frac{\partial I_D}{\partial I_S}\Big|_{V_D} = e^{\frac{V_D}{nV_T}} = \frac{I_D}{I_S}\) این اگر $V_D$ ثابت بماند یعنی اگر ولتاژ دیود قفل باشد؛ اما در مدار ما $V_D$ تغییر می‌کند. پس با زنجیره‌ای باید رفتار کامل را محاسبه کنیم.

مشتق کلی (با در نظر گرفتن تغییر $V_D$) را بنویسیم: \(\frac{dI_D}{dI_S} = \frac{I_D}{I_S} + \frac{I_D}{nV_T}\cdot\frac{dV_D}{dI_S}. \tag{A}\)

از KVL داریم: \(0 = R\frac{dI_D}{dI_S} + \frac{dV_D}{dI_S} \quad\Rightarrow\quad \frac{dV_D}{dI_S} = -R\frac{dI_D}{dI_S}. \tag{B}\)

جایگذاری (B) در (A): \(\frac{dI_D}{dI_S} = \frac{I_D}{I_S} - \frac{I_D}{nV_T}R\frac{dI_D}{dI_S}.\)

حالا جمع‌آوری جملاتِ $\dfrac{dI_D}{dI_S}$ در یک طرف: \(\left(1 + \frac{I_D R}{nV_T}\right)\frac{dI_D}{dI_S} = \frac{I_D}{I_S}.\)

بنابراین: \(\boxed{\displaystyle \frac{dI_D}{dI_S} = \frac{\dfrac{I_D}{I_S}}{1 + \dfrac{I_D R}{nV_T}} } \tag{1}\)

حالا حساسیت نسبیِ بدون‌بعد (normalized sensitivity) تعریف می‌شود: \(S_{I_S}^{I_D} = \frac{I_S}{I_D}\cdot\frac{dI_D}{dI_S}.\) با جایگذاری (1) داریم:

\[\boxed{\displaystyle S_{I_S}^{I_D} = \frac{1}{1 + \dfrac{I_D R}{nV_T}} } \tag{2}\]

3.6.3 تفسیر فرمول $S_{I_S}^{I_D}$

• اگر $R \to 0$ (منبع ولتاژ با امپدانس داخلی نزدیک صفر، یا مدار بدون محدودکننده)، آنگاه $\dfrac{I_D R}{nV_T}\to 0$ و $S_{I_S}^{I_D}\to 1$. یعنی در این حد جریان خروجی نسبت مستقیم و 1:1 به $I_S$ وابسته است — (اگر $I_S$ ۱۰٪ تغییر کند، $I_D$ هم تقریباً ۱۰٪ تغییر می‌کند) — چون ولتاژ دیود ثابت فرض می‌شود و منبع تغذیه ولتاژ را تحمیل می‌کند.
• اگر $I_D R \gg nV_T$ (مثلاً مقاومت سری بزرگ یا جریان بزرگ) آنگاه $S_{I_S}^{I_D}\ll 1$. یعنی تأثیر تغییر $I_S$ روی $I_D$ بسیار کم می‌شود، چون مقاومت سری جریان را «محدود» می‌کند و دیود نمی‌تواند آزادانه تغییر کند.
• بیان فیزیکی: مقاومت سری باعث می‌شود تغییرات در مشخصهٔ داخلی دیود (مثل $I_S$) بیشتر در ولتاژ دیود جبران شوند تا در جریان؛ بنابراین اثر $I_S$ تضعیف می‌شود.

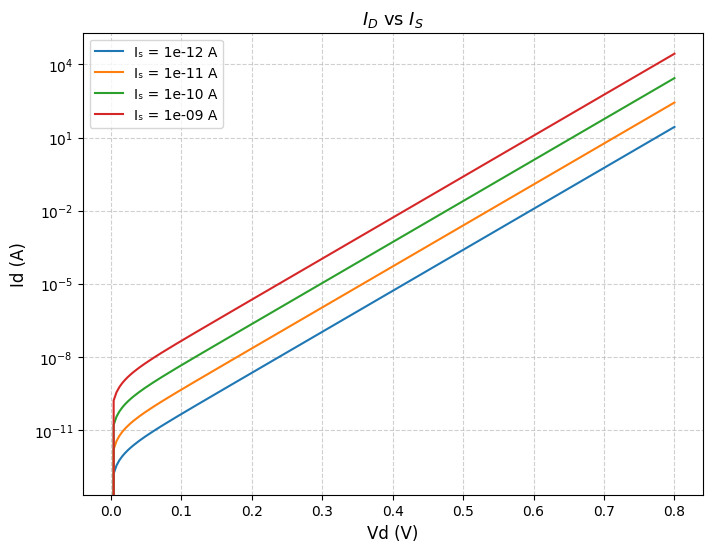
3.6.4تحلیل نموداری حساسیت جریان دیود نسبت به $I_S$ (جریان اشباع)

Vd = np.linspace(0, 0.8, 200)

# مقادیر مختلف جریان اشباع
Is_values = [1e-12, 1e-11, 1e-10, 1e-9]

# محاسبه جریان دیود برای هر مقدار Is
plt.figure(figsize=(8,6))
for Is in Is_values:
    Id = Is * (np.exp(Vd / (n * Vt)) - 1)
    plt.plot(Vd, Id, label=f"Iₛ = {Is:.0e} A")

plt.title("$I_D$ vs $I_S$", fontsize=13)
plt.xlabel("Vd (V)", fontsize=12)
plt.ylabel("Id (A)", fontsize=12)
plt.yscale("log")  # برای نمایش بهتر در مقیاس لگاریتمی
plt.grid(True, which="both", linestyle="--", alpha=0.6)
plt.legend()
plt.show()

تحلیل نموداری حساسیت جریان دیود نسبت به جریان اشباع

3.7 حساسیت ولتاژ دیود نسبت به $I_S$

می‌خواهیم $dV_D/dI_S$ و حساسیت نسبی $S_{I_S}^{V_D} = \dfrac{I_S}{V_D}\dfrac{dV_D}{dI_S}$ را هم پیدا کنیم.

با استفاده از (B) و (1): \(\frac{dV_D}{dI_S} = -R\frac{dI_D}{dI_S} = -R \cdot \frac{\dfrac{I_D}{I_S}}{1 + \dfrac{I_D R}{nV_T}}.\)

پس: \(\boxed{\displaystyle \frac{dV_D}{dI_S} = -\frac{R I_D / I_S}{1 + \dfrac{I_D R}{nV_T}} } \tag{3}\)

و حساسیت نسبی: \(\boxed{\displaystyle S_{I_S}^{V_D} = \frac{I_S}{V_D}\cdot\frac{dV_D}{dI_S} = -\frac{R I_D}{V_D\left(1 + \dfrac{I_D R}{nV_T}\right)} } \tag{4}\)

تفسیر: علامت منفی نشان می‌دهد که افزایش $I_S$ منجر به کاهش $V_D$ می‌شود (چون برای برقراری KVL و تنظیم جریان، ولتاژ دیود کمی پایین می‌آید).

3.7.1 مثال عددی

پارامترها (مثال):

• $V_S=5\ \text{V}$
• $R=1{,}000\ \Omega$
• $V_D\approx 0.7\ \text{V}$
• $I_D\approx (V_S - V_D)/R = (5-0.7)/1000 = 0.0043\ \text{A}$
• $nV_T \approx 0.02585\ \text{V}) (T ≈ 300 K$

محاسبهٔ عددی: \(\frac{I_D R}{nV_T} = \frac{0.0043\times 1000}{0.02585} \approx 166.4\)

پس از (2): \(S_{I_S}^{I_D} \approx \frac{1}{1 + 166.4} \approx 0.00598 \approx 0.006%.\) یعنی: اگر $I_S$ ۱٪ تغییر کند، $I_D$ فقط حدود (0.006%) تغییر می‌کند — اثر بسیار کوچک.

برای ولتاژ دیود از (4): \(S_{I_S}^{V_D} \approx -\frac{R I_D}{V_D(1 + 166.4)} = -\frac{4.3}{0.7\times 167.4} \approx -0.0367.\) یعنی: اگر $I_S$ ۱٪ افزایش یابد، $V_D$ حدود (0.037%) کاهش می‌یابد (نسبتاً کم ولی قابل توجه در بعضی طراحی‌ها).

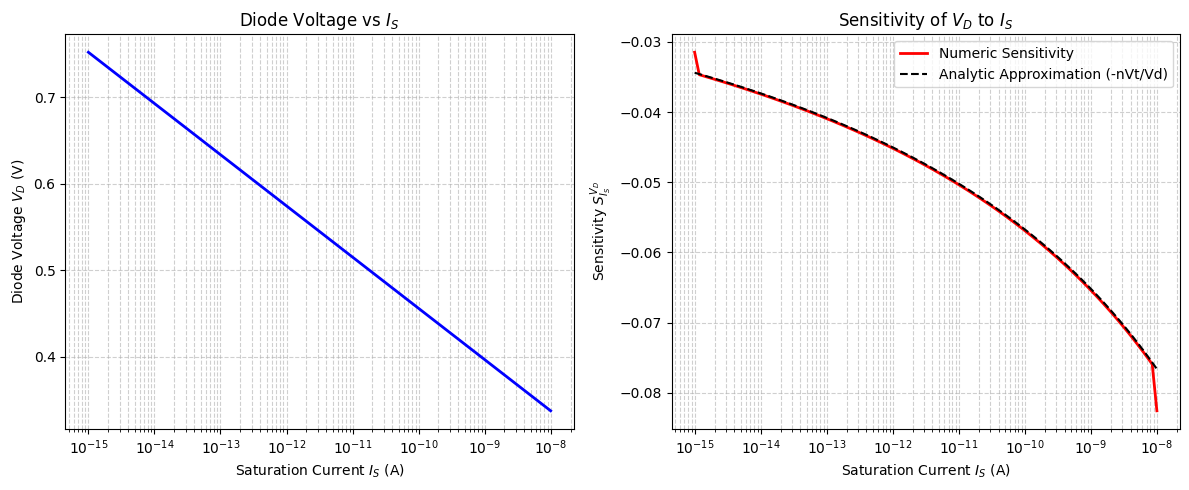
3.7.2 تحلیل نموداری حساسیت ولتاژ دیود نسبت به $I_S$ (جریان اشباع)

V_S = 5       
R = 1000       
n = 1 
T = 300
k = 1.38064852e-23  
q = 1.60217662e-19  
V_T = (k * T) / q   

I_S_values = np.logspace(-15, -8, 100)
V_D_values = []

for I_S in I_S_values:
    func = lambda V_D: V_S - R * (I_S * np.exp(V_D / (n * V_T))) - V_D
    V_D_solution = fsolve(func, 0.7)[0]
    V_D_values.append(V_D_solution)

V_D_values = np.array(V_D_values)

dVd_dIs = np.gradient(V_D_values, I_S_values)
S_num = (I_S_values / V_D_values) * dVd_dIs

# تقریب تحلیلی: S ≈ -nVt/Vd
S_approx = -n * V_T / V_D_values

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.semilogx(I_S_values, V_D_values, color='blue', linewidth=2)
plt.xlabel("Saturation Current $I_S$ (A)")
plt.ylabel("Diode Voltage $V_D$ (V)")
plt.title("Diode Voltage vs $I_S$")
plt.grid(True, which="both", linestyle='--', alpha=0.6)

plt.subplot(1, 2, 2)
plt.semilogx(I_S_values, S_num, label='Numeric Sensitivity', color='red', linewidth=2)
plt.semilogx(I_S_values, S_approx, '--', label='Analytic Approximation (-nVt/Vd)', color='black')
plt.xlabel("Saturation Current $I_S$ (A)")
plt.ylabel("Sensitivity $S_{I_S}^{V_D}$")
plt.title("Sensitivity of $V_D$ to $I_S$")
plt.legend()
plt.grid(True, which="both", linestyle='--', alpha=0.6)

plt.tight_layout()
plt.show()

تحلیل نموداری حساسیت ولتاژ دیود نسبت به جریان اشباع

3.8 خلاصهٔ نتایج و تفسیر (نتیجه‌گیری بخش)

• حساسیت نسبت به (V_S): معمولاً نزدیک به 1 (در مقیاس درصدی) یا کمی بیشتر/کمتر بسته به مقدار R و نقطه‌کار. در مثال عددی ما $S_{V_S}^{I_D}\approx 1.156$ — یعنی ۱٪ تغییر در $V_S$ ≈ ۱.۱۵۶٪ تغییر در $I_D$. → بنابراین منابع تغذیه ناپایدار می‌توانند جریان را به‌طور معناداری تغییر دهند.

• حساسیت نسبت به (R): اثر تغییر R روی ولتاژ دیود $V_D$ معمولاً کوچک است (مثال: $S_R^{V_D}\approx -0.034$). اما اثر R روی مقدار مطلق جریان چشمگیر است (چون $I\propto1/R$ در ناحیه‌ای که $V_D$ تقریباً ثابت است). → برای کنترل جریان و کاهش حساسیت به $V_S$ از مقاومت سری استفاده می‌شود.

• حساسیت نسبت به دما: ولتاژ دیود به‌طور محسوس با دما تغییر می‌کند (چند میلی‌ولت بر هر درجه). در مثال ما، حساسیت نسبی به دما بزرگ و منفی است (نمونه: $S_T^{V_D}\approx -0.857$ با تقریب خطی). → مهم در طراحی‌هایی که دمای کاری متغیر است: نیاز به جبران‌سازی حرارتی یا اجتناب از استفاده از $V_D$ به‌عنوان مرجع دقیق.

• فرمول کلیدی برای حساسیت جریان نسبت به $I_S$ در مدار سری (دیود + مقاومت) این است: \(S_{I_S}^{I_D} = \frac{1}{1 + \dfrac{I_D R}{nV_T}}.\)
• وقتی $I_D R \gg nV_T$، حساسیت بسیار کوچک می‌شود (مقاومت سری اثر $I_S$ را تضعیف می‌کند).
• اگر منبع قوی و $R$ نزدیک صفر باشد، حساسیت تقریباً ۱ است (یعنی $I_D$ تقریباً مستقیم با $I_S$ نسبت دارد).

پارامتر	خروجی	اثر	توضیح
$V_S$	$I_D$	مثبت	افزایش $V_S$ باعث افزایش جریان دیود می‌شود
$R$	$V_D$	منفی	افزایش مقاومت باعث کاهش جریان و ولتاژ دیود می‌شود
$T$	$V_D$	منفی	دما باعث کاهش ولتاژ باند و $V_D$ می‌شود
$I_S$	$V_D$	منفی	افزایش $I_S$ باعث هدایت بهتر و افت ولتاژ کمتر می‌شود

3.9 جدول مقایسهٔ حساسیت‌ها (نمونه عددی — مقادیر تقریبی)

توضیح: مقادیر زیر بر اساس مثال عددی ( $V_S=5$V, $R=1\ \text{k}\Omega$, $V_D\approx0.7$V, $I_D\approx4.3$mA, $T=300$K ) محاسبه شده‌اند.

خروجی (y)	پارامتر (x)	$ \dfrac{dy}{dx} $ (تقریبی)	$S_x^y = \dfrac{x}{y}\dfrac{dy}{dx}$ (تقریبی)	تفسیر
$I_D$	$V_S$	$9.94\times10^{-4}\ \text{A/V}$	$\approx 1.156$	۱٪ ↑ در $V_S$ → ≈۱.۱۵۶٪ ↑ در $I_D$
$V_D$	$R$	$-2.4\times10^{-5}\ \text{V/}\Omega$	$\approx -0.034$	تأثیر بسیار کوچک (نسبی) بر $V_D$
$V_D$	$T$	$\approx -0.002\ \text{V/K}$ (خطی)	$\approx -0.857$	تغییر دما قویاً $V_D$ را کاهش می‌دهد
$I_D$	$V_D$	$\dfrac{I_D}{nV_T}\approx 166.3\ \text{A/V}$	$\dfrac{V_D}{nV_T}\approx 27.07$ (نسبی)	جریان بسیار حساس به تغییر $V_D$ (ولتاژ نزدیکی 0.7V)

نکته: سطر آخر (حساسیت $I_D$ نسبت به $V_D$) نشان دهندهٔ شیب تند مشخصهٔ دیود است: تغییر اندک در ولتاژ دیود (میلی‌ولت) می‌تواند جریان را به مقدار زیادی تغییر دهد.

4. تحلیل حساسیت در کاربردهای خاص دیود

1. یکسوساز نیم‌موج (Half-wave rectifier) — حساسیت ولتاژ خروجی نسبت به تغییرات ولتاژ ورودی و بار

4.1 مدار یکسوساز نیم‌موج (Half-wave rectifier)

4.1.1 شرح مدار و فرض‌ها

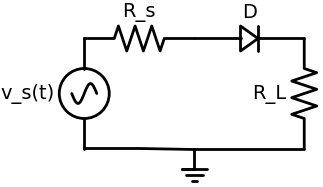
مدار پایه مورد نظر: منبع AC سینوسی $v_s(t)$ با امپدانس داخلی یا مقاومت سری $R_s$، دیود $D$ و بار مقاومتی $R_L$.

فرض‌ها:

• بررسی در حالت پیوسته‌ی هدایت (قله‌های ولتاژ که دیود هدایت می‌کند).
• در ناحیه هدایت، جریان بار $I_D = \dfrac{V_D}{R_L}$ (ولتاژ روی دیود برابر ولتاژ روی بار).
• از ولتاژ‌فوروارد دیود می‌توان یا معادله شوکلی استفاده کرد یا برای سادگی $V_D$ را ولتاژ روی بار در نظر گرفت.

4.1.2 شماتیک مدار یکسوساز نیم‌موج

کد زیر مدار را با کتابخانه‌ی Schemdraw رسم می‌کند.

import schemdraw
import schemdraw.elements as elm
with schemdraw.Drawing() as d:
    d.config(unit=2.2)
    d += elm.SourceSin().up().label('v_s(t)')
    d += elm.Resistor().right().label('R_s')
    d += elm.Diode().right().label('D')
    d += elm.Resistor().down().label('R_L')
    d += elm.Line().left()
    d += elm.Ground()
    d += elm.Line().left()
    d.draw()

شماتیک مدار یکسوساز نیم‌موج

4.1.3 KVL در لحظه‌ی هدایت (peak conduction)

در لحظه‌ای که دیود هدایت می‌کند، حلقه‌ی معادل داریم:

\[v_s(t) = I_D R_s + V_D\]

و چون $I_D = \dfrac{V_D}{R_L}$ داریم:

\[v_s(t) = \frac{V_D}{R_L} R_s + V_D = V_D\left(1 + \frac{R_s}{R_L}\right)\]

بنابراین ولتاژ لحظه‌ای روی بار:

\[V_D = \frac{v_s(t)}{1 + \dfrac{R_s}{R_L}} \tag{1}\]

حساسیت ولتاژ خروجی نسبت به ولتاژ ورودی (در حالت هدایت):

مشتق مطلق:

\[\frac{\partial V_D}{\partial v_s} = \frac{1}{1 + \dfrac{R_s}{R_L}}\]

حساسیت نسبی (normalized):

\[S_{v_s}^{V_D} = \frac{v_s}{V_D}\cdot\frac{\partial V_D}{\partial v_s}\]

اما از (1) داریم $v_s/V_D = 1 + \dfrac{R_s}{R_L}$ پس:

\[S_{v_s}^{V_D} = 1\]

تفسیر: حساسیت نسبی $S_{v_s}^{V_D}=1$ یعنی درصد تغییر $V_D$ برابر درصد تغییر $v_s$ است،
اما به دلیل تقسیم ولتاژ، دامنه‌ی مطلق خروجی کمتر از ورودی است. هرچه $R_L$ بزرگ‌تر باشد، این اثر کمتر می‌شود.

حساسیت نسبت به تغییر بار $R_L$:

از (1) می‌توان $V_D$ را به‌صورت تابع $R_L$ نوشت:

\[V_D = \frac{v_s}{1 + R_s/R_L} = v_s \cdot \frac{R_L}{R_L + R_s}\]

مشتق نسبت به $R_L$:

\[\frac{\partial V_D}{\partial R_L} = v_s \cdot \frac{R_s}{(R_L + R_s)^2}\]

پس حساسیت نسبی:

\[S_{R_L}^{V_D} = \frac{R_L}{V_D}\cdot\frac{\partial V_D}{\partial R_L} = \frac{R_L}{v_s\frac{R_L}{R_L+R_s}}\cdot v_s \frac{R_s}{(R_L+R_s)^2} = \frac{R_s}{R_L+R_s}\]

تفسیر:
اگر $R_s \ll R_L$ (منبع قوی / بار سنگین) حساسیت کم است؛
اما اگر $R_s$ قابل‌مقایسه با $R_L$ باشد، تغییرات بار تأثیر زیادی روی خروجی دارد.

4.1.4 نتیجه‌گیری (یکسوساز)

• حساسیت نسبی $S_{v_s}^{V_D}=1$ ولی ضریب مطلق $\partial V_D/\partial v_s$ توسط تقسیم ولتاژ کاهش می‌یابد.
• برای خروجی پایدارتر، باید $R_s$ کوچک و $R_L$ بزرگ انتخاب شود.
• در طراحی‌های دقیق، استفاده از فیلتر RC یا تنظیم سطح DC خروجی نیز پیشنهاد می‌شود.

5. نتیجه‌گیری و ارائه راهکارهای طراحی

5.1 جمع‌بندی نتایج تحلیل حساسیت

در مراحل قبلی دیدیم که مقدار جریان و ولتاژ در یک مدار دیودی، به پارامترهای مختلفی مثل:

• ولتاژ منبع تغذیه (Vs)
• مقاومت سری (R)
• دمای محیط
• و پارامترهای داخلی دیود مثل جریان اشباع (Is) و ضریب n

حساس هستند.
یعنی اگر هرکدام از این پارامترها کمی تغییر کنند، ممکن است ولتاژ یا جریان دیود به‌طور قابل‌توجهی تغییر کند.

به این می‌گوییم حساسیت بالا — مدار نسبت به تغییرات محیط یا قطعات واکنش زیادی نشان می‌دهد.

5.2 شناسایی پارامترهای با حساسیت بالا

با بررسی نمودارها در بخش قبل، معمولاً متوجه می‌شویم که:

• ولتاژ منبع (Vs) تأثیر زیادی دارد (افزایش Vs → افزایش جریان دیود به‌شدت زیاد می‌شود).
• دمای محیط (T) نیز اثر قابل‌توجهی دارد، چون با افزایش دما، جریان اشباع ( I_S ) زیاد می‌شود و منحنی مشخصه دیود تغییر می‌کند.
• مقاومت سری (R) باعث محدود شدن جریان و کنترل حساسیت مدار می‌شود، پس نقش کلیدی در پایداری دارد.

بنابراین Vs و T معمولاً جزو حساس‌ترین پارامترها هستند.

5.3 راهکارهایی برای کاهش حساسیت مدار

برای اینکه مدار در برابر تغییرات مقاوم‌تر و پایدارتر شود، می‌توانیم از چند روش استفاده کنیم:

5.3.1 استفاده از فیدبک (Feedback)

فیدبک یعنی بخشی از خروجی مدار را دوباره به ورودی برگردانیم تا تغییرات خودبه‌خود جبران شوند.
مثلاً در مدارهای تنظیم ولتاژ (Voltage Regulator)، از دیود زنر یا اپ‌امپ برای ثابت نگه داشتن ولتاژ خروجی استفاده می‌شود.
این باعث می‌شود اگر Vs تغییر کند، ولتاژ دیود تقریباً ثابت بماند.

5.3.2 جبران‌سازی دمایی (Temperature Compensation)

در مدارهایی که دما تغییر زیادی دارد (مثل مدارهای تغذیه یا محیط صنعتی)، باید اثر دما روی دیود جبران شود.
مثلاً:

• استفاده از دیودهای موازی با ضریب حرارتی مخالف، یا
• استفاده از ترمیستور (NTC/PTC) که با تغییر دما مقاومتش تغییر می‌کند و اثر دما را خنثی می‌کند.

5.3.3 انتخاب قطعات با تلرانس پایین

تلرانس یعنی خطای مجاز در مقدار قطعه.
مثلاً یک مقاومت 1kΩ با تلرانس 5٪ ممکن است بین 950 تا 1050Ω باشد.
در طراحی‌های حساس، باید از مقاومت‌ها و دیودهای دقیق‌تر (با تلرانس پایین‌تر مثل 1٪ یا کمتر) استفاده کنیم تا تغییرات ناخواسته کمتر شود.

5.3.4 انتخاب مقدار مناسب مقاومت سری

با زیاد کردن مقدار مقاومت سری R، تغییرات جریان دیود در اثر تغییر Vs یا دما کمتر می‌شود.
چون جریان توسط R کنترل می‌شود، مدار پایدارتر عمل می‌کند (البته اگر R خیلی زیاد شود، ممکن است مدار دیگر به‌درستی کار نکند، پس باید مقدار بهینه انتخاب شود).

نتیجه نهایی

در طراحی مدارهای دیودی، هدف فقط عملکرد صحیح نیست؛
بلکه باید مدار طوری طراحی شود که نسبت به تغییرات محیط و قطعات مقاوم باشد.
برای این کار:

1. پارامترهای حساس را شناسایی کنید.
2. از فیدبک، مقاومت مناسب و قطعات دقیق استفاده کنید.
3. اثر دما را با جبران‌سازی کاهش دهید.

6. مراجع (References)

• Hayt, W. H., Kemmerly, J. E., & Durbin, S. M.
  Engineering Circuit Analysis, 8th Edition, McGraw-Hill, 2012.

• Boylestad, R. L., & Nashelsky, L.
  Electronic Devices and Circuit Theory, 11th Edition, Pearson, 2013.

• Sedra, A. S., & Smith, K. C.
  Microelectronic Circuits, 7th Edition, Oxford University Press, 2014.

• Malvino, A. P., & Bates, D.
  Electronic Principles, 8th Edition, McGraw-Hill, 2012.

• Horowitz, P., & Hill, W.
  The Art of Electronics, 3rd Edition, Cambridge University Press, 2015.

• Gray, P. R., Hurst, P. J., Lewis, S. H., & Meyer, R. G.
  Analysis and Design of Analog Integrated Circuits, 5th Edition, Wiley, 2009.

• Sensitivity analysis in a resistive circuit with PySpice — Laboratory Pattern Recognition

• NgSpice Documentation — Open Source Circuit Simulator based on SPICE 3f5

• PySpice Documentation — Python Interface for NgSpice Simulation

• Shockley Diode Equation — Wikipedia, The Free Encyclopedia