
نام:
محمدحسین عصارنیا
وابستگی:
گروه مهندسی کامپیوتر، دانشگاه فردوسی مشهد
تماس:
m.hosein.assarnia@gmail.com
مبدلهای AC به DC که به یکسوکنندهها نیز معروف هستند، دستگاههای الکترونیکی هستند که جریان متناوب (AC) را به جریان مستقیم (DC) تبدیل میکنند. این تبدیل در بسیاری از سیستمهای الکتریکی و الکترونیکی حیاتی است، زیرا اکثر دستگاههای مدرن مانند رایانهها، تلفنهای هوشمند و تجهیزات صنعتی با برق DC کار میکنند. اهمیت مبدلهای AC به DC فراتر از لوازم الکترونیکی مصرفی کوچک، به کاربردهای در مقیاس بزرگ از جمله سیستمهای انرژی تجدیدپذیر، منبعهای تغذیه، خودروهای الکتریکی و زیرساختهای مخابراتی گسترش مییابد.
نیاز به تبدیل AC به DC در حوزههای متعددی گسترده است:

فصل 2: اصول بنیادی توان AC و DC
فصل 3: معماریها و اجزای منبع تغذیه
فصل 4: مدارهای یکسوکننده و تحلیل
فصل 5: تکنیکهای رگولاسیون و توپولوژیهای پیشرفته
فصل 6: طراحی و شبیهسازی مبدلهای AC به DC
فصل 7: کاربردهای صنعتی و پیشرفتهای فناوری در مبدلهای AC به DC
فصل 8: بررسی چالشها و مسائل در تبدیل AC به DC
نتیجهگیری
منابع
درک مفاهیم بنیادی توان جریان متناوب (AC) و جریان مستقیم (DC) برای تحلیل و طراحی سیستمهای الکتریکی و الکترونیکی ضروری است. این فصل اصول فیزیکی و ریاضی پشت توان AC و DC را بررسی میکند و پایهای علمی برای مطالعه مبدلهای AC به DC فراهم میآورد.
تعریف توان الکتریکی توان الکتریکی نرخ انتقال انرژی در طول زمان است و با واحد وات (W) اندازهگیری میشود. فرمول کلی برای توان به صورت زیر است:
\[P = V \times I\]که در آن:
جریان مستقیم (DC) در سیستمهای DC، ولتاژ و جریان در طول زمان ثابت میمانند. توان DC معمولاً توسط منابعی مانند باتریها و منبعهای تغذیه DC تأمین میشود. یک ویژگی کلیدی DC این است که انرژی را به صورت پیوسته و در یک جهت جریان میدهد.
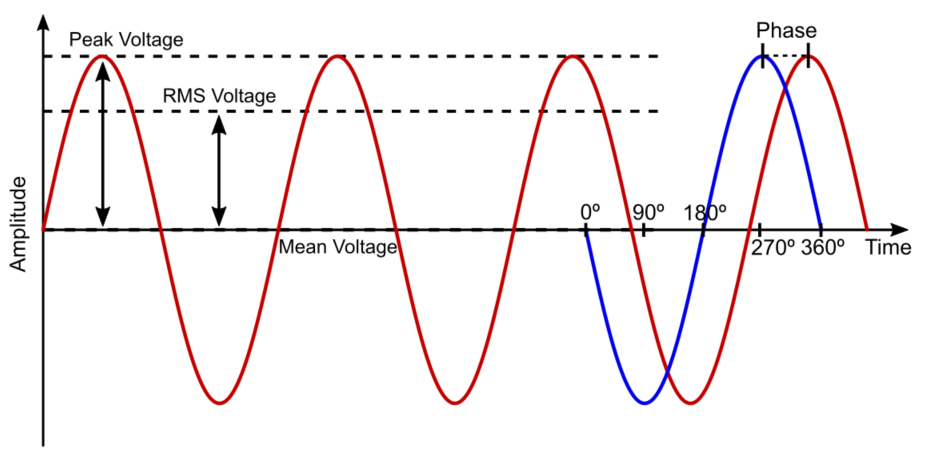
ویژگیهای جریان متناوب فرم موج معمول برای یک جریان متناوب، موج سینوسی است. هنگام کار با یک منبع تغذیه AC چندین شاخص باید در نظر گرفته شوند:
در اینجا مثالی از یک موج AC میبینیم:
مزایا و معایب منبع تغذیه DC
جریان مستقیم، که در آن برق همیشه در جهت ثابتی جریان دارد، مزایا و معایب زیر را دارد:
نمودار زیر یک دیاگرام از یک منبع ولتاژ DC را نشان میدهد:
from PySpice.Spice.Netlist import Circuit
from PySpice.Unit import *
import matplotlib.pyplot as plt
import numpy as np
# ایجاد یک مدار جدید
circuit = Circuit('DC Signal')
# تعریف یک منبع ولتاژ DC
circuit.V(1, 'n1', circuit.gnd, 5@u_V) # ولتاژ DC برابر 5 ولت
# شبیهسازی مدار
simulator = circuit.simulator(temperature=25, nominal_temperature=25)
analysis = simulator.operating_point()
# استخراج مقدار ولتاژ
voltage = float(analysis['n1'])
# آرایه زمانی برای رسم (0 تا 10 ثانیه)
time = np.linspace(0, 10, 1000)
# ایجاد یک آرایه با مقدار ولتاژ DC
dc_voltage = np.full_like(time, voltage)
# رسم سیگنال DC
plt.figure(figsize=(10, 5))
plt.plot(time, dc_voltage, label='ولتاژ DC', color='blue')
# افزودن برچسب و عنوان
plt.title('سیگنال DC')
plt.xlabel('زمان [ثانیه]')
plt.ylabel('ولتاژ [ولت]')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.legend()
plt.grid(True)
# نمایش نمودار
plt.show()
مزایا و معایب منبع تغذیه AC جریان متناوب، با ولتاژ مثبت و منفی چرخهای خود، مزایا و معایب زیر را دارد:
نمودار زیر یک AC سهفاز را نشان میدهد:
import matplotlib.pyplot as plt
import numpy as np
# متغیر زمان (0 تا 2π برای نمایش یک سیکل کامل)
t = np.linspace(0, 2 * np.pi, 1000)
# شکلموج سهفاز با جابجایی فاز 120 درجه
V1 = np.sin(t) # فاز A
V2 = np.sin(t - 2 * np.pi / 3) # فاز B (جابجایی 120 درجه)
V3 = np.sin(t - 4 * np.pi / 3) # فاز C (جابجایی 240 درجه)
# رسم شکلموجها
plt.figure(figsize=(10, 5))
plt.plot(t, V1, label='فاز A', color='red')
plt.plot(t, V2, label='فاز B', color='blue')
plt.plot(t, V3, label='فاز C', color='orange')
# افزودن برچسب و عنوان
plt.title('جریان متناوب سهفاز')
plt.xlabel('زمان [ثانیه]')
plt.ylabel('ولتاژ [ولت]')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.legend()
plt.grid(True)
# نمایش نمودار
plt.show()
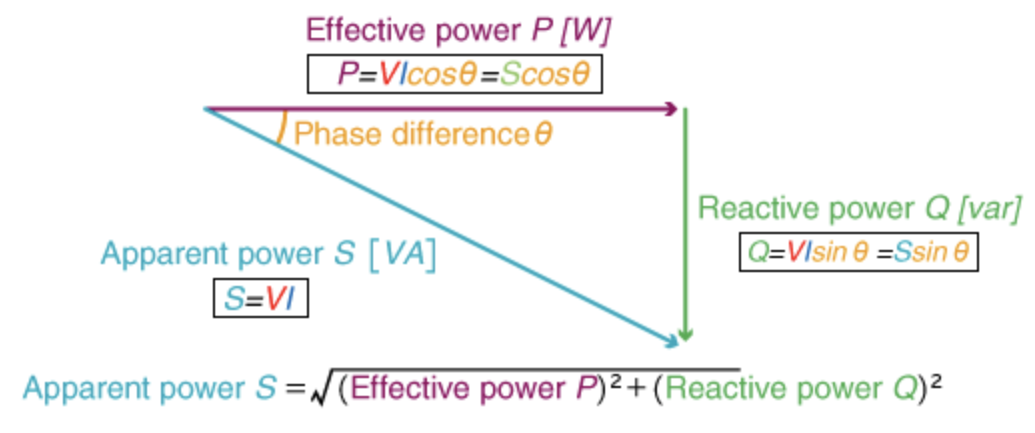
توان اکتیو و راکتیو در منابع AC
رابطه بین توان اکتیو، راکتیو و ظاهری را میتوان در تصاویر زیر مشاهده کرد:
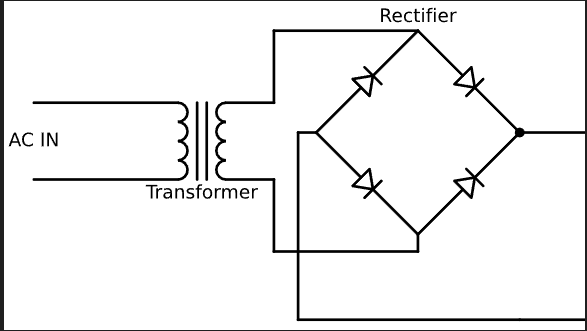
منبع تغذیه خطی AC/DC: یک منبع تغذیه خطی AC/DC طراحی سادهای دارد. اجزای یک منبع تغذیه خطی AC/DC شامل ترانسفورماتور، یکسوکننده و فیلتر است. با استفاده از یک ترانسفورماتور، ولتاژ ورودی جریان متناوب (AC) به مقداری مناسبتر برای کاربرد مورد نظر کاهش مییابد. سپس، ولتاژ AC کاهشیافته یکسو شده (یکسوکننده وسیلهای الکتریکی است که جریان متناوب (AC) را که دورهای جهت خود را معکوس میکند، به جریان مستقیم (DC) که فقط در یک جهت جریان دارد، تبدیل میکند) و به یک ولتاژ جریان مستقیم (DC) تبدیل میشود که برای بهبود بیشتر کیفیت شکل موج فیلتر میشود. فرآیند داخل یک منبع تغذیه خطی DC به صورت زیر توصیف میشود:
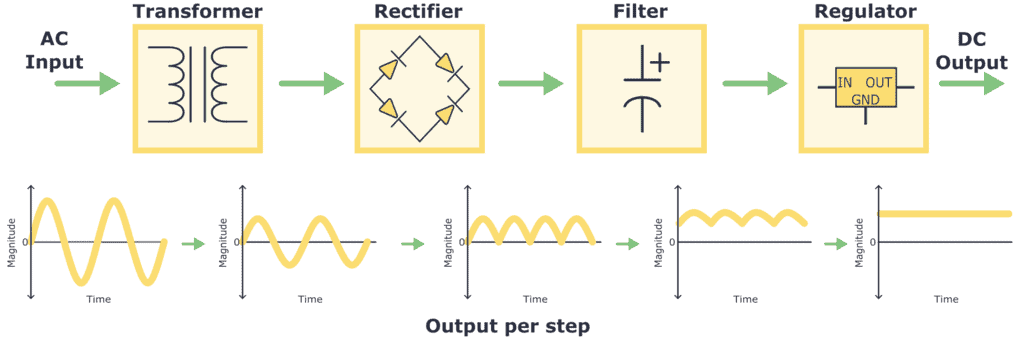
یک محدودیت بزرگ در یک منبع تغذیه خطی AC/DC، اندازه ترانسفورماتور است. از آنجا که ولتاژ ورودی در ورودی تبدیل میشود، ترانسفورماتور لازم باید بسیار بزرگ و در نتیجه بسیار سنگین باشد.
رسم یک منبع تغذیه خطی AC/DC با استفاده از schemdraw کد زیر یک منبع تغذیه خطی ساده را نشان میدهد:
import matplotlib.pyplot as plt
import schemdraw
import schemdraw.elements as elm
from schemdraw import dsp
with schemdraw.Drawing() as d:
d.push()
elm.Line()
tr = elm.Transformer().right().label('ترانسفورماتور', loc='bot').anchor('p1')
elm.Line().length(d.unit/3).at(tr.s1)
elm.Line().length(d.unit/2).up()
elm.Line().right()
rec = elm.Rectifier().anchor('N').label('یکسوکننده')
d.pop()
elm.Gap().toy(tr.p2).label(['', 'ورودی AC', ''])
elm.Line().tox(tr.p1)
elm.Line().length(d.unit/3).at(tr.s2)
elm.Line().length(d.unit/2).down()
elm.Line().right()
elm.Line().toy(rec.S)
elm.Line().length(d.unit/8).at(rec.W).left()
lineRec = elm.Line().length(d.unit*1.3).down()
lineOne = elm.Line().at(rec.E).right().idot()
line = elm.Line().idot()
lineTwo = elm.Line().length(d.unit/3)
lineThree = dsp.Square().label('رگولاتور')
lineFour = elm.Line().length(d.unit/3)
lineFive = elm.Line().length(d.unit/2)
elm.Gap().toy(lineRec.end).label(['+', 'خروجی DC', '–'])
lineFiveEnd = elm.Line().length(d.unit/2).left()
lineThreeEnd = elm.Line().tox(lineThree.S)
lineTwoEnd = elm.Line().tox(lineTwo.start)
lineEnd = elm.Line().tox(line.start).dot()
lineOneEnd = elm.Line().tox(lineOne.start)
elm.Line().tox(lineRec.end)
elm.Capacitor().endpoints(lineOne.end,lineOneEnd.start).label('فیلتر')
elm.Capacitor().endpoints(lineTwo.start,lineEnd.start).label('C1')
elm.Line().endpoints(lineTwoEnd.start,lineThree.S)
elm.Capacitor().endpoints(lineFive.start,lineFiveEnd.end).label('C2')
plt.show()
منبع تغذیه سوئیچینگ AC/DC: رویکرد طراحی جدیدی برای حل بسیاری از مشکلات مرتبط با طراحی منبع تغذیه خطی یا سنتی AC/DC، از جمله اندازه ترانسفورماتور و تنظیم ولتاژ، توسعه یافته است. منابع تغذیه سوئیچینگ اکنون به لطف تکثیر فناوری نیمههادی، به ویژه به دلیل ایجاد ترانزیستورهای MOSFET پرتوان که میتوانند بسیار سریع و کارآمد روشن و خاموش شوند، حتی در حضور ولتاژها و جریانهای بزرگ، امکانپذیر شدهاند. یک منبع تغذیه سوئیچینگ AC/DC امکان ایجاد مبدلهای توان کارآمدتر را فراهم میکند که دیگر توان اضافی را تلف نمیکنند.
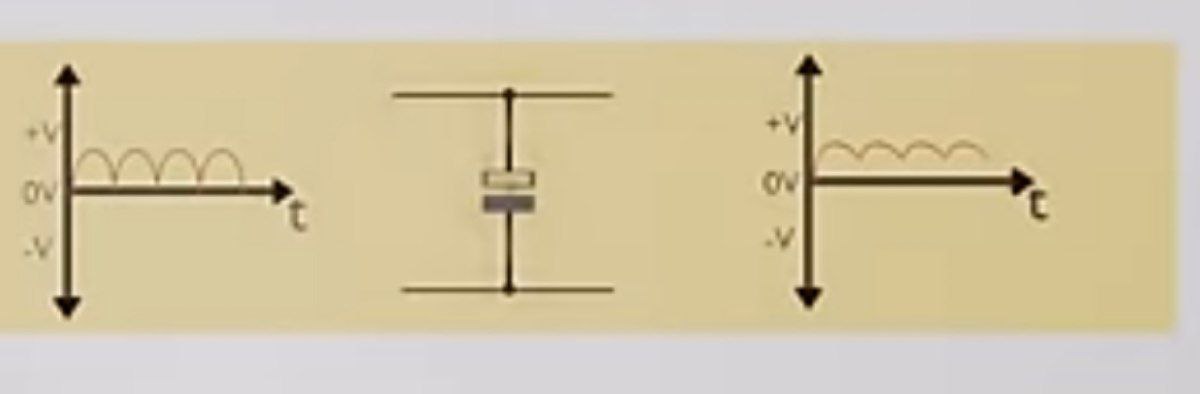
در منابع تغذیه سوئیچینگ AC، ولتاژ ورودی دیگر کاهش نمییابد؛ بلکه در ورودی یکسو و فیلتر میشود. سپس ولتاژ DC از طریق یک چاپر (Chopper) میگذرد که ولتاژ را به یک قطار پالس با فرکانس بالا تبدیل میکند. در نهایت، موج از طریق یک یکسوکننده و فیلتر دیگر عبور میکند که آن را دوباره به جریان مستقیم (DC) تبدیل کرده و هر جزء جریان متناوب (AC) باقیمانده قبل از رسیدن به خروجی را حذف میکند. فرآیند به صورت زیر نشان داده شده است:
اگرچه مدارهای سوئیچینگ مختلف زیادی وجود دارد، اما رایجترین آنها PWM (مدولاسیون عرض پالس) است. شکل زیر یک بلوک دیاگرام پایه از رگولاتور سوئیچینگ PWM است. این مدار سطح ولتاژ را به شکل حلقه بسته حفظ میکند:
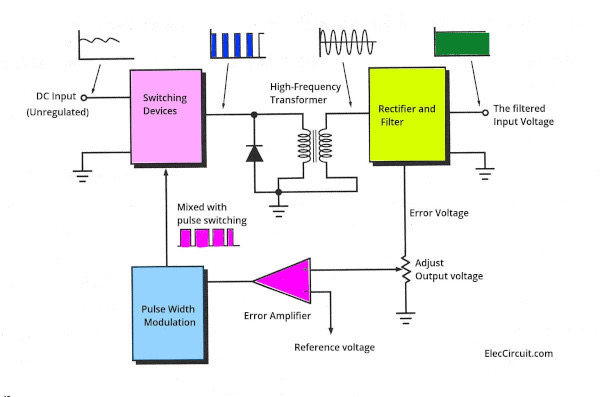
ترانسفورماتورهای کوچکتر و افزایش راندمان رگولاتور ولتاژ در منابع تغذیه سوئیچینگ AC/DC دلیل این است که اکنون میتوانیم یک ولتاژ AC 220 ولت RMS را به یک ولتاژ DC 5 ولت با یک مبدل توان که در کف دست جا میگیرد تبدیل کنیم.
1. ترانسفورماتور
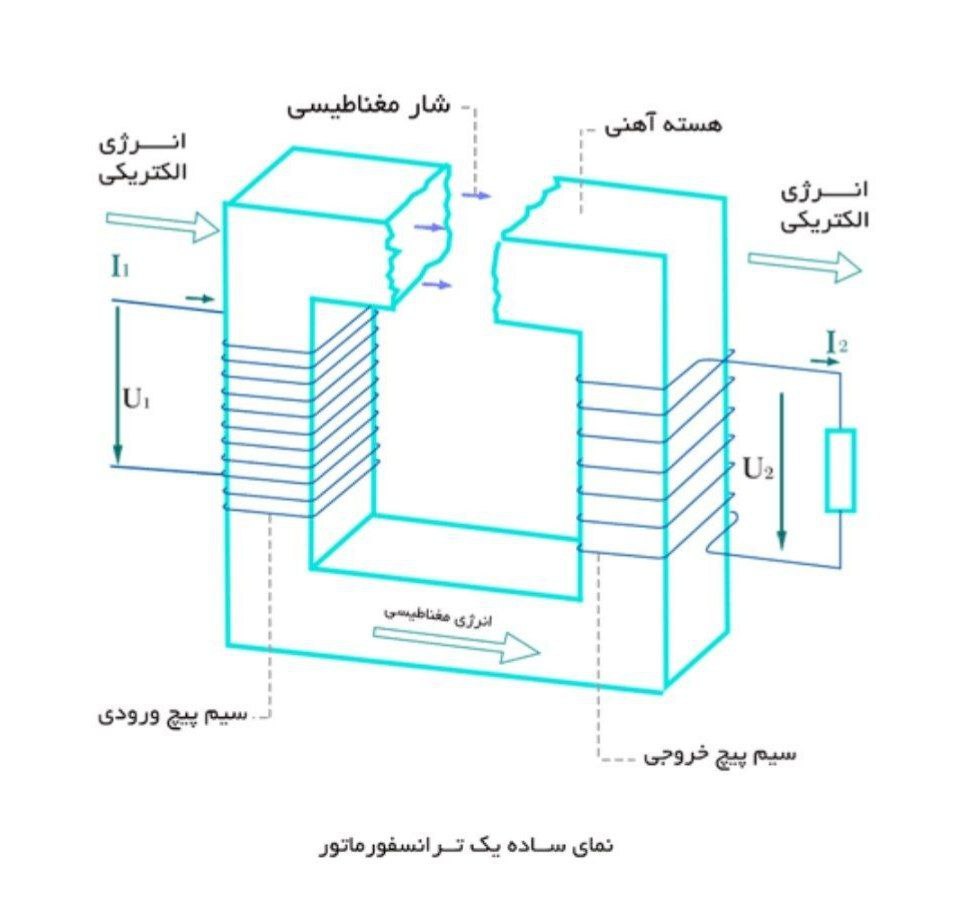

2. مدار یکسوکننده
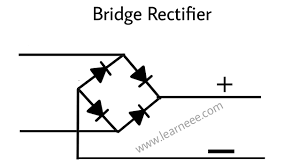
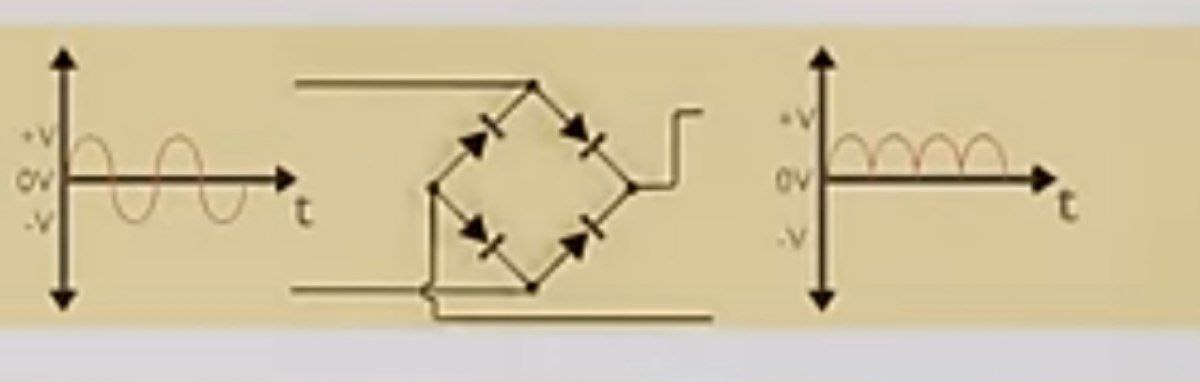
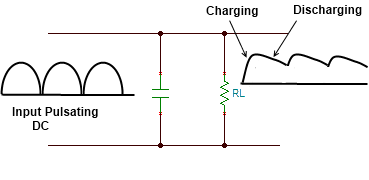
3. فیلتر (خازن / سلف)
4. تنظیمکننده ولتاژ (رگولاتور)


یک منبع تغذیه جریان متناوب (AC) میتواند تکفاز یا سهفاز باشد:
دو پیکربندی برای انتقال توان از طریق یک منبع تغذیه سهفاز وجود دارد: پیکربندی مثلث (Δ) و ستاره (Y). تفاوت اصلی بین این دو پیکربندی، امکان افزودن یک سیم نول است. اتصالات مثلث قابلیت اطمینان بیشتری ارائه میدهند، اما اتصالات ستاره میتوانند دو ولتاژ مختلف را تأمین کنند: ولتاژ فاز که ولتاژ تکفاز تأمینشده به خانهها است و ولتاژ خط برای تأمین توان بارهای بزرگتر. در پیکربندی مثلث، ولتاژ فاز برابر با ولتاژ خط است در حالی که در پیکربندی ستاره، ولتاژ فاز برابر ولتاژ خط تقسیم بر ریشه 3 است. پیکربندیهای ستاره معمولاً برای سیستمهایی استفاده میشوند که به نول نیاز است، مانند شبکههای توزیع برای ساختمانهای مسکونی یا تجاری، زیرا اجازه خروجیهای هم 120 ولت و هم 240 ولت را میدهند. پیکربندیهای مثلث اغلب در محیطهای صنعتی که توان بالا مورد نیاز است و نیازی به نول نیست، مانند موتورها و ماشینآلات سنگین استفاده میشوند.
تصویر زیر نشان میدهد که سیمها در پیکربندیهای ستاره و مثلث چگونه متصل میشوند:
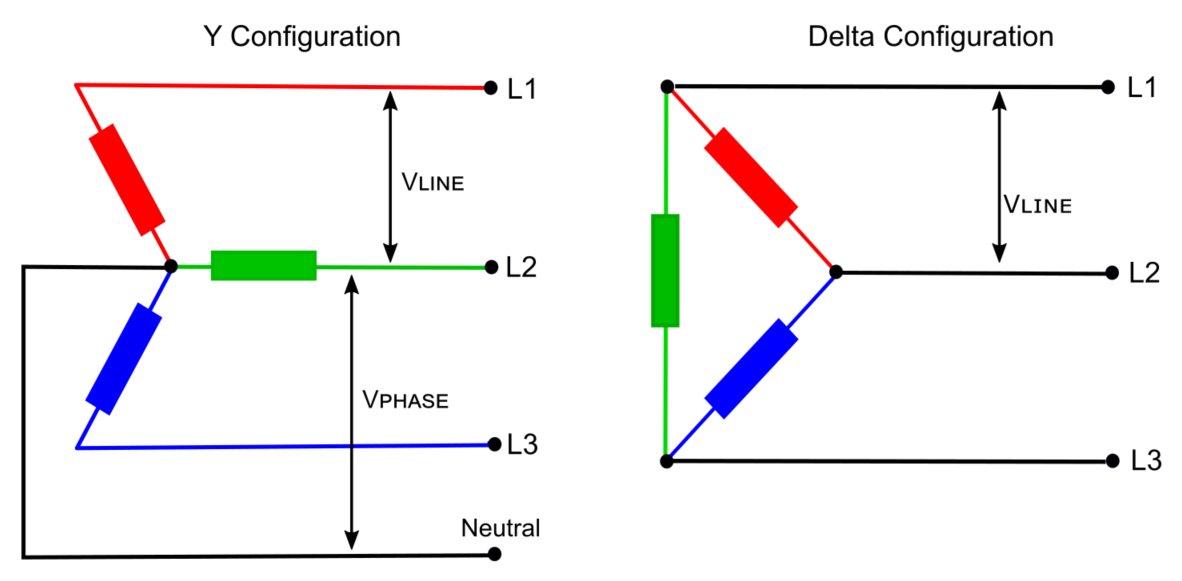
همانطور که قبلاً ذکر شد، توان سهفاز نه تنها برای انتقال استفاده میشود، بلکه برای تأمین توان بارهای بزرگ، مانند موتورهای الکتریکی یا شارژ باتریهای بزرگ نیز استفاده میشود. این به این دلیل است که اعمال موازی توان در سیستمهای سهفاز میتواند انرژی بسیار بیشتری را به یک بار منتقل کند و به دلیل همپوشانی سه فاز، میتواند این کار را به طور یکنواختتری انجام دهد. به عنوان مثال، هنگام شارژ یک وسیله نقلیه الکتریکی (EV)، مقدار توانی که میتوان به باتری منتقل کرد، سرعت شارژ آن را تعیین میکند. شارژرهای تکفاز به برق متناوب (AC) اصلی متصل شده و توسط مبدل AC/DC داخلی خودرو (که همچنین به عنوان شارژر داخلی شناخته میشود) به جریان مستقیم (DC) تبدیل میشوند. این شارژرها توسط شبکه و پریز AC از نظر توان محدود میشوند.
تصویر زیر انتقال توان در سیستمهای تکفاز و سهفاز را نشان میدهد:
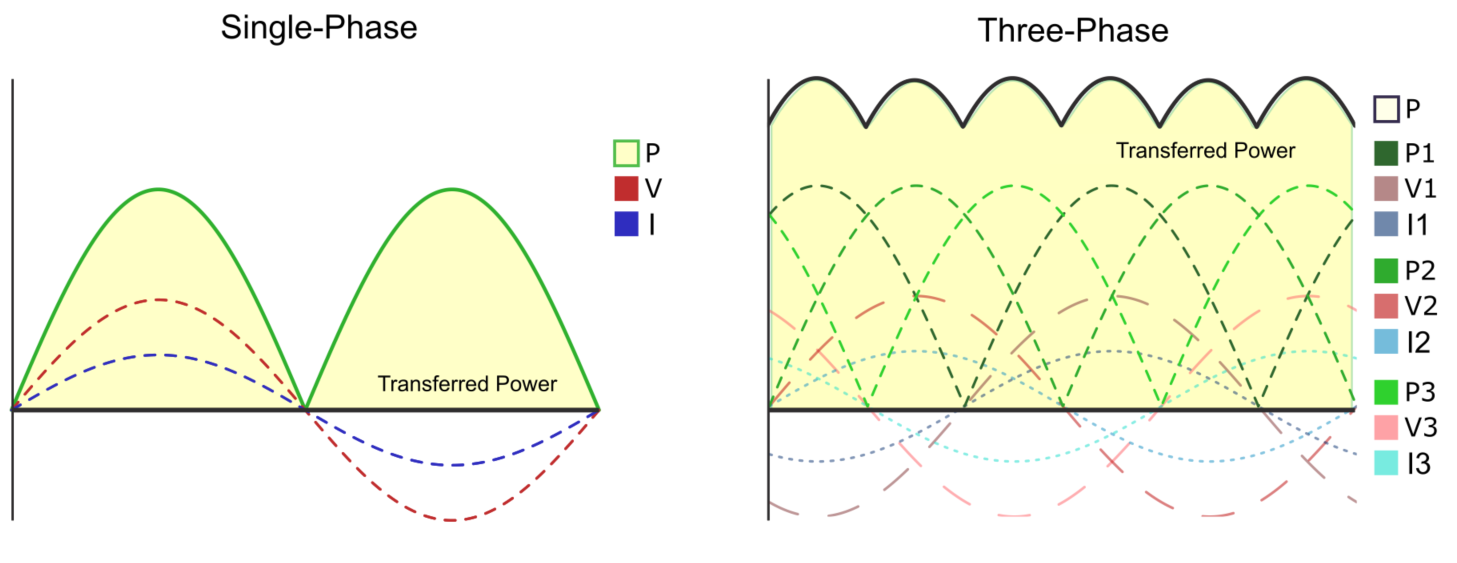
این مثال محاسبه ولتاژ برای پیکربندیهای ستاره و مثلث را نشان میدهد. بیایید از یک شبکه الکتریکی 220 ولت / 50 هرتز استفاده کنیم. ولتاژهای فاز در پیکربندی ستاره به اندازه $\frac{2\pi}{3}$ از هم فاصله دارند:
\(V_{L1-N} = V_{pp} \cos(\omega t)\) \(V_{L2-N} = V_{pp} \cos(\omega t - \frac{2\pi}{3})\) \(V_{L3-N} = V_{pp} \cos(\omega t - \frac{4\pi}{3})\)
آنها را به صورت مختلط بازنویسی میکنیم: \(V_{L1-N} = V_{pp} e^{j\omega t}\) \(V_{L2-N} = V_{pp} e^{j(\omega t - \frac{2\pi}{3})}\) \(V_{L3-N} = V_{pp} e^{j(\omega t - \frac{4\pi}{3})}\)
از این عبارات، ولتاژ در پیکربندی مثلث را با استفاده از روابط مثلثاتی محاسبه میکنیم:
\(V_{L1-L2} = V_{L1} \sqrt{3}\ e^{j\frac{\pi}{6}}\) \(V_{L2-L3} = V_{L2} \sqrt{3}\ e^{j\frac{\pi}{6}}\) \(V_{L3-L1} = V_{L3} \sqrt{3}\ e^{j\frac{\pi}{6}}\)
در مقایسه با پیکربندی ستاره، ولتاژها در پیکربندی مثلث توسط ضریب $\sqrt{3}$ بزرگ شده و به اندازه $\frac{\pi}{6}$ جابجایی فاز دارند.
در نهایت آنها را به صورت زمانی بازنویسی میکنیم:
\(V_{L1-L2} = V_{pp} \sqrt{3} \cos(\omega t + \frac{\pi}{6})\) \(V_{L2-L3} = V_{pp} \sqrt{3} \cos(\omega t - \frac{\pi}{2})\) \(V_{L3-L1} = V_{pp} \sqrt{3} \cos(\omega t - \frac{7\pi}{6})\)
حال شکلموجها را رسم میکنیم:
import math
import numpy as np
import matplotlib.pyplot as plt
from PySpice.Unit import *
frequency = 50@u_Hz
w = frequency.pulsation
period = frequency.period
rms_mono = 220
amplitude_mono = rms_mono * math.sqrt(2)
t = np.linspace(0, 3*float(period), 1000)
## پیکربندی ستاره
L1 = amplitude_mono * np.cos(t*w) ## فاز یک
L2 = amplitude_mono * np.cos(t*w - 2*math.pi/3) ## فاز دو
L3 = amplitude_mono * np.cos(t*w - 4*math.pi/3) ## فاز سه
rms_tri = math.sqrt(3) * rms_mono
amplitude_tri = rms_tri * math.sqrt(2)
## پیکربندی مثلث
L12 = amplitude_tri * np.cos(t*w + math.pi/6)
L23 = amplitude_tri * np.cos(t*w - math.pi/2)
L31 = amplitude_tri * np.cos(t*w - 7*math.pi/6)
figure, ax = plt.subplots(figsize=(20, 10))
ax.plot(
t, L1, t, L2, t, L3,
t, L12, t, L23, t, L31,
# t, L1-L2, t, L2-L3, t, L3-L1,
)
ax.grid()
ax.set_title('توان الکتریکی سهفاز: پیکربندیهای ستاره و مثلث (220V تکفاز / 400V سهفاز 50Hz ایران)')
ax.legend(
('L1-N', 'L2-N', 'L3-N',
'L1-L2', 'L2-L3', 'L3-L1'),
loc=(.7,.5),
)
ax.set_xlabel('زمان [ثانیه]')
ax.set_ylabel('[ولت]')
ax.axhline(y=rms_mono, color='blue')
ax.axhline(y=-rms_mono, color='blue')
ax.axhline(y=rms_tri, color='blue')
ax.axhline(y=-rms_tri, color='blue')
plt.show()
یک یکسوکننده نیمموج با مسدود کردن یک نیمه از شکل موج، با استفاده از یک دیود، AC را به DC تبدیل میکند و در مقایسه با یکسوکننده تمامموج کارایی کمتری دارد. یک یکسوکننده تمامموج، مانند پل یکسوکننده تمامموج با چهار دیود، کل شکل موج را به DC تبدیل میکند و خروجی هموارتری ارائه میدهد.
دیودهای توان را میتوان به صورت جداگانه مانند زیر استفاده کرد یا به هم متصل کرد تا انواع مختلفی از مدارهای یکسوکننده تولید شوند.

در بسیاری از کاربردها، ولتاژ پیک را با استفاده از یک ترانسفورماتور قبل از اعمال آن به یک یکسوکننده نیمموج کاهش میدهیم.
در طول نیمسیکل مثبت موج سینوسی AC، دیود بایاس مستقیم اجازه میدهد جریان جاری شود و ولتاژ خروجی را برابر ولتاژ منبع منهای ولتاژ مستقیم دیود میکند. در نیمسیکل منفی، دیود بایاس معکوس جریان را مسدود میکند و در نتیجه ولتاژ خروجی صفر میشود.
سمت DC مدار یکسو است و مقاومت بار یک شکل موج ولتاژ نامنظم متشکل از ولتاژهای مثبت و صفر دریافت میکند. این ولتاژ معادل $ 0.318 * V_\text{max} $ یا $ 0.45 * V_\text{rms} $ شکل موج سینوسی ورودی است.
محاسبه مقدار DC خروجی
\[V_{\text{avg}} = \frac{1}{T} \int_{0}^{T} v(t) \, dt\]برای یک شکل موج سینوسی یکسو شده نیمموج، باید میانگین را در یک دوره در نظر بگیریم، اما چون شکل موج یکسو شده است، برای نیمی از دوره صفر است. بنابراین، میانگین را روی نیمسیکل غیرصفر محاسبه کرده و سپس از فرمول برای دوره کامل استفاده میکنیم.
شکل موج $ v(t) = V_{\text{max}} \sin(\omega t) $ برای $0 \leq t < T/2$ و صفر برای $ T/2 \leq t < T $.
مقدار متوسط در طول دوره برابر است با:
\[V_{\text{avg}} = \frac{1}{T} \int_{0}^{T} v(t) \, dt\]از آنجا که $ v(t) = V_{\text{max}} \sin(\omega t) $ از $0$ تا $T/2$ و $0$ از $T/2$ تا $T$:
\[V_{\text{avg}} = \frac{1}{T} \left( \int_{0}^{T/2} V_{\text{max}} \sin(\omega t) \, dt \right)\]انتگرال را محاسبه میکنیم:
\[\int_{0}^{T/2} V_{\text{max}} \sin(\omega t) \, dt = \frac{V_{\text{max}}}{\omega} \left[ -\cos(\omega t) \right]_{0}^{T/2}\]با جایگذاری حدود:
\[\frac{V_{\text{max}}}{\omega} \left[ -\cos\left(\frac{\omega T}{2}\right) + \cos(0) \right]\]از آنجا که $\cos\left(\frac{\omega T}{2}\right) = \cos(\pi) = -1$ و $\cos(0) = 1$:
\[\frac{V_{\text{max}}}{\omega} \left[ -(-1) + 1 \right] = \frac{V_{\text{max}}}{\omega} \cdot 2\]بنابراین:
\[\frac{1}{T} \cdot \frac{V_{\text{max}} \cdot 2}{\omega}\]از آنجا که $\omega = \frac{2\pi}{T}$:
\[\frac{1}{T} \cdot \frac{2 V_{\text{max}} T}{2 \pi} = \frac{2 V_{\text{max}}}{2 \pi} = \frac{V_{\text{max}}}{\pi}\]بنابراین، مقدار متوسط صحیح $ V_{\text{avg}} $ برابر است با:
\[V_{\text{DC}} = V_{\text{avg}} = \frac{V_{\text{max}}}{\pi} = 0.318V_{\text{max}}\]همچنین مینویسیم $ V_{\text{rms}} $ بر حسب $ V_{\text{max}} $:
\[V_{\text{rms}} = \frac{V_{\text{max}}}{\sqrt{2}}\]$ V_{\text{max}} $ را بر حسب $ V_{\text{DC}} $ بیان میکنیم:
با توجه به $ V_{\text{DC}} = \frac{V_{\text{max}}}{\pi} $،
\[V_{\text{max}} = \pi \times V_{\text{DC}}\]$ V_{\text{max}} $ را در فرمول $ V_{\text{rms}} $ جایگزین میکنیم:
\[V_{\text{rms}} = \frac{\pi \times V_{\text{DC}}}{\sqrt{2}}\]عبارت را ساده میکنیم:
\[V_{\text{rms}} = \pi \times \frac{V_{\text{DC}}}{\sqrt{2}}\]بنابراین،
\[V_{\text{DC}} \approx 0.45 \times V_{\text{rms}}\]تذکر: برای یافتن $ V_{\text{rms}} $ سیگنال سینوسی ورودی در یک دوره و سپس ارتباط آن با $ V_{\text{DC}} $، باید مقدار RMS را برای کل دوره سیگنال ورودی محاسبه کنیم.
مقدار RMS سیگنال سینوسی ورودی:
سیگنال سینوسی ورودی $ v(t) = V_{\text{max}} \sin(\omega t) $ در طول یک دوره $ T $ مقدار RMS زیر را دارد:
\[V_{\text{rms}} = \sqrt{\frac{1}{T} \int_0^T \left(V_{\text{max}} \sin(\omega t)\right)^2 \, dt}\] \[V_{\text{rms}} = V_{\text{max}} \sqrt{\frac{1}{T} \int_0^T \sin^2(\omega t) \, dt}\]با استفاده از اتحاد $ \sin^2(x) = \frac{1 - \cos(2x)}{2} $:
\[\sin^2(\omega t) = \frac{1 - \cos(2\omega t)}{2}\]بنابراین،
\[V_{\text{rms}} = V_{\text{max}} \sqrt{\frac{1}{T} \int_0^T \frac{1 - \cos(2\omega t)}{2} \, dt}\] \[V_{\text{rms}} = V_{\text{max}} \sqrt{\frac{1}{T} \cdot \frac{1}{2} \int_0^T (1 - \cos(2\omega t)) \, dt}\]انتگرال $ 1 $ روی $ 0 $ تا $ T $ برابر $ T $ است و انتگرال $ \cos(2\omega t) $ روی یک دوره $ T $ برابر صفر است:
\[\int_0^T 1 \, dt = T\] \[\int_0^T \cos(2\omega t) \, dt = 0\]بنابراین،
\[V_{\text{rms}} = \frac{V_{\text{max}}}{\sqrt{2}}\]یکسوکننده تمامموج دیودهای توان را میتوان به هم متصل کرد تا یک یکسوکننده تمامموج تشکیل دهند که ولتاژ AC را به ولتاژ DC برای منابع تغذیه تبدیل میکند. این یکسوکننده از چهار دیود برای تبدیل هر دو نیمه از هر سیکل شکل موج AC به یک سیگنال DC استفاده میکند. در حالی که خازنهای هموارکننده میتوانند ریپل را برای کاربردهای کمتوان کاهش دهند، یک یکسوکننده تمامموج برای نیازهای توان بالاتر کارآمدتر است و از هر نیمسیکل ولتاژ ورودی استفاده میکند.
نحوه کار
نیمسیکل مثبت
نیمسیکل منفی
مزایا و عملکرد مدار یک یکسوکننده تمامموج ولتاژ DC خروجی متوسط بالاتری با ریپل کمتر در مقایسه با یک یکسوکننده نیمموج تولید میکند که منجر به شکل موج خروجی هموارتری میشود. مانند یکسوکننده نیمموج، میتواند به موارد زیر برسد:
یک یکسوکننده تمامموج کل شکل موج AC را به DC تبدیل میکند و خروجی هموارتر و کارآمدتری نسبت به یک یکسوکننده نیمموج ارائه میدهد. این یکسوکننده از چهار دیود برای یکسو کردن هر دو نیمه سیکل AC استفاده میکند که منجر به خروجی DC متوسط بالاتر با ریپل کاهشیافته میشود.
دیودهای توان را میتوان در پیکربندیهای مختلف مدارهای یکسوکننده قرار داد. یک طراحی رایج، یکسوکننده تمامموج با استفاده از یک ترانسفورماتور تپ مرکزی و دو دیود برای مدیریت هر دو نیمسیکل شکل موج ورودی است. این پیکربندی فرکانس سیگنال خروجی را دو برابر میکند که منجر به خروجی DC هموارتر میشود.
محاسبه مقدار DC خروجی برای یک یکسوکننده تمامموج، ولتاژ DC متوسط خروجی $V_{\text{DC}}$ به صورت زیر داده میشود:
\[V_{\text{DC}} = \frac{2 V_{\text{max}}}{\pi}\]که در آن $ V_{\text{max}} $ مقدار پیک سیگنال AC است. این نتیجه نشان میدهد که ولتاژ DC خروجی در مقایسه با یک یکسوکننده نیمموج بالاتر و هموارتر است.
مدار از دو دیود و یک ترانسفورماتور تپ مرکزی استفاده میکند که به هر دیود اجازه میدهد در طول نیمسیکلهای مخالف هدایت کند. این پیکربندی فرکانس خروجی را دو برابر میکند و یکسوکننده تمامموج را 100٪ کارآمد میسازد. جهت جریان ثابت از طریق مقاومت بار در طول هر دو نیمسیکل، یک خروجی DC پیوسته را تضمین میکند.
خازنها خروجی یکسوکننده تمامموج را هموار میکنند و ریپل پیک تو پیک را برای یک ولتاژ پایدارتر کاهش میدهند.
ریپل جزء AC باقیمانده در خروجی یک یکسوکننده نیمموج است که باعث میشود شکل موج DC ضربانی شود. ضریب ریپل $ \gamma $ این جزء AC ناخواسته را کمّی میکند و به صورت زیر به دست میآید:
\[\gamma = \frac{\text{مقدار RMS جزء AC}}{\text{مقدار جزء DC}} = \frac{V_{r(\text{rms})}}{V_{dc}}.\] \[\gamma = \sqrt{\frac{V_{rms}^2}{V_{dc}^2} - 1}.\]اثبات: در اینجا، $ V_{r(\text{rms})} $ نشاندهنده مقدار RMS جزء AC و $ V_{dc} $ جزء DC خروجی است.
برای تعیین $ V_{r(\text{rms})} $، با بیان ولتاژ خروجی یکسوکننده نیمموج شروع میکنیم:
\[V_o(t) = V_{ac} + V_{dc},\]که در آن $ V_{ac} $ جزء AC باقیمانده پس از یکسوسازی است. مقدار RMS جزء AC را میتوان با استفاده از فرمول زیر محاسبه کرد:
\[V_{r(\text{rms})} = \left( \frac{1}{T} \int_0^T V_{ac}^2 \, dt \right)^{1/2}.\]همچنین میتوانیم $ V_{r(\text{rms})} $ را به صورت زیر بنویسیم:
\[V_{r(\text{rms})}^2 = \frac{1}{T} \int_0^T (V_o - V_{dc})^2 \, dt.\]با بسط مربع و انتگرالگیری، به دست میآوریم:
\[V_{r(\text{rms})}^2 = \frac{1}{T} \int_0^T (V_o^2 - 2V_o V_{dc} + V_{dc}^2) \, dt.\]این عبارت به صورت زیر ساده میشود:
\[V_{r(\text{rms})}^2 = \frac{1}{T} \int_0^T V_o^2 \, dt - \frac{2V_{dc}}{T} \int_0^T V_o \, dt + V_{dc}^2.\]از آنجا که $ \frac{1}{T} \int_0^T V_o \, dt = V_{dc} $، داریم:
\[V_{r(\text{rms})}^2 = V_{rms}^2 - V_{dc}^2,\]که در آن $ V_{rms} $ مقدار RMS کل سیگنال ولتاژ است.
بنابراین، ضریب ریپل $ \gamma $ را میتوان به صورت زیر نوشت:
\[\gamma = \sqrt{\frac{V_{rms}^2}{V_{dc}^2} - 1}.\]با جایگذاری مقادیر $ V_{dc} $ و $ V_{rms} $، مییابیم:
\[\gamma = \sqrt{\frac{V_m^2 / 2 \cdot \pi}{V_m / \pi}^2 - 1} = \sqrt{\left(\frac{\pi}{2}\right)^2 - 1} \approx 1.21.\]ضریب ریپل یک یکسوکننده تمامموج ضریب ریپل ($ \gamma $) برای یک یکسوکننده تمامموج به صورت زیر تعریف میشود:
\[\gamma = \frac{V_{r(\text{rms})}}{V_{dc}} = \sqrt{\frac{V_{rms}^2}{V_{dc}^2} - 1},\]که در آن $ V_{r(\text{rms})} $ مقدار RMS جزء AC و $ V_{dc} $ جزء DC است. برای یک یکسوکننده تمامموج، ضریب ریپل به صورت زیر ساده میشود:
\[\gamma = \sqrt{\left(\frac{\pi}{2\sqrt{2}}\right)^2 - 1} \approx 0.48.\]یک چندبرابرکننده ولتاژ یک مدار الکتریکی است که توان الکتریکی AC را از یک ولتاژ پایینتر به یک ولتاژ DC بالاتر تبدیل میکند، معمولاً با استفاده از شبکهای از خازنها و دیودها. چندبرابرکنندههای ولتاژ میتوانند برای تولید چند ولت برای لوازم الکترونیکی تا میلیونها ولت استفاده شوند.
مثال $ V_o $ برابر با چهار برابر پیک ولتاژ ورودی AC $ V_i $
پس از یکسوسازی، خروجی DC را میتوان با استفاده از رگولاتورهاتثبیت کرد که عمدتاً دو نوع هستند:
یک رگولاتور ترانزیستوری ساده، ولتاژ خروجی نسبتاً ثابتی (Uout) را علیرغم تغییرات ولتاژ ورودی (Uin) و مقاومت بار (RL) حفظ میکند، مشروط بر اینکه Uin به اندازه کافی از Uout بیشتر باشد و ظرفیت توان ترانزیستور فراتر نرود. ولتاژ خروجی تثبیتکننده برابر است با ولتاژ دیود زنر منهای ولتاژ بیس-امیتر ترانزیستور (UZ − UBE)، که UBE به طور معمول حدود 0.7 ولت برای ترانزیستورهای سیلیکونی است. اگر Uout به دلیل عوامل خارجی کاهش یابد، UBE افزایش مییابد و ترانزیستور را بیشتر فعال میکند تا ولتاژ بار را افزایش دهد. Rv جریان بایاس را به هر دو دیود زنر و ترانزیستور تأمین میکند و مقدار آن بر نیازهای ولتاژ ورودی و کارایی رگولاتور تأثیر میگذارد. مقادیر کمتر Rv تلفات توان دیود را افزایش میدهد و عملکرد رگولاتور را بدتر میکند.
رگولاتور با یک تقویت کننده تفاضلی پایداری ولتاژ خروجی را میتوان با استفاده از یک تقویت کننده تفاضلی، مانند یک تقویت کننده عملیاتی، افزایش داد. این مدار جریان ترانزیستور را بر اساس اختلاف ولتاژ ورودی تنظیم میکند و اجازه میدهد ولتاژ خروجی قابل تنظیمی از طریق یک تقسیمکننده ولتاژ داشته باشیم.
نمونهای از رگولاتور خطی LM317 است: رگولاتور ولتاژ مثبت قابل تنظیم 1.5 آمپر (1.25 ولت تا 37 ولت)
import matplotlib.pyplot as plt
import schemdraw
import schemdraw.elements as elm
from schemdraw import dsp
with schemdraw.Drawing() as d:
d.push()
elm.Line()
tr = elm.Transformer().right().label('ترانسفورماتور', loc='bot').anchor('p1')
elm.Line().length(d.unit/3).at(tr.s1)
elm.Line().length(d.unit/2).up()
elm.Line().right()
rec = elm.Rectifier().anchor('N').label('یکسوکننده')
d.pop()
elm.Gap().toy(tr.p2).label(['', 'ورودی AC', ''])
elm.Line().tox(tr.p1)
elm.Line().length(d.unit/3).at(tr.s2)
elm.Line().length(d.unit/2).down()
elm.Line().right()
elm.Line().toy(rec.S)
elm.Line().length(d.unit/8).at(rec.W).left()
lineRec = elm.Line().length(d.unit*1.3).down()
lineOne = elm.Line().at(rec.E).right().idot()
line = elm.Line().idot()
lineTwo = elm.Line().length(d.unit/3)
lineThree = dsp.Square().label('رگولاتور')
lineFour = elm.Line().length(d.unit/3)
lineFive = elm.Line().length(d.unit/2)
elm.Gap().toy(lineRec.end).label(['+', 'خروجی DC', '–'])
lineFiveEnd = elm.Line().length(d.unit/2).left()
lineThreeEnd = elm.Line().tox(lineThree.S)
lineTwoEnd = elm.Line().tox(lineTwo.start)
lineEnd = elm.Line().tox(line.start).dot()
lineOneEnd = elm.Line().tox(lineOne.start)
elm.Line().tox(lineRec.end)
elm.Capacitor().endpoints(lineOne.end,lineOneEnd.start).label('فیلتر')
elm.Line().endpoints(lineTwoEnd.start,lineThree.S)
plt.show()
مبدلهای AC به DC نه تنها در مدارهای الکترونیکی کوچک بنیادی هستند، بلکه در بسیاری از سیستمهای صنعتی نیز نقش حیاتی ایفا میکنند. توانایی آنها در تبدیل جریان متناوب (AC) به جریان مستقیم (DC)، آنها را در سیستمهای قدرت، فرآیندهای تولید و فناوریهای مدرن ضروری میسازد.
کاربردهای صنعتی
الکترونیک مصرفی و مخابرات: تقریباً همه دستگاههای الکترونیکی مدرن – از رایانهها گرفته تا تلفنهای هوشمند – به ولتاژ DC نیاز دارند که از طریق مبدلهای برق AC/DC تأمین میشود.
صنعت خودرو: وسایل نقلیه الکتریکی و هیبریدی از مبدلهای AC به DC برای شارژ باتریها و تأمین انرژی سیستمهای الکترونیکی داخلی استفاده میکنند.
سیستمهای کنترل و اتوماسیون: در اتوماسیون صنعتی، دستگاههایی مانند PLCها، سنسورها و درایوهای موتور با برق DC کار میکنند. مبدلها ولتاژ پایدار را برای این سیستمهای کنترل فراهم میکنند.
منابع تغذیه صنعتی: منبع تغذیه سوئیچ-مود (SMPS) در کاربردهای صنعتی به تبدیل کارآمد AC به DC برای عملیات با کارایی بالا و صرفهجویی در انرژی متکی هستند.
پیشرفتهای فناوری
توسعههای فناوری اخیر به طور قابل توجهی عملکرد مبدلهای AC به DC را بهبود بخشیده است:
مواد نیمههادی پیشرفته (SiC, GaN): از این مواد برای ساخت دستگاههای توان سریعتر و کارآمدتر با تلفات کمتر استفاده میشود.
طراحیهای با کارایی بالا و فشرده: مبدلهای مدرن به گونهای طراحی شدهاند که کوچکتر، سبکتر و کارآمدتر باشند و از توپولوژیها و روشهای کنترل پیشرفته استفاده میکنند.
کنترل دیجیتال و ویژگیهای هوشمند: یکپارچهسازی میکروکنترلرها و پردازش سیگنال دیجیتال، تنظیم هوشمندتر و دقیقتر ولتاژ و جریان خروجی را ممکن میسازد.
در حالی که مبدلهای AC به DC در کاربردهای مختلف ضروری هستند، طراحی و عملکرد آنها با چندین چالش مواجه است. این مسائل از مشکلات فنی و مرتبط با طراحی گرفته تا نگرانیهای کارایی و خطرات ایمنی گسترده است.
چالشهای فنی
ریپل ولتاژ: حتی پس از یکسوسازی، ولتاژ DC خروجی کاملاً هموار نیست. ریپل میتواند باعث ناپایداری یا خرابی در مدارهای الکترونیکی حساس شود.
افت ولتاژ در دیودها: هر دیود یک افت ولتاژ مستقیم دارد (معمولاً ~0.7V برای دیودهای سیلیکونی) که به ویژه در کاربردهای کمولتاژ، کارایی کلی را کاهش میدهد.
تلفات حرارتی: اجزای توان مانند رگولاتورها و دیودها گرما تولید میکنند و بدون مدیریت حرارتی مناسب، عملکرد ممکن است کاهش یابد یا اجزا خراب شوند.
چالشهای طراحی و اقتصادی
اندازه و وزن در سطوح توان بالا: مبدلهای پرتوان به اجزای بزرگی مانند ترانسفورماتورها یا خازنها نیاز دارند که اندازه و وزن سیستم را افزایش میدهد.
هزینه اجزای پیشرفته: در حالی که استفاده از نیمههادیهای مدرن مانند GaN یا SiC عملکرد را بهبود میبخشد، هزینه طراحی و تولید را به طور قابل توجهی افزایش میدهد.
نیازمندیهای کنترل پیچیده: مبدلهای AC/DC هوشمند یا دیجیتال اغلب به الگوریتمهای کنترل دقیق و میکروکنترلرها نیاز دارند که سیستم را برای طراحی و نگهداری پیچیدهتر میکند.
تبدیل جریان متناوب به جریان مستقیم نمایانگر یکی از ارکان اساسی مهندسی برق مدرن است که عملکرد دستگاههای الکترونیکی و سیستمهای صنعتی بیشماری را ممکن میسازد. این تحقیق به طور سیستماتیک اصول بنیادی، مکانیسمهای عملیاتی و کاربردهای عملی تبدیل توان AC به DC را بررسی کرده است.
تحلیل جامع، مزایا و معایب متمایز هر دو منبع تغذیه AC و DC را آشکار ساخت و نقش مکمل آنها را در سیستمهای الکتریکی برجسته کرد. بررسی روشهای تبدیل خطی در مقابل سوئیچینگ، عملیبودن برتر تکنیکهای سوئیچینگ را به ویژه از نظر بهینهسازی اندازه ترانسفورماتور و کارایی کلی نشان داد.
علاوه بر این، کاوش سیستمهای قدرت سهفاز، از جمله پیکربندیهای ستاره و مثلث، بر مزیت قابل توجه آنها در ظرفیت انتقال توان در مقایسه با سیستمهای تکفاز تأکید کرد. بررسی دقیق مدارهای یکسوکننده، تکنیکهای تنظیم ولتاژ و معیارهای انتخاب قطعات، بینش ارزشمندی برای پیادهسازی عملی فراهم میکند.
با نگاه به آینده، زمینه تبدیل AC به DC با فناوریهای در حال ظهور و رویکردهای نوآورانه به تکامل خود ادامه میدهد. جهتهای تحقیقاتی آینده باید بر توسعه مواد نیمههادی پیشرفته، الگوریتمهای کنترل هوشمند و راهحلهای مدیریت توان یکپارچه برای پرداختن به چالشهای جاری در کارایی، مدیریت حرارتی و کوچکسازی سیستم متمرکز شود.
در اصل، این تحقیق به درک عمیقتری از فناوریهای تبدیل توان و نقش حیاتی آنها در پر کردن شکاف بین شبکههای توزیع توان AC و کاربردهای مبتنی بر DC کمک میکند و در نهایت از پیشرفت سیستمهای الکتریکی کارآمدتر و پایدارتر حمایت میکند.
https://www.sciencefacts.net/direct-current.html
https://www.monolithicpower.com/en/learning/resources/ac-dc-power-supply-basics
https://www.matsusada.com/column/dc_and_ac.html
https://eshop.se.com/in/blog/post/difference-between-active-power-reactive-power-and-apparent-power.html
https://en.wikipedia.org/wiki/Rectifier
https://pyspice.fabrice-salvaire.fr/releases/v1.4/examples/electricity/three-phase.html
https://www.build-electronic-circuits.com/linear-power-supply/
https://www.eleccircuit.com/what-switching-power-supply-how-does-it-work/
https://youtu.be/jsBn2r94BDA
https://youtu.be/JXJaRPXPwjQ
https://www.rohm.com/electronics-basics/ac-dc-converters/acdc_what1